Difference between revisions of "Elong-13-05-01"
| Line 36: | Line 36: | ||
Including the 1/2 term in the polarized cross-section (to stay consistent with HERMES' terminology), then <math>\delta A_{zz}^d = \frac{4}{P_{zz}\sqrt{f\cdot t\cdot R_{\mathrm{Total}}}}</math>. | Including the 1/2 term in the polarized cross-section (to stay consistent with HERMES' terminology), then <math>\delta A_{zz}^d = \frac{4}{P_{zz}\sqrt{f\cdot t\cdot R_{\mathrm{Total}}}}</math>. | ||
| − | Looking at two points in HERMES data, where <math>t\cdot R_{\mathrm{Total}} = 3.2\cdot 10^6</math> and <math>P_{zz} = 0.90</math>, I get:<br> | + | Looking at two points in HERMES data, where <math>R_{\mathrm{Total}} = R_{\mathrm{D}}</math>, <math>t\cdot R_{\mathrm{Total}} = 3.2\cdot 10^6</math>, and <math>P_{zz} = 0.90</math>, I get:<br> |
[[Image:2013-05-01-HERMES.png]] | [[Image:2013-05-01-HERMES.png]] | ||
| + | |||
| + | The lowest point in <math>\delta b_1^d</math> doesn't match because of the difference in <math>F_1^d</math> noted above, although I'm not sure why I get a smaller error on the highest point in <math>\delta A_{zz}</math>. | ||
Revision as of 15:04, 30 April 2013
Cross-Section Issue - Fixed
From looking at the dilution factor, f, I found a problem with how the cross-sections were calculated. We know that, naively,
<math>f=\frac{N_{D}}{(N_{D}+N_{N}+N_{He})} = \frac{t\cdot R_{D}}{(t\cdot R_{D}+t\cdot R_{N}+t\cdot R_{He})} = \frac{R_{D}}{(R_{D}+R_{N}+R_{He})} \approx \frac{N_{D}}{N_{D}+N_{N}}\approx \frac{3\sigma_{D}}{3\sigma_{D}+\sigma{N}}\approx \frac{3\cdot 2}{3\cdot 2 + 14}\approx 6/20=0.3</math>.
Originally, I was (wrongly) using
<math>\frac{d^2\sigma^u}{d\Omega dE'} = \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{X}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]</math>
where X = nucleus and <math>\left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}}=\frac{Z^2 \alpha^2 \hbar^2 c^2}{4E^2\sin^4\left( \frac{\theta}{2} \right)}\cos^2\left( \frac{\theta}{2} \right)</math>.
This gave <math>f \approx 0.062</math>.
The problem came from using a nuclear Mott cross-section but a nucleon structure cross-section. To fix this, I first found the Mott cross-section for a proton,
<math>\left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}}=\frac{1^2 \alpha^2 \hbar^2 c^2}{4E^2\sin^4\left( \frac{\theta}{2} \right)}\cos^2\left( \frac{\theta}{2} \right)</math>,
and then multiplied that by the structure cross-section at the total number of nucleons,
<math>\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{X}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]</math>.
This gave <math>f \approx \frac{3\sigma_{D}}{3\sigma_{D}+\sigma{N}} \approx 0.29</math>, as expected.
Plugging all this into the rates code gave:
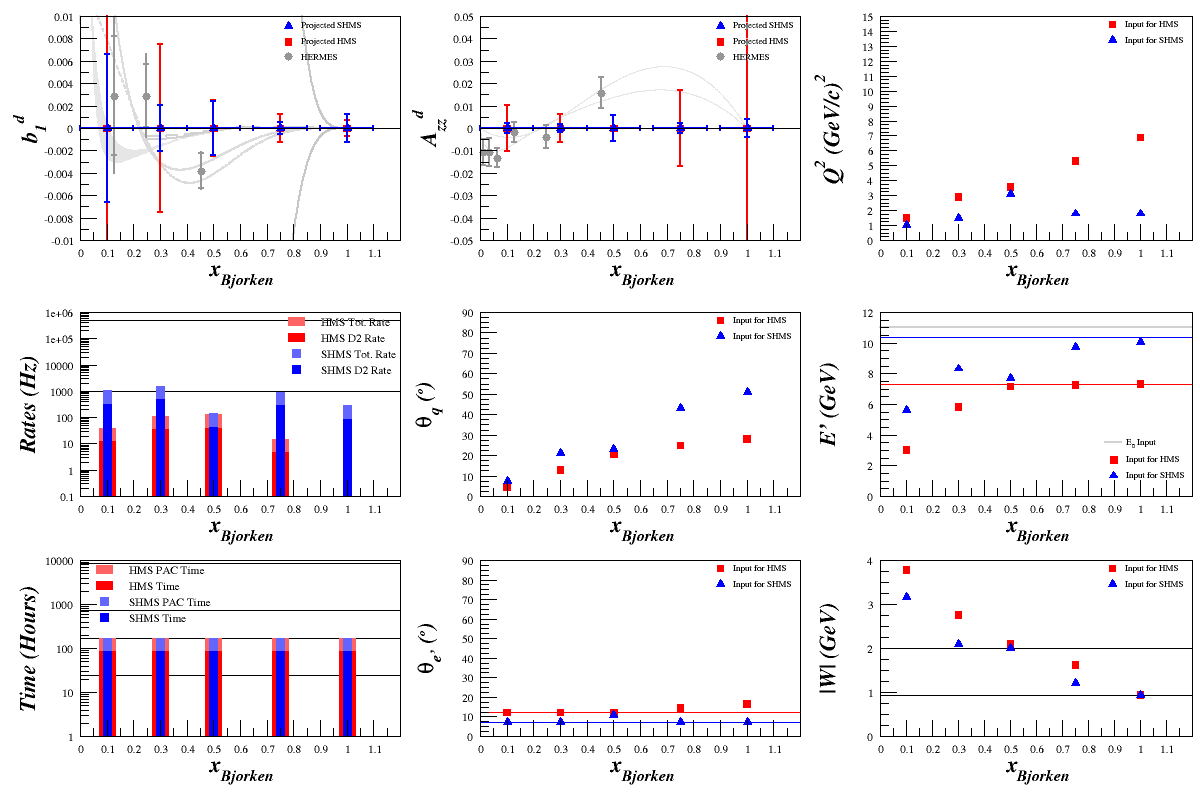
Matching HERMES <math>F_1^d</math>, <math>\delta A_{zz}^d</math>, and <math>\delta b_{1}^d</math>
I wanted to double-check the code against the HERMES data, but this required a few extra steps. First, using the values for <math>A_{zz}^d</math> and <math>b_{1}^d</math> that they measured, along with the formula <math>b_1^d = -\frac{3}{2}A^d_{zz}F^d_1</math>, I found what they were using for <math>F^d_1</math>. The <math>F^d_1</math> they're using is per nucleon, and for HERMES' two highest x points (the rest are inaccessible to the Bosted code because for 0.012<x<0.063, 16.75<W2<42.87, which is outside the W range that the code can handle) they match the code relatively well:
| <x> | Q 2 | HERMES <math>F_1^d</math> | Bosted <math>\frac{F_1^d}{A_d}</math> |
| 0.248 | 3.11 | 0.496 | 0.486 |
| 0.452 | 4.69 | 0.161 | 0.171 |
This means that the way I was calculating the error <math>\delta b_1^d=\frac{3}{2}\delta A_{zz}^d F_1^d</math> was off by a factor of <math>A_d=2</math>. This was corrected.
Including the 1/2 term in the polarized cross-section (to stay consistent with HERMES' terminology), then <math>\delta A_{zz}^d = \frac{4}{P_{zz}\sqrt{f\cdot t\cdot R_{\mathrm{Total}}}}</math>.
Looking at two points in HERMES data, where <math>R_{\mathrm{Total}} = R_{\mathrm{D}}</math>, <math>t\cdot R_{\mathrm{Total}} = 3.2\cdot 10^6</math>, and <math>P_{zz} = 0.90</math>, I get:
The lowest point in <math>\delta b_1^d</math> doesn't match because of the difference in <math>F_1^d</math> noted above, although I'm not sure why I get a smaller error on the highest point in <math>\delta A_{zz}</math>.
