Difference between revisions of "Elong-13-05-01-Azz-Method-2"
() |
|||
| (4 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
| style="width: 200px;" | Target Material = ND3 | | style="width: 200px;" | Target Material = ND3 | ||
|- | |- | ||
| − | | | + | | $z_{\mathrm{tgt}} = 3\mathrm{ cm}$ |
|- | |- | ||
| − | | | + | | $p_f = 0.65$ |
|- | |- | ||
| − | | | + | | $P_{zz} = 20\%$ |
|- | |- | ||
| − | | | + | | $N_{A} = 6.0221413\cdot 10^{23}$ |
|- | |- | ||
| − | | | + | | $\rho_{\mathrm{He}} = 0.1412 \mathrm{g/cm}^3$ |
|- | |- | ||
| − | | | + | | $M_{\mathrm{He}} = 4.0026 \mathrm{g/mole}$ |
|- | |- | ||
| − | | | + | | $\rho_{\mathrm{ND}_3} = 1.007 \mathrm{g/cm}^3$ |
|- | |- | ||
| − | | | + | | $M_{\mathrm{ND}_3} = 20 \mathrm{g/mole}$ |
|- | |- | ||
| − | | | + | | $I_{\mathrm{beam}} = 0.115 \mathrm{\mu A}$ |
|- | |- | ||
| − | | | + | | $\delta F_1^d = 5\%$ |
|- | |- | ||
|} | |} | ||
| Line 28: | Line 28: | ||
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(1) || | + | |style="width: 50px; height: 65px;" |(1) || $R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}}\left( \frac{d^2\sigma_{\mathrm{He}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{N}}\left( \frac{d^2\sigma_{\mathrm{N}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{D}}\left( \frac{d^2\sigma_{\mathrm{D}}}{d\Omega dE'}\right) \right]$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(2) || | + | |style="width: 50px; height: 65px;" |(2) || $R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}}\left( \frac{d^2\sigma_{\mathrm{He}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{N}}\left( \frac{d^2\sigma_{\mathrm{N}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{D}}\left( \frac{d^2\sigma_{\mathrm{D}}^u}{d\Omega dE'}\left[ 1 + \frac{1}{2}P_{zz}A_{zz}^d \right]\right) \right] $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(2a) || | + | |style="width: 50px; height: 65px;" |(2a) || $R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz}A_{zz}^d \right) \right] $ |
|} | |} | ||
where <br> | where <br> | ||
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(3) || | + | |style="width: 50px; height: 65px;" |(3) || $\mathcal{A} = \left( \Delta\Omega \Delta E' \right)$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(4) || | + | |style="width: 50px; height: 65px;" |(4) || $\mathcal{L}_{\mathrm{He}} = \left[ \mathcal{N}_A \frac{\rho_{\mathrm{He}}}{M_{\mathrm{He}}}\left(1 - p_f\right) \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(5) || | + | |style="width: 50px; height: 65px;" |(5) || $\mathcal{L}_{\mathrm{N}} = \left[ \mathcal{N}_A \frac{\rho_{\mathrm{ND}_3}}{M_{\mathrm{ND}_3}} p_f \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(6) || | + | |style="width: 50px; height: 65px;" |(6) || $\mathcal{L}_{\mathrm{D}} = 3\left[ \mathcal{N}_A \frac{\rho_{\mathrm{ND}_3}}{M_{\mathrm{ND}_3}} p_f \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}$ |
|- | |- | ||
| − | |style="width: 50px; height: 85px;" |(7) || | + | |style="width: 50px; height: 85px;" |(7) || $\sigma^u_X = \frac{d^2\sigma^u_X}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(8) || | + | |style="width: 50px; height: 65px;" |(8) || $\left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}}=\frac{1^2 \alpha^2 \hbar^2 c^2}{4E^2\sin^4\left( \frac{\theta}{2} \right)}\cos^2\left( \frac{\theta}{2} \right)$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(9) || | + | |style="width: 50px; height: 65px;" |(9) || $\sigma_D = \frac{d^2\sigma_{\mathrm{D}}}{d\Omega dE'} = \frac{d^2\sigma_{\mathrm{D}}^u}{d\Omega dE'}\left[ 1 + \frac{1}{2}P_{zz}A_{zz}^d \right] $ |
|- | |- | ||
|} | |} | ||
| Line 55: | Line 55: | ||
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(10) || | + | |style="width: 50px; height: 65px;" |(10) || $N_{Pol} - N_{u} = R^{Pol}_{\mathrm{Total}}t^{Pol}_{\mathrm{Total}} - R^{u}_{\mathrm{Total}}t^{u}_{\mathrm{Total}} $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(11) || | + | |style="width: 50px; height: 65px;" |(11) || $N_{u} = R^{u}_{\mathrm{Total}}t^{u}_{\mathrm{Total}} $ |
|- | |- | ||
|} | |} | ||
| − | If we assume that | + | If we assume that $t^{Pol}_{\mathrm{Total}} \approx t^{u}_{\mathrm{Total}} \approx t$, then |
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(12) || | + | |style="width: 50px; height: 65px;" |(12) || $N_{Pol} - N_{u} = \left( R^{Pol}_{\mathrm{Total}} - R^{u}_{\mathrm{Total}}\right) t $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(13) || | + | |style="width: 50px; height: 65px;" |(13) || $N_{Pol} - N_{u} = \left( \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz} A_{zz}^d \right) \right] - \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u \right] \right) t $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(13a) || | + | |style="width: 50px; height: 65px;" |(13a) || $N_{Pol} - N_{u} = \left( \mathcal{A}\mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u \left( \frac{1}{2}P_{zz} A_{zz} \right) \right) t$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(14) || | + | |style="width: 50px; height: 65px;" |(14) || $N_{u} = R^{u}_{\mathrm{Total}}t $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(15) || | + | |style="width: 50px; height: 65px;" |(15) || $N_{u} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u \right]t $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(16) || | + | |style="width: 50px; height: 65px;" |(16) || $\frac{N_{Pol} - N_{u}}{N_{u}} = \left( \frac{\mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u}{ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u } \right) \frac{1}{2} A_{zz} P_{zz}$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(17) || | + | |style="width: 50px; height: 65px;" |(17) || $\frac{N_{Pol} - N_{u}}{N_{u}} = f \frac{1}{2} A_{zz} P_{zz}$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(18) || | + | |style="width: 50px; height: 65px;" |(18) || $A_{\mathrm{meas}}^{(2)} = \frac{N_{Pol} - N_{u}}{N_{u}}$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(18a) || | + | |style="width: 50px; height: 65px;" |(18a) || $A_{\mathrm{meas}}^{(2)} = f \frac{1}{2} A_{zz} P_{zz}$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(19) || | + | |style="width: 50px; height: 65px;" |(19) || $A_{zz} = \frac{2 }{f \cdot P_{zz}}A_{\mathrm{meas}}^{(2)}$ |
|- | |- | ||
|} | |} | ||
| Line 89: | Line 89: | ||
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(20) || | + | |style="width: 50px; height: 65px;" |(20) || $\delta A_{zz} = \sqrt{\left( \frac{\partial A_{zz}}{\partial A_{\mathrm{meas}}^{(2)}} \delta A_{\mathrm{meas}}^{(2)} \right)^2 + \left( \frac{\partial A_{zz}}{\partial f} \delta f \right)^2 + \left( \frac{\partial A_{zz}}{\partial P_{zz}} \delta P_{zz} \right)^2 }$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(20a) || | + | |style="width: 50px; height: 65px;" |(20a) || $\delta A_{zz} = \sqrt{\left( \delta A_{zz}^{\mathrm{Stat}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Dil}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Pol}} \right) ^2 }$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(20b) || | + | |style="width: 50px; height: 65px;" |(20b) || $\delta A_{zz} = \sqrt{\left( \delta A_{zz}^{\mathrm{Stat}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Sys}} \right) ^2 }$ |
|- | |- | ||
|} | |} | ||
| − | Ignoring | + | Ignoring $\delta A_{zz}^{\mathrm{Sys}}$ for now (and in all of the plots I'm showing), then |
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(21) || | + | |style="width: 50px; height: 65px;" |(21) || $ \delta A_{zz}^{\mathrm{Stat}} = \frac{\partial A_{zz}}{\partial A_{\mathrm{meas}}^{(2)}} \delta A_{\mathrm{meas}}^{(2)} = \frac{2}{f\cdot P_{zz}} \delta A_{\mathrm{meas}}^{(2)} $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(22) || | + | |style="width: 50px; height: 65px;" |(22) || $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \left( \frac{\partial A_{\mathrm{meas}}^{(2)}}{\partial N_{Pol}} \delta N_{Pol} \right)^2 + \left( \frac{\partial A_{\mathrm{meas}}^{(2)}}{\partial N_{u}} \delta N_{u} \right)^2 }$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(23) || | + | |style="width: 50px; height: 65px;" |(23) || $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \left( \frac{1}{N_u} \sqrt{N_{Pol}} \right)^2 + \left( -\frac{N_{Pol}}{N_u^2} \sqrt{N_u} \right)^2 }$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(24) || | + | |style="width: 50px; height: 65px;" |(24) || $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \frac{N_{Pol}}{N_u^2} + \frac{N_{Pol}^2}{N_u^3} }$ |
|- | |- | ||
|} | |} | ||
| − | If we assume that | + | If we assume that $N_{Pol} \approx N_u \approx \frac{N}{2}$, then |
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(25) || | + | |style="width: 50px; height: 65px;" |(25) || $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \frac{N/2}{N^2/4} + \frac{N^2/4}{N^3/8} }$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(25a) || | + | |style="width: 50px; height: 65px;" |(25a) || $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \frac{2}{N} + \frac{2}{N} }$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(25b) || | + | |style="width: 50px; height: 65px;" |(25b) || $ \delta A_{\mathrm{meas}}^{(2)} = \frac{2}{\sqrt{N}}$ |
|- | |- | ||
|} | |} | ||
| Line 124: | Line 124: | ||
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(26) || | + | |style="width: 50px; height: 65px;" |(26) || $ \delta A_{zz}^{\mathrm{Stat}} = \frac{2}{f\cdot P_{zz}} \delta A_{\mathrm{meas}}^{(2)} $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(26a) || | + | |style="width: 50px; height: 65px;" |(26a) || $ \delta A_{zz}^{\mathrm{Stat}} = \frac{2}{f\cdot P_{zz}} \left( \frac{2}{\sqrt{N}} \right) $ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(27) || | + | |style="width: 50px; height: 65px;" |(27) || $ \delta A_{zz}^{\mathrm{Stat}} = \frac{4}{f\cdot P_{zz}\sqrt{t\cdot R_{\mathrm{Total}}}} $ |
|- | |- | ||
|} | |} | ||
| − | Using the same formalism that HERMES used (which defines | + | Using the same formalism that HERMES used (which defines $F_{1_{\mathrm{HERMES}}}^d = \frac{(1 + Q^2/\nu^2)F_2^d}{2x(1+R)}$ with $F_2^d=\frac{F_2^p + F_2^n}{2}$ as a ''per nucleon'' quantity, which corresponds to the Bosted that uses ''per nucleus'' by $F_{1_{\mathrm{HERMES}}}^d = \frac{F_{1_{\mathrm{Bosted}}}^d}{A_{\mathrm{D}}} = \frac{F_1^d}{2}$ -- [[Elong-13-05-01#Matching_HERMES_F1d.2C_dAzzd.2C_and_db1d|as described previously]]), we can extract $b_1^d$ and its uncertainty by |
{| class="wikitable" style="text-align:center; width:800px;" border="0" | {| class="wikitable" style="text-align:center; width:800px;" border="0" | ||
| − | |style="width: 50px; height: 65px;" |(18) || | + | |style="width: 50px; height: 65px;" |(18) || $ b_1^d = - \frac{3}{2}A_{zz} \left( \frac{F_1^d}{A_{\mathrm{D}}} \right)= - \frac{3}{2}A_{zz} \left( \frac{F_1^d}{2} \right)$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(19) || | + | |style="width: 50px; height: 65px;" |(19) || $ \delta b_1^d =\sqrt{ \left(\frac{\partial b_1^d}{\partial A_{zz}} \delta A_{zz} \right)^2 + \left(\frac{\partial b_1^d}{\partial F_1^d} \delta F_1^d \right)^2 }$ |
|- | |- | ||
| − | |style="width: 50px; height: 65px;" |(19a) || | + | |style="width: 50px; height: 65px;" |(19a) || $ \delta b_1^d =\sqrt{ \left[ - \frac{3}{2} \left( \frac{F_1^d}{2} \right)\delta A_{zz} \right]^2 + \left[ - \frac{3}{2} A_{zz} \left( \frac{1}{2} \right)\delta F_1^d \right]^2 }$ |
|- | |- | ||
|} | |} | ||
| Line 153: | Line 153: | ||
[[Image: 2013-05-02-total-rates.png]] | [[Image: 2013-05-02-total-rates.png]] | ||
| − | ==F1 from PDFs== | + | ==Comparing F1 from PDFs and Bosted== |
| + | '''Note: For the plots below, Phys Rate = D2 Rate Only''' | ||
| + | |||
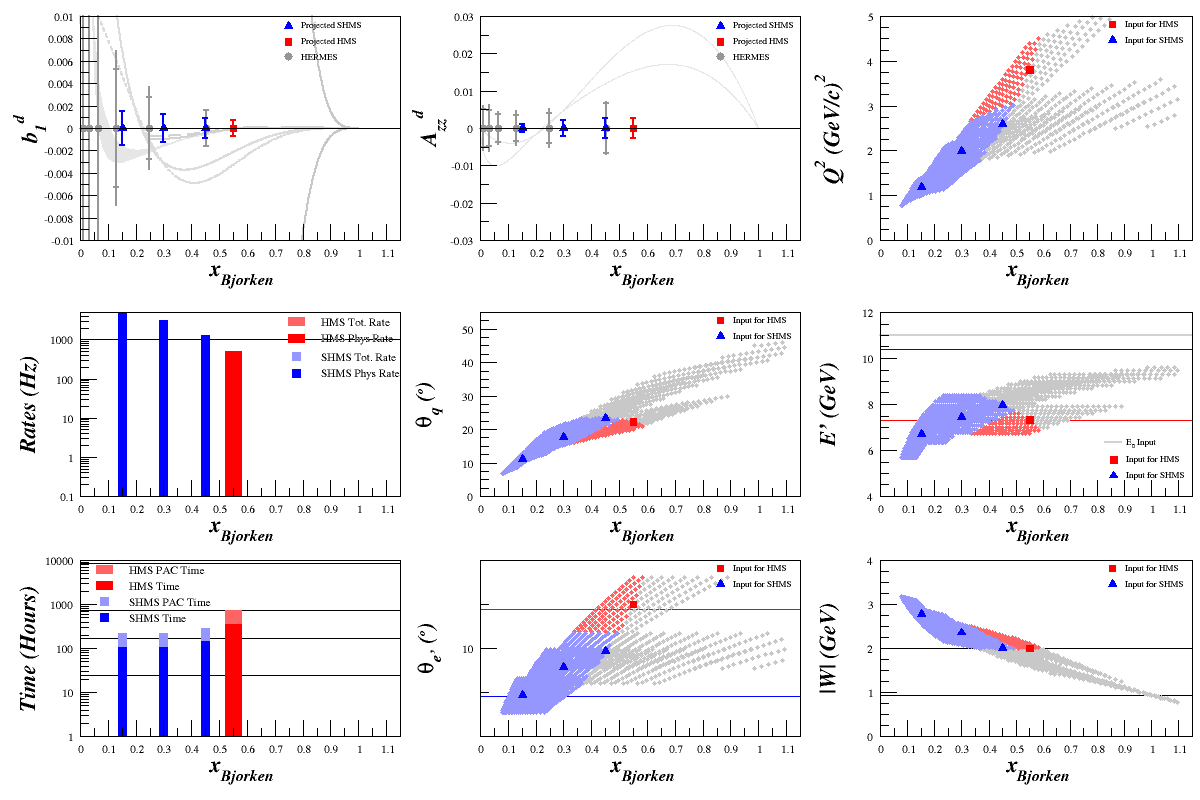
The plot below uses F1 calculated per nucleon from the PDF code, not from the Bosted code. | The plot below uses F1 calculated per nucleon from the PDF code, not from the Bosted code. | ||
[[Image: 2013-05-02-pdf-f1.png]] | [[Image: 2013-05-02-pdf-f1.png]] | ||
| + | |||
| + | If I calculate F1 per nucleon from the Bosted code, I get: | ||
| + | |||
| + | |||
| + | [[Image: 2013-05-02-bosted-f1.png]] | ||
| + | |||
| + | ==Removed arbitrary x cuts== | ||
| + | |||
| + | Removing arbitrary cuts on x, which were being used previously, increased the rate we can take at each point. Current estimates, where Phys Rate = D2 + N + He rates, are: | ||
| + | |||
| + | [[Image: 2013-05-02-remove-x-cuts.png]] | ||
| + | |||
| + | |||
| + | --[[User:Ellie|E. Long]] 20:59, 3 May 2013 (UTC) | ||
Latest revision as of 13:50, 18 October 2023
Azz Formalism - Method 2
Target Material = ND3 $z_{\mathrm{tgt}} = 3\mathrm{ cm}$ $p_f = 0.65$ $P_{zz} = 20\%$ $N_{A} = 6.0221413\cdot 10^{23}$ $\rho_{\mathrm{He}} = 0.1412 \mathrm{g/cm}^3$ $M_{\mathrm{He}} = 4.0026 \mathrm{g/mole}$ $\rho_{\mathrm{ND}_3} = 1.007 \mathrm{g/cm}^3$ $M_{\mathrm{ND}_3} = 20 \mathrm{g/mole}$ $I_{\mathrm{beam}} = 0.115 \mathrm{\mu A}$ $\delta F_1^d = 5\%$
| (1) | $R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}}\left( \frac{d^2\sigma_{\mathrm{He}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{N}}\left( \frac{d^2\sigma_{\mathrm{N}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{D}}\left( \frac{d^2\sigma_{\mathrm{D}}}{d\Omega dE'}\right) \right]$ |
| (2) | $R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}}\left( \frac{d^2\sigma_{\mathrm{He}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{N}}\left( \frac{d^2\sigma_{\mathrm{N}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{D}}\left( \frac{d^2\sigma_{\mathrm{D}}^u}{d\Omega dE'}\left[ 1 + \frac{1}{2}P_{zz}A_{zz}^d \right]\right) \right] $ |
| (2a) | $R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz}A_{zz}^d \right) \right] $ |
where
| (3) | $\mathcal{A} = \left( \Delta\Omega \Delta E' \right)$ |
| (4) | $\mathcal{L}_{\mathrm{He}} = \left[ \mathcal{N}_A \frac{\rho_{\mathrm{He}}}{M_{\mathrm{He}}}\left(1 - p_f\right) \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}$ |
| (5) | $\mathcal{L}_{\mathrm{N}} = \left[ \mathcal{N}_A \frac{\rho_{\mathrm{ND}_3}}{M_{\mathrm{ND}_3}} p_f \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}$ |
| (6) | $\mathcal{L}_{\mathrm{D}} = 3\left[ \mathcal{N}_A \frac{\rho_{\mathrm{ND}_3}}{M_{\mathrm{ND}_3}} p_f \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}$ |
| (7) | $\sigma^u_X = \frac{d^2\sigma^u_X}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]$ |
| (8) | $\left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}}=\frac{1^2 \alpha^2 \hbar^2 c^2}{4E^2\sin^4\left( \frac{\theta}{2} \right)}\cos^2\left( \frac{\theta}{2} \right)$ |
| (9) | $\sigma_D = \frac{d^2\sigma_{\mathrm{D}}}{d\Omega dE'} = \frac{d^2\sigma_{\mathrm{D}}^u}{d\Omega dE'}\left[ 1 + \frac{1}{2}P_{zz}A_{zz}^d \right] $ |
Then
| (10) | $N_{Pol} - N_{u} = R^{Pol}_{\mathrm{Total}}t^{Pol}_{\mathrm{Total}} - R^{u}_{\mathrm{Total}}t^{u}_{\mathrm{Total}} $ |
| (11) | $N_{u} = R^{u}_{\mathrm{Total}}t^{u}_{\mathrm{Total}} $ |
If we assume that $t^{Pol}_{\mathrm{Total}} \approx t^{u}_{\mathrm{Total}} \approx t$, then
| (12) | $N_{Pol} - N_{u} = \left( R^{Pol}_{\mathrm{Total}} - R^{u}_{\mathrm{Total}}\right) t $ |
| (13) | $N_{Pol} - N_{u} = \left( \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz} A_{zz}^d \right) \right] - \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u \right] \right) t $ |
| (13a) | $N_{Pol} - N_{u} = \left( \mathcal{A}\mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u \left( \frac{1}{2}P_{zz} A_{zz} \right) \right) t$ |
| (14) | $N_{u} = R^{u}_{\mathrm{Total}}t $ |
| (15) | $N_{u} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u \right]t $ |
| (16) | $\frac{N_{Pol} - N_{u}}{N_{u}} = \left( \frac{\mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u}{ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u } \right) \frac{1}{2} A_{zz} P_{zz}$ |
| (17) | $\frac{N_{Pol} - N_{u}}{N_{u}} = f \frac{1}{2} A_{zz} P_{zz}$ |
| (18) | $A_{\mathrm{meas}}^{(2)} = \frac{N_{Pol} - N_{u}}{N_{u}}$ |
| (18a) | $A_{\mathrm{meas}}^{(2)} = f \frac{1}{2} A_{zz} P_{zz}$ |
| (19) | $A_{zz} = \frac{2 }{f \cdot P_{zz}}A_{\mathrm{meas}}^{(2)}$ |
In order to get the uncertainty, we'd use
| (20) | $\delta A_{zz} = \sqrt{\left( \frac{\partial A_{zz}}{\partial A_{\mathrm{meas}}^{(2)}} \delta A_{\mathrm{meas}}^{(2)} \right)^2 + \left( \frac{\partial A_{zz}}{\partial f} \delta f \right)^2 + \left( \frac{\partial A_{zz}}{\partial P_{zz}} \delta P_{zz} \right)^2 }$ |
| (20a) | $\delta A_{zz} = \sqrt{\left( \delta A_{zz}^{\mathrm{Stat}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Dil}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Pol}} \right) ^2 }$ |
| (20b) | $\delta A_{zz} = \sqrt{\left( \delta A_{zz}^{\mathrm{Stat}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Sys}} \right) ^2 }$ |
Ignoring $\delta A_{zz}^{\mathrm{Sys}}$ for now (and in all of the plots I'm showing), then
| (21) | $ \delta A_{zz}^{\mathrm{Stat}} = \frac{\partial A_{zz}}{\partial A_{\mathrm{meas}}^{(2)}} \delta A_{\mathrm{meas}}^{(2)} = \frac{2}{f\cdot P_{zz}} \delta A_{\mathrm{meas}}^{(2)} $ |
| (22) | $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \left( \frac{\partial A_{\mathrm{meas}}^{(2)}}{\partial N_{Pol}} \delta N_{Pol} \right)^2 + \left( \frac{\partial A_{\mathrm{meas}}^{(2)}}{\partial N_{u}} \delta N_{u} \right)^2 }$ |
| (23) | $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \left( \frac{1}{N_u} \sqrt{N_{Pol}} \right)^2 + \left( -\frac{N_{Pol}}{N_u^2} \sqrt{N_u} \right)^2 }$ |
| (24) | $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \frac{N_{Pol}}{N_u^2} + \frac{N_{Pol}^2}{N_u^3} }$ |
If we assume that $N_{Pol} \approx N_u \approx \frac{N}{2}$, then
| (25) | $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \frac{N/2}{N^2/4} + \frac{N^2/4}{N^3/8} }$ |
| (25a) | $ \delta A_{\mathrm{meas}}^{(2)} = \sqrt{ \frac{2}{N} + \frac{2}{N} }$ |
| (25b) | $ \delta A_{\mathrm{meas}}^{(2)} = \frac{2}{\sqrt{N}}$ |
which would yield
| (26) | $ \delta A_{zz}^{\mathrm{Stat}} = \frac{2}{f\cdot P_{zz}} \delta A_{\mathrm{meas}}^{(2)} $ |
| (26a) | $ \delta A_{zz}^{\mathrm{Stat}} = \frac{2}{f\cdot P_{zz}} \left( \frac{2}{\sqrt{N}} \right) $ |
| (27) | $ \delta A_{zz}^{\mathrm{Stat}} = \frac{4}{f\cdot P_{zz}\sqrt{t\cdot R_{\mathrm{Total}}}} $ |
Using the same formalism that HERMES used (which defines $F_{1_{\mathrm{HERMES}}}^d = \frac{(1 + Q^2/\nu^2)F_2^d}{2x(1+R)}$ with $F_2^d=\frac{F_2^p + F_2^n}{2}$ as a per nucleon quantity, which corresponds to the Bosted that uses per nucleus by $F_{1_{\mathrm{HERMES}}}^d = \frac{F_{1_{\mathrm{Bosted}}}^d}{A_{\mathrm{D}}} = \frac{F_1^d}{2}$ -- as described previously), we can extract $b_1^d$ and its uncertainty by
| (18) | $ b_1^d = - \frac{3}{2}A_{zz} \left( \frac{F_1^d}{A_{\mathrm{D}}} \right)= - \frac{3}{2}A_{zz} \left( \frac{F_1^d}{2} \right)$ |
| (19) | $ \delta b_1^d =\sqrt{ \left(\frac{\partial b_1^d}{\partial A_{zz}} \delta A_{zz} \right)^2 + \left(\frac{\partial b_1^d}{\partial F_1^d} \delta F_1^d \right)^2 }$ |
| (19a) | $ \delta b_1^d =\sqrt{ \left[ - \frac{3}{2} \left( \frac{F_1^d}{2} \right)\delta A_{zz} \right]^2 + \left[ - \frac{3}{2} A_{zz} \left( \frac{1}{2} \right)\delta F_1^d \right]^2 }$ |
Plots with using Azz Method 2 Calculations
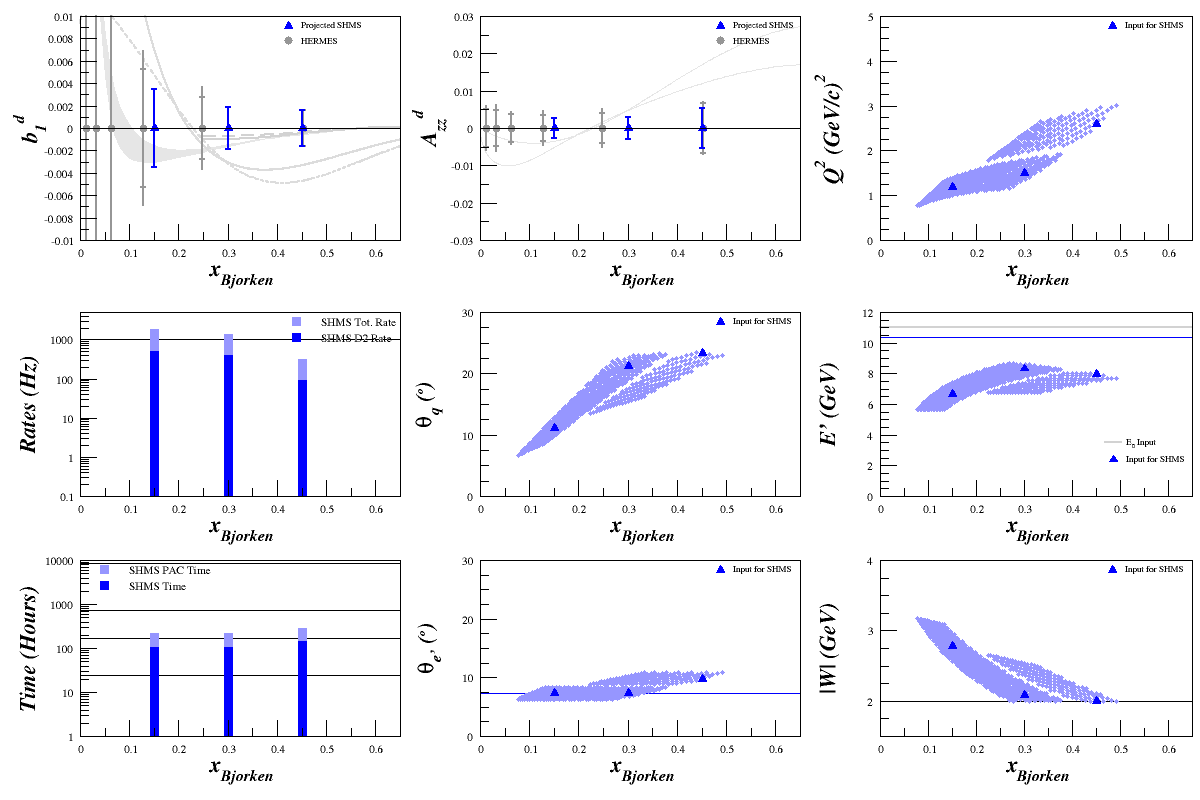
Total Rates
Ignoring our W>2 physics cut, then our total rates come out to:
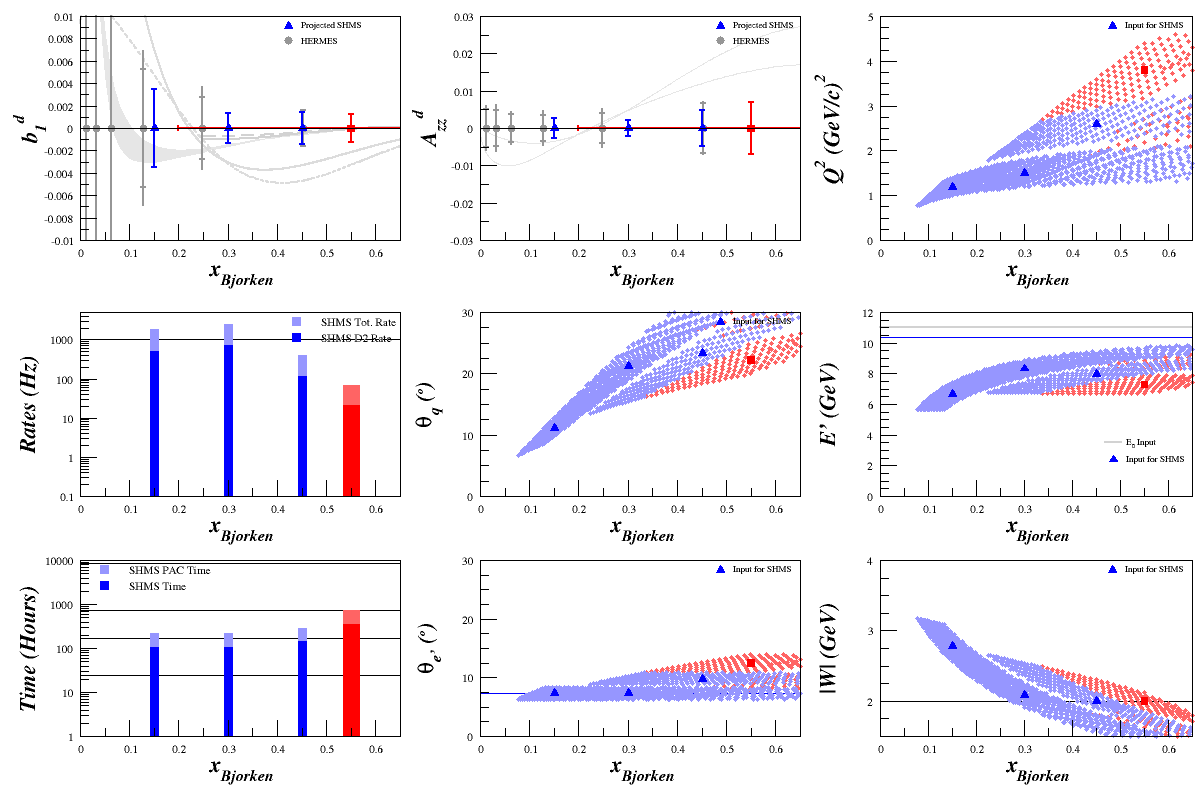
Comparing F1 from PDFs and Bosted
Note: For the plots below, Phys Rate = D2 Rate Only
The plot below uses F1 calculated per nucleon from the PDF code, not from the Bosted code.
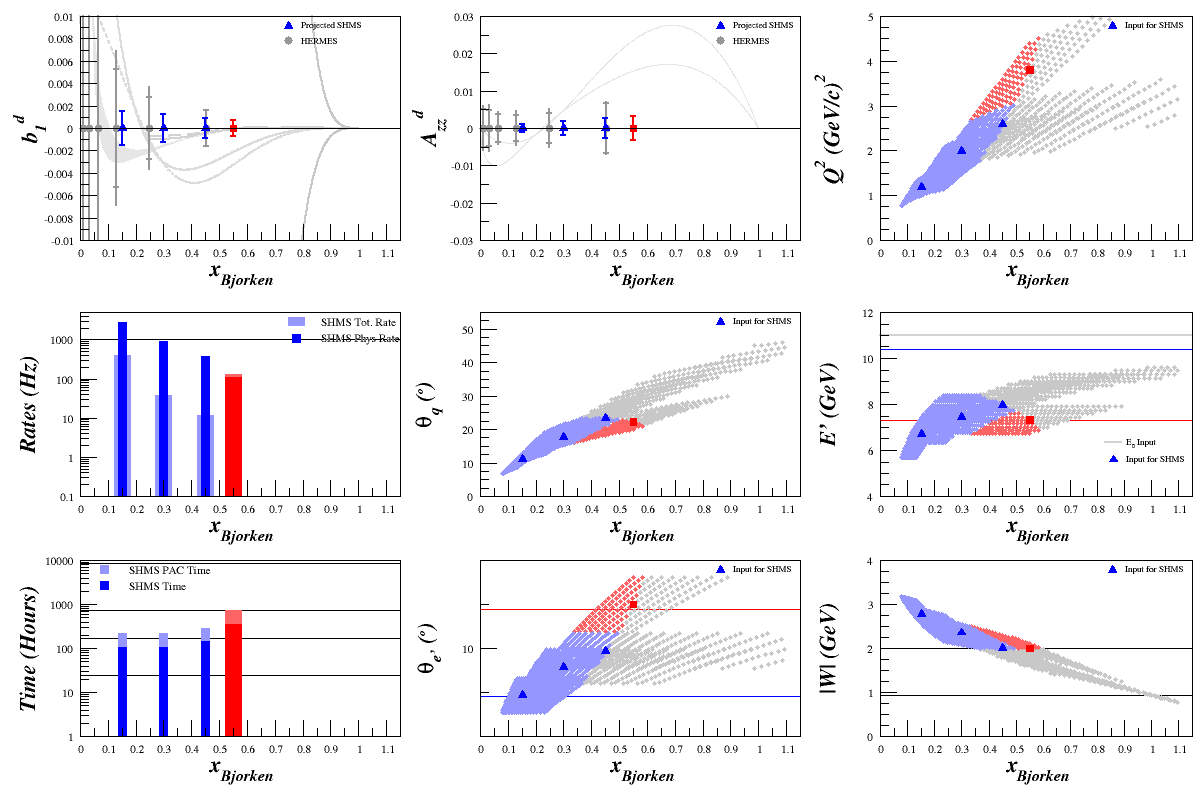
If I calculate F1 per nucleon from the Bosted code, I get:
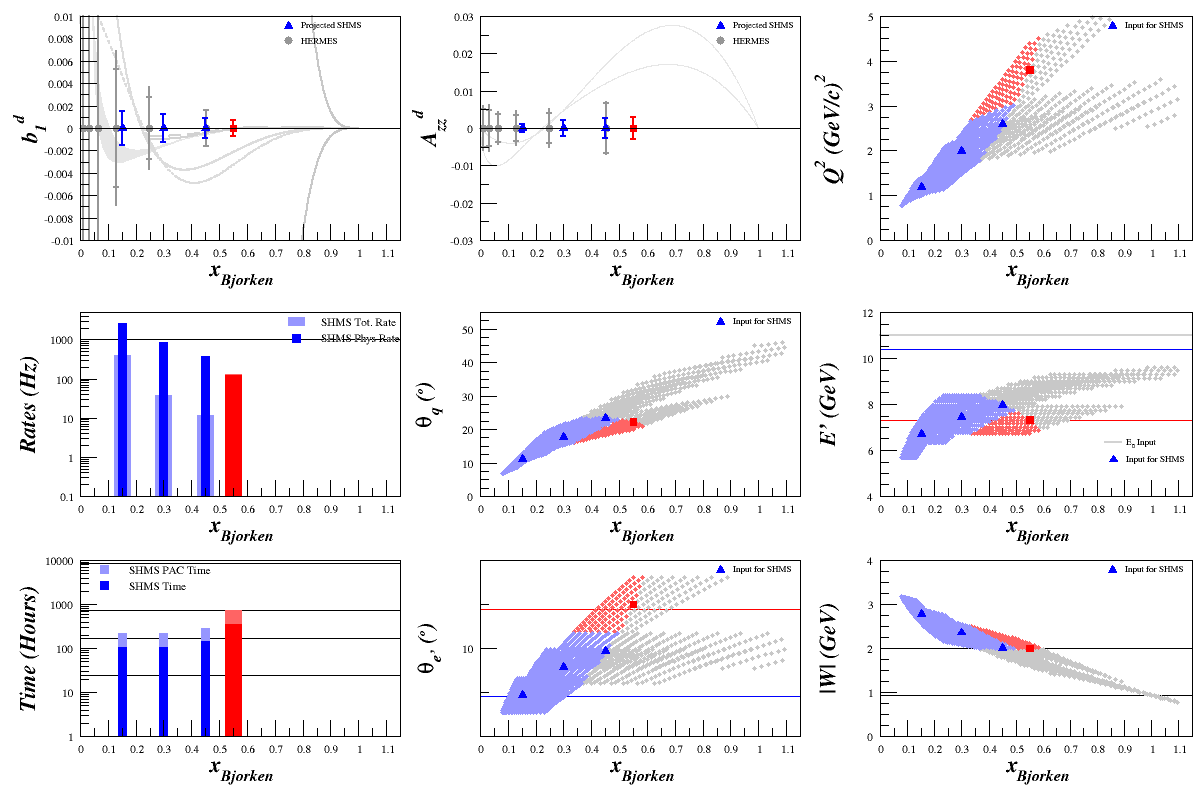
Removed arbitrary x cuts
Removing arbitrary cuts on x, which were being used previously, increased the rate we can take at each point. Current estimates, where Phys Rate = D2 + N + He rates, are:
--E. Long 20:59, 3 May 2013 (UTC)