Difference between revisions of "Elong-13-06-03"
| (7 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
::{| class="wikitable" style="text-align:center; border-collapse:collapse;" border="1" | ::{| class="wikitable" style="text-align:center; border-collapse:collapse;" border="1" | ||
| − | | style="width: 200px;" | | + | | style="width: 200px;" | $x_{\mathrm{Spectrometer}}$ || style="width: 200px;" | $dA_{zz}^{drift}$ |
|- | |- | ||
| 0.15 || 0.0046 | | 0.15 || 0.0046 | ||
| Line 16: | Line 16: | ||
|} | |} | ||
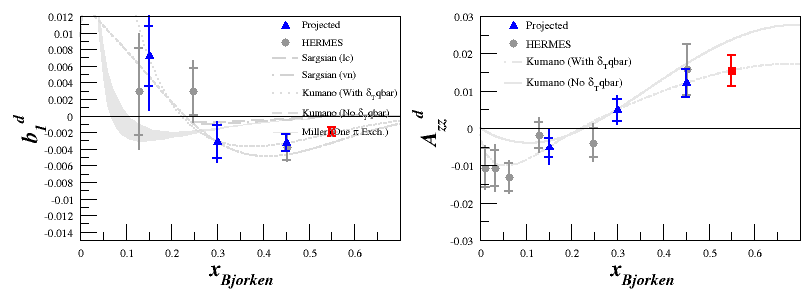
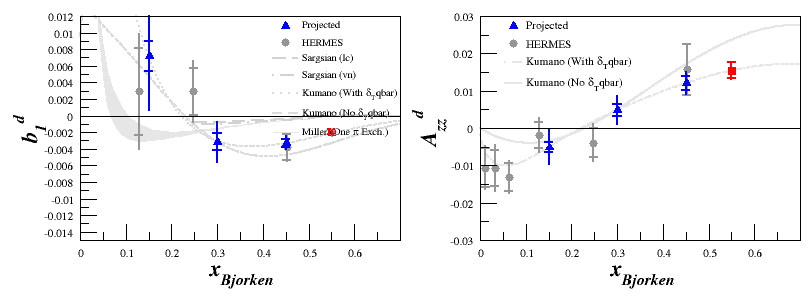
| − | For the spectrometer | + | For the plots using the spectrometer settings as bins, where $A_{zz}$ and $b_1$ are in blue and red, these are included as an additional systematic uncertainty. |
| + | |||
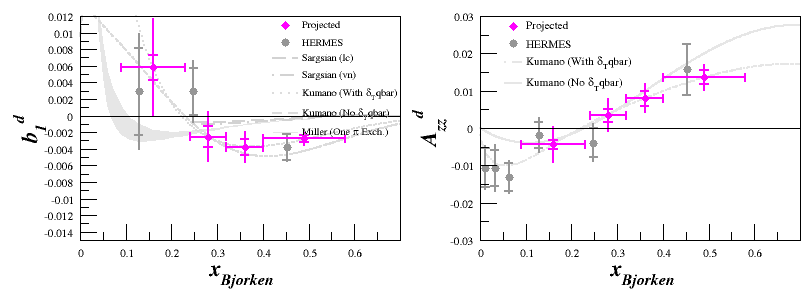
| + | For the rebinned plots, where $A_{zz}$ and $b_1$ are in pink, each of the drift uncertainties are added as a weighted average. The weights are the number of events that each spectrometer contributes to the rebinned statistics. | ||
| + | |||
| + | That's to say, | ||
| + | |||
| + | $dA_{zz}^{Ave. Drift} = \frac{\sum \left( dA_{zz}^{drift}N_{Spec} \right)}{N_{Total}}$ | ||
| + | |||
| + | where $dA_{zz}^{drift}$ is shown in the table above for each spectrometer setting, $N_{Spec}$ is the number of events from a particular spectrometer setting that go into this x bin, and $N_{Total}$ is the total number of events, from all spectrometer settings, that go into this x bin. | ||
==Conservative Estimates== | ==Conservative Estimates== | ||
| − | If we apply these with a conservative estimate, with | + | If we apply these with a conservative estimate, with $P_{zz}=20\%$ and $dA_{zz}^{(Rel. Sys)} = 12\%$, we can estimate both the full spectrometer bins: |
[[Image: 2013-06-03-spec-Pzz-20.png]] | [[Image: 2013-06-03-spec-Pzz-20.png]] | ||
| − | We can then use a weighted average for | + | We can then use a weighted average for $dA_{zz}^{drift}$, where the weights are number of events that each spectrometer setting contributes to a particular $x$ bin. The rebinned estimate is then: |
[[Image: 2013-06-03-Pzz-20.png]] | [[Image: 2013-06-03-Pzz-20.png]] | ||
| Line 34: | Line 42: | ||
==Optimistic Estimates== | ==Optimistic Estimates== | ||
| − | If we apply these with an optimistic estimate, with | + | If we apply these with an optimistic estimate, with $P_{zz}=40\%$ and $dA_{zz}^{(Rel. Sys)} = 6\%$, we can estimate both the full spectrometer bins: |
[[Image: 2013-06-03-spec-Pzz-40.png]] | [[Image: 2013-06-03-spec-Pzz-40.png]] | ||
| − | We can then use a weighted average for | + | We can then use a weighted average for $dA_{zz}^{drift}$, where the weights are number of events that each spectrometer setting contributes to a particular $x$ bin. The rebinned estimate is then: |
[[Image: 2013-06-03-Pzz-40.png]] | [[Image: 2013-06-03-Pzz-40.png]] | ||
Latest revision as of 13:53, 18 October 2023
Including Drift by Bin
Dustin's work on the drift has given a different value depending on the spectrometer setting, which are shown in the table below.
$x_{\mathrm{Spectrometer}}$ $dA_{zz}^{drift}$ 0.15 0.0046 0.30 0.0037 0.45 0.0028 0.55 0.0021
For the plots using the spectrometer settings as bins, where $A_{zz}$ and $b_1$ are in blue and red, these are included as an additional systematic uncertainty.
For the rebinned plots, where $A_{zz}$ and $b_1$ are in pink, each of the drift uncertainties are added as a weighted average. The weights are the number of events that each spectrometer contributes to the rebinned statistics.
That's to say,
$dA_{zz}^{Ave. Drift} = \frac{\sum \left( dA_{zz}^{drift}N_{Spec} \right)}{N_{Total}}$
where $dA_{zz}^{drift}$ is shown in the table above for each spectrometer setting, $N_{Spec}$ is the number of events from a particular spectrometer setting that go into this x bin, and $N_{Total}$ is the total number of events, from all spectrometer settings, that go into this x bin.
Conservative Estimates
If we apply these with a conservative estimate, with $P_{zz}=20\%$ and $dA_{zz}^{(Rel. Sys)} = 12\%$, we can estimate both the full spectrometer bins:
We can then use a weighted average for $dA_{zz}^{drift}$, where the weights are number of events that each spectrometer setting contributes to a particular $x$ bin. The rebinned estimate is then:
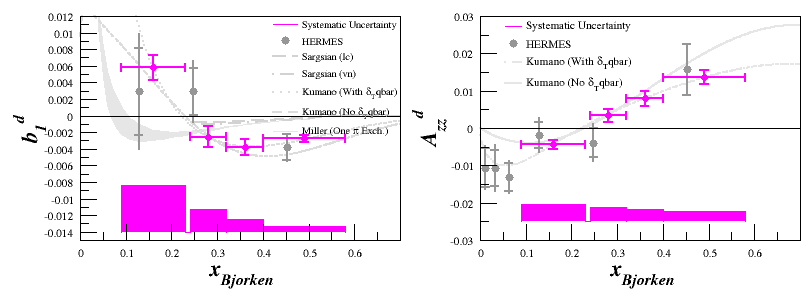
Same as above, but if we split the systematic uncertainty into bars, we get:
Optimistic Estimates
If we apply these with an optimistic estimate, with $P_{zz}=40\%$ and $dA_{zz}^{(Rel. Sys)} = 6\%$, we can estimate both the full spectrometer bins:
We can then use a weighted average for $dA_{zz}^{drift}$, where the weights are number of events that each spectrometer setting contributes to a particular $x$ bin. The rebinned estimate is then:
Same as above, but if we split the systematic uncertainty into bars, we get:
--E. Long 20:58, 3 June 2013 (UTC)