Difference between revisions of "Elong-14-05-09"
From HallCWiki
Jump to navigationJump to search| (6 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
Using the Frankfurt and Strikman equation 7.3, | Using the Frankfurt and Strikman equation 7.3, | ||
| − | + | $A_{zz} = R(p_s) = \frac{3(k_t^2/2-k_z^2)}{k^2}\frac{u(k)w(k)\sqrt{2}+\frac{1}{2}w^2(k)}{u^2(k)+w^2(k)}$ | |
| − | I'm trying to recreated their Figure 7.5. I don't entirely understand what | + | I'm trying to recreated their Figure 7.5. I don't entirely understand what $k_t$, $k_z$, and $k$ are, but if the ratio out front comes out to -3, I can recreate the D(e,e'p) at 180 degrees plot: |
[[Image:2014-05-09-fs-fig-7-3.png]] | [[Image:2014-05-09-fs-fig-7-3.png]] | ||
| Line 14: | Line 14: | ||
[[Image:2014-05-12-wavefunctions-without-fs.png]] | [[Image:2014-05-12-wavefunctions-without-fs.png]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 14:22, 18 October 2023
Recreating F&S Azz
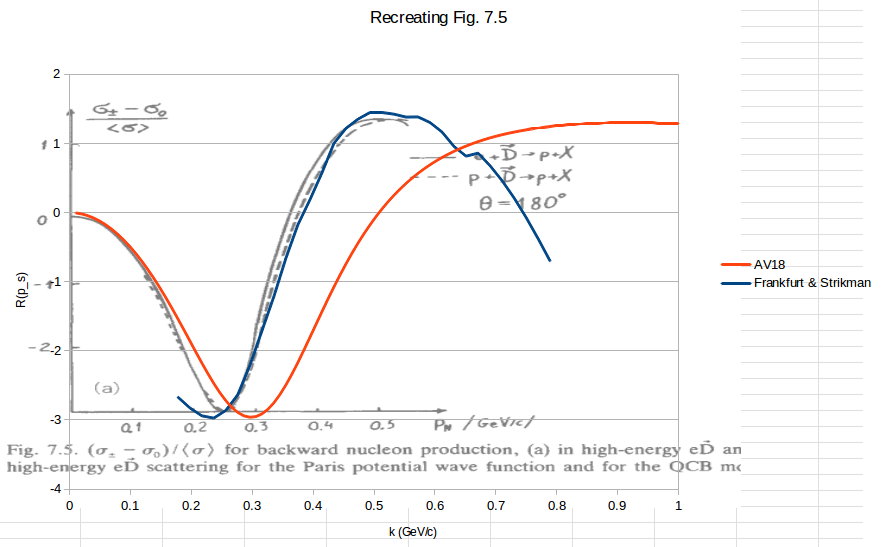
Using the Frankfurt and Strikman equation 7.3,
$A_{zz} = R(p_s) = \frac{3(k_t^2/2-k_z^2)}{k^2}\frac{u(k)w(k)\sqrt{2}+\frac{1}{2}w^2(k)}{u^2(k)+w^2(k)}$
I'm trying to recreated their Figure 7.5. I don't entirely understand what $k_t$, $k_z$, and $k$ are, but if the ratio out front comes out to -3, I can recreate the D(e,e'p) at 180 degrees plot:
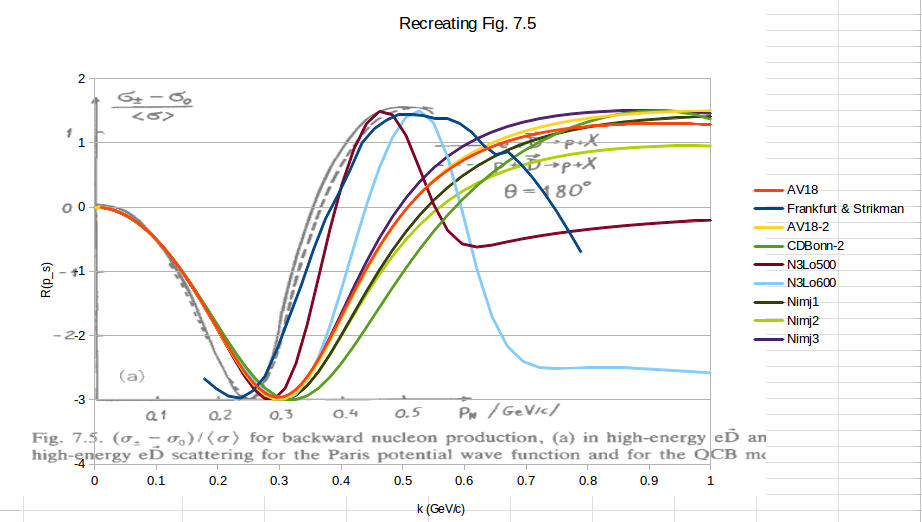
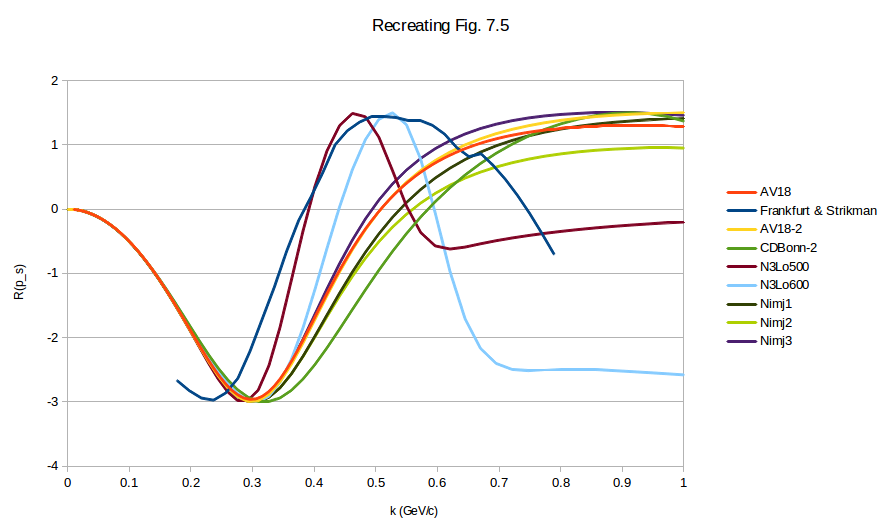
Repeating this same process for all of the wavefunctions that I received from Donal, making sure that the low-k part of the D-state wavefunction is positive as is their convention in Figure 7.1, we see