Difference between revisions of "Elong-15-03-26"
(→t20) |
|||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=11 GeV Beam= | =11 GeV Beam= | ||
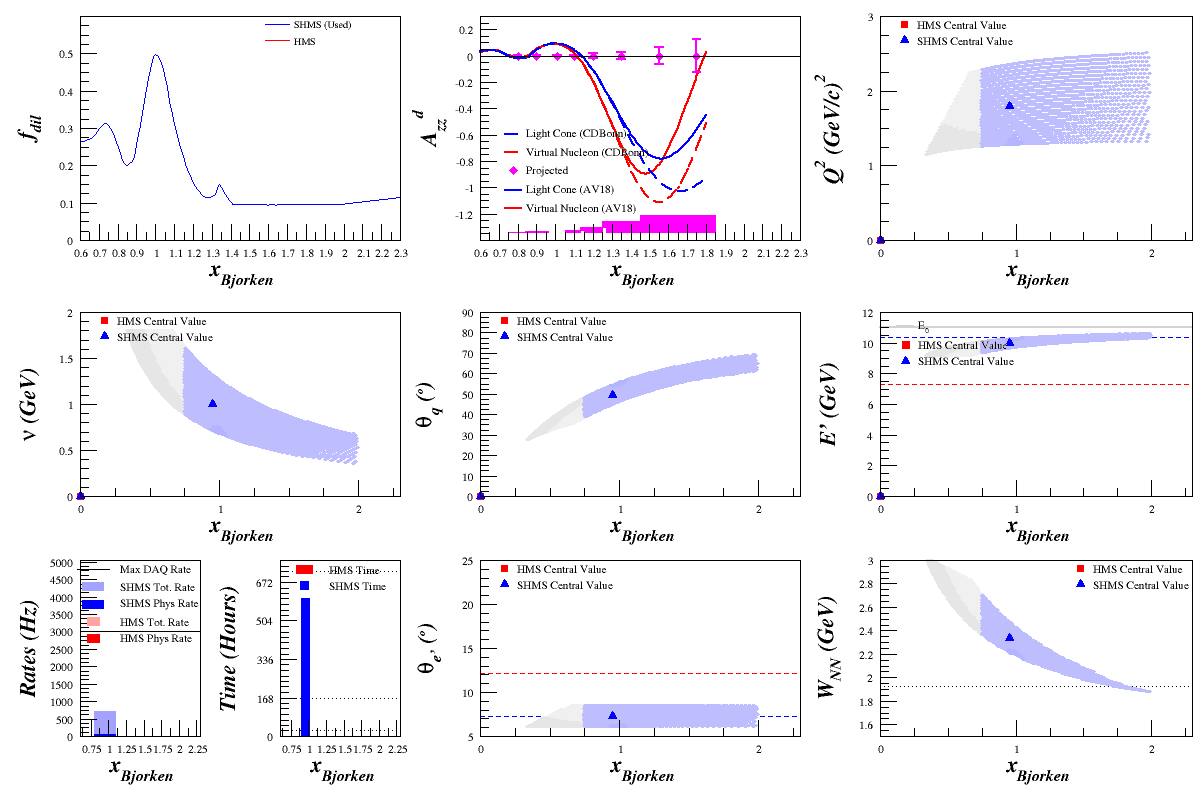
| − | Based on discussions with Mark and Gerry, I redid the rates using a differently-binned 11 GeV bin to increase nu and | + | Based on discussions with Mark and Gerry, I redid the rates using a differently-binned 11 GeV bin to increase nu and $W_{NN}^2= 2\nu m_D+m_D^2 -Q^2$, as there was concern about the curves not being valid for low nu~0.5 GeV. W was replaced with W_NN, and the dotted line shows $W_{NN}=m_D+50$ MeV. |
[[Image:2015-03-26-11gev.png]] | [[Image:2015-03-26-11gev.png]] | ||
| + | |||
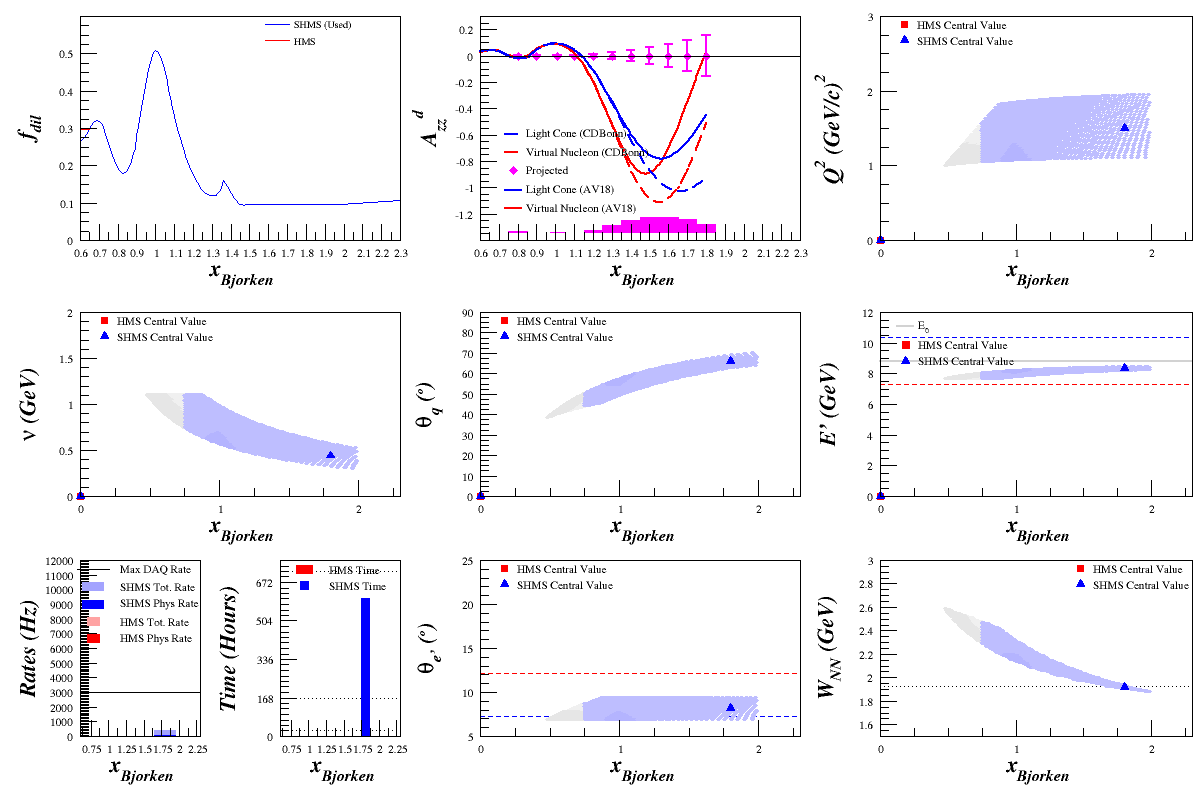
| + | =8.8 GeV Beam= | ||
| + | Compare the above to the calculations for an 8.8 GeV Beam, shown below. | ||
| + | |||
| + | [[Image:2015-04-27-88gev.png]] | ||
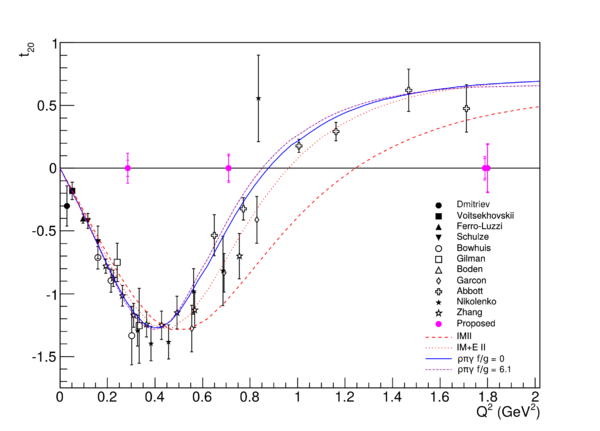
=t20= | =t20= | ||
| − | Using the Bosted code, I calculated first preliminary estimates for t20 using existing kinematics (although the 8.8 GeV kinematic was replaced with the above 11 GeV), utilizing 35 days of beam time. | + | Using the Bosted code, I calculated first preliminary estimates for t20 using existing Azz kinematics (although the 8.8 GeV kinematic was replaced with the above 11 GeV), utilizing 35 days of beam time. Bosted likely over-estimates statistics (see below), so take with a grain of salt. |
| + | |||
| + | '''[[Elong-15-04-07 | Note: Calculations below have been updated. Click here for more recent t20 results.]]''' | ||
[[Image:2015-03-26-t20.png|600px]] | [[Image:2015-03-26-t20.png|600px]] | ||
| Line 14: | Line 21: | ||
| − | [[Image:2015-03-26-ff-check.png|600px]] | + | [[Image:2015-03-26-ff-check.png|400px]] |
| + | |||
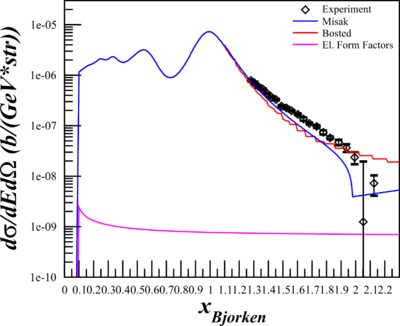
| + | I have also previously looked at another set of deuteron Shutz76 cross-section data at E_beam=11.671 GeV, theta=8 deg, Q^2~2.5 GeV^2, where Misak's code worked well. However, in the intervening months I've added a number of kinematic restrictions such that it won't calculate up to x=2 for t20, which I'm still looking to fix. | ||
| + | |||
| + | [[Image:2015-03-26-Shutz-11GeV-fdil.png|400px]] | ||
| + | |||
| + | =Azz for Systematics= | ||
| + | |||
| + | Zooming in on the area of small Azz, it looks like the smallest measurement we're expecting is ~1E-2, which I believe is an order of magnitude larger than where our current understanding of beam systematics is. | ||
| + | |||
| + | [[Image:2015-03-27-azz-zoom.png|600px]] | ||
Latest revision as of 14:29, 18 October 2023
11 GeV Beam
Based on discussions with Mark and Gerry, I redid the rates using a differently-binned 11 GeV bin to increase nu and $W_{NN}^2= 2\nu m_D+m_D^2 -Q^2$, as there was concern about the curves not being valid for low nu~0.5 GeV. W was replaced with W_NN, and the dotted line shows $W_{NN}=m_D+50$ MeV.
8.8 GeV Beam
Compare the above to the calculations for an 8.8 GeV Beam, shown below.
t20
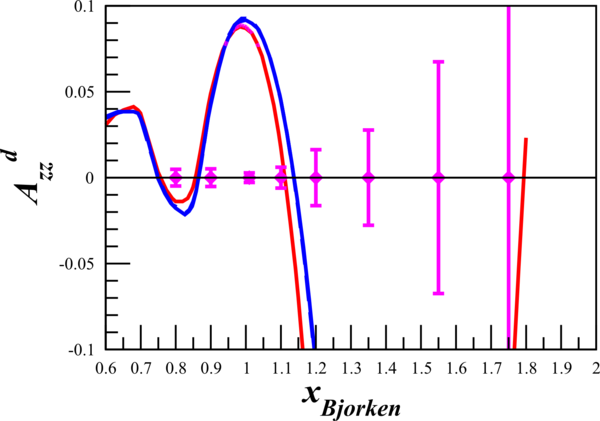
Using the Bosted code, I calculated first preliminary estimates for t20 using existing Azz kinematics (although the 8.8 GeV kinematic was replaced with the above 11 GeV), utilizing 35 days of beam time. Bosted likely over-estimates statistics (see below), so take with a grain of salt.
Note: Calculations below have been updated. Click here for more recent t20 results.
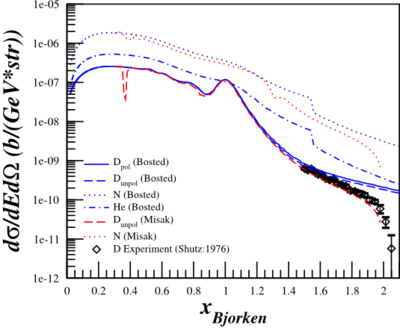
I had been working on the parameterization of the A and B form factors, but was having difficulty finding elastic cross section data to compare the results to. Looking at the Shutz76 data (E_beam=6.519 GeV, theta=8 deg, Q^2~0.8 GeV^2), the paramterized FFs were coming up orders of magnitude short from the data, whereas Bosted did a much better job.
I have also previously looked at another set of deuteron Shutz76 cross-section data at E_beam=11.671 GeV, theta=8 deg, Q^2~2.5 GeV^2, where Misak's code worked well. However, in the intervening months I've added a number of kinematic restrictions such that it won't calculate up to x=2 for t20, which I'm still looking to fix.
Azz for Systematics
Zooming in on the area of small Azz, it looks like the smallest measurement we're expecting is ~1E-2, which I believe is an order of magnitude larger than where our current understanding of beam systematics is.