Difference between revisions of "Elong-14-05-09"
| Line 37: | Line 37: | ||
[[Image:2014-05-15-rt0-current.png|600px]][[Image:2014-05-15-legend.png|75px]] | [[Image:2014-05-15-rt0-current.png|600px]][[Image:2014-05-15-legend.png|75px]] | ||
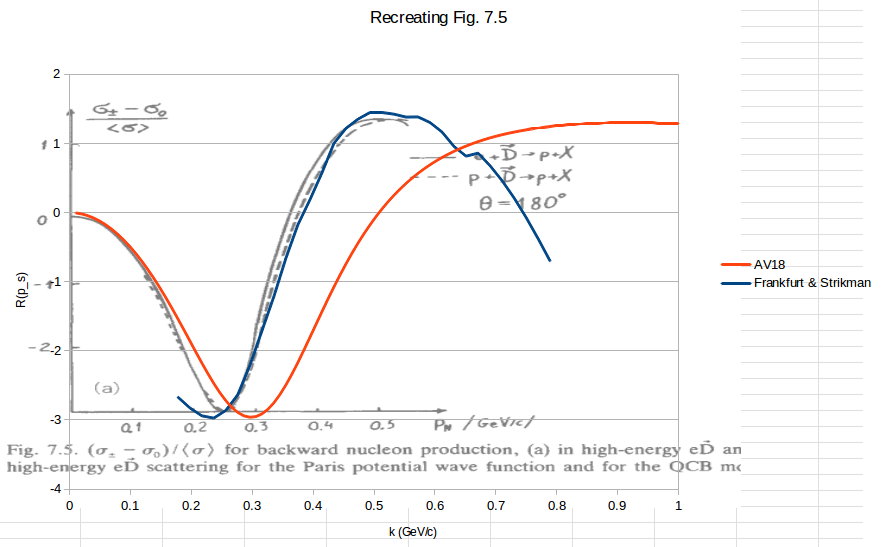
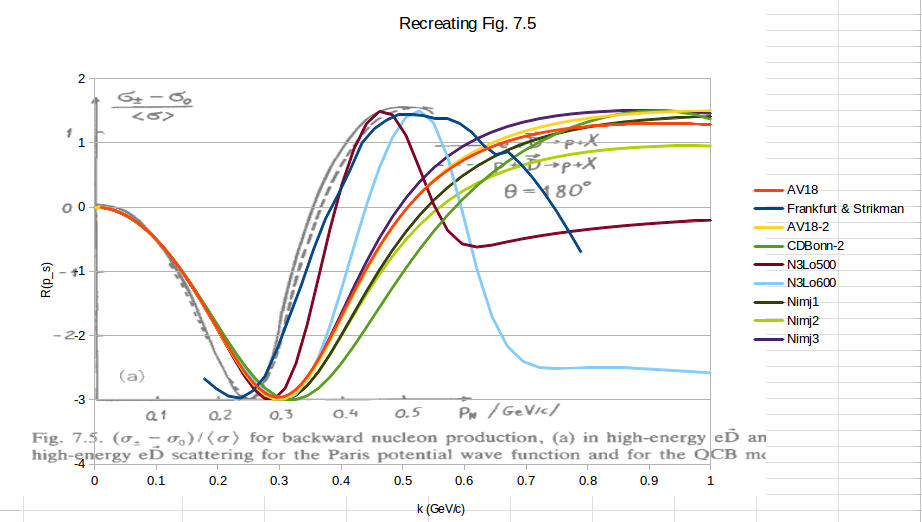
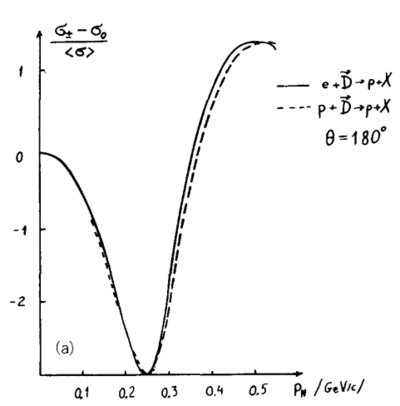
| − | This would make their Fig. 7.5 from [http://www.sciencedirect.com/science/article/pii/0370157388901792 their 1988 report] simply <math>A_{zz} = r(\pm 1,k)-r(0,k)</math>, which can also be | + | This would make their Fig. 7.5 from [http://www.sciencedirect.com/science/article/pii/0370157388901792 their 1988 report] simply <math>A_{zz} = r(\pm 1,k)-r(0,k)</math> for D(e,e'p) with p at 180deg, which can also be reproduced. |
[[Image:2014-05-15-fs-fig-7-5.png|400px]] | [[Image:2014-05-15-fs-fig-7-5.png|400px]] | ||
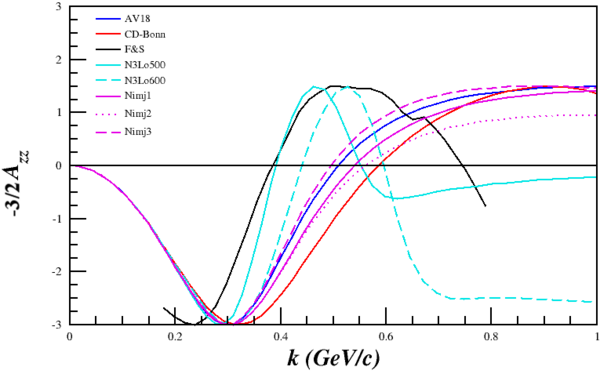
[[Image:2014-05-15-azz-180deg.png|600px]] | [[Image:2014-05-15-azz-180deg.png|600px]] | ||
Revision as of 12:49, 15 May 2014
Recreating F&S Azz
Using the Frankfurt and Strikman equation 7.3,
<math>A_{zz} = R(p_s) = \frac{3(k_t^2/2-k_z^2)}{k^2}\frac{u(k)w(k)\sqrt{2}+\frac{1}{2}w^2(k)}{u^2(k)+w^2(k)}</math>
I'm trying to recreated their Figure 7.5. I don't entirely understand what <math>k_t</math>, <math>k_z</math>, and <math>k</math> are, but if the ratio out front comes out to -3, I can recreate the D(e,e'p) at 180 degrees plot:
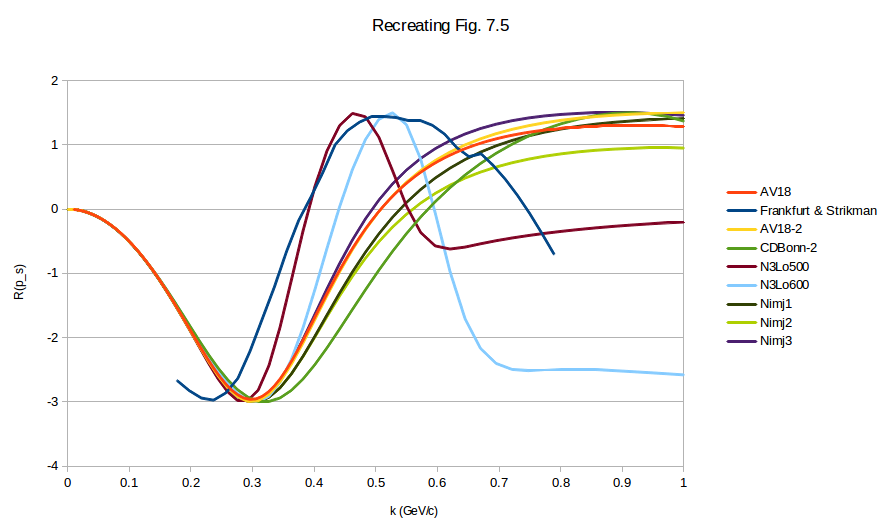
Repeating this same process for all of the wavefunctions that I received from Donal, making sure that the low-k part of the D-state wavefunction is positive as is their convention in Figure 7.1, we see
1981 Report
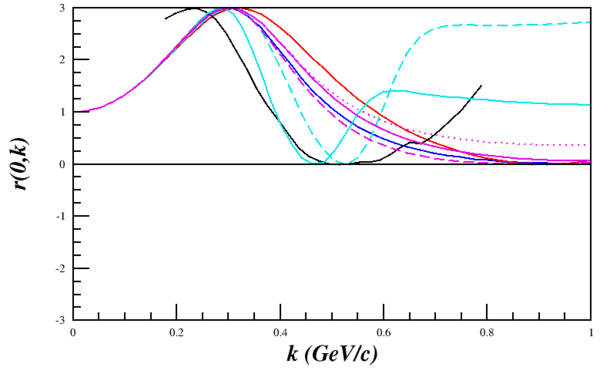
In Frankfurt and Strikman's 1981 report, they go into a bit more detail of how to make the cross section ratios. In particular, on page 258 there is an equation (3.19 and 3.20) for the ratio of cross sections with respect to k,
<math>r(\xi,k)=1+\left(\frac{3(k\xi)^2}{k^2}-1\right)\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>
where <math>\xi</math> is the D-polarization in the D-rest frame, with <math>\xi=(1,\pm i, 0)/\sqrt{2}</math> for <math>\lambda_D=\pm 1</math>, and <math>\xi=(0,0, 1)</math> for <math>\lambda_D=0</math>. Assuming that <math>k\xi=\vec{k}\cdot\xi</math>, this leads to three possible ratios:
<math>r(\pm 1,k)=1+\left(\frac{3k_1^2-3k_2^2}{2\vec{k}\cdot\vec{k}}-1\right)\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>
<math>r(0,k)=1+\left(\frac{3k_3^2}{\vec{k}\cdot\vec{k}}-1\right)\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>.
If I am understanding their kinematic variables correctly, then the virtual-photon points along the <math>\hat{z}</math> axis, so in the case of a nucleon being knocked-out at 180deg, <math>k_1=0, k2=0, k_3=|\vec{k}|</math>. This leads to, in the case of <math>r(0,k)</math> for their Fig. 3.9a,
<math>r(0,k)=1+2\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>,
which can be recreated using the current wavefunctions.
This would make their Fig. 7.5 from their 1988 report simply <math>A_{zz} = r(\pm 1,k)-r(0,k)</math> for D(e,e'p) with p at 180deg, which can also be reproduced.