Difference between revisions of "Elong-14-04-16"
| Line 38: | Line 38: | ||
[[Image:2014-08-21-Pzz-vs-m0.png]] | [[Image:2014-08-21-Pzz-vs-m0.png]] | ||
| + | |||
| + | Or, in terms of an overly-simplistic animation, | ||
| + | |||
| + | [[Image:2014-08-22-Pzz-animation-food.gif]] | ||
=Deuteron Shape= | =Deuteron Shape= | ||
Revision as of 10:13, 22 August 2014
Deuteron Polarization
Being a spin-1 particle, the deuteron has three spin sub-states that can be filled: <math>m_J=+1,~m_J=0,~m_J=-1</math>. For a given quantity of deuterons, the polarization is measured based on the population <math>p_m</math> in each substate. The population is defined as
<math>p_m=\frac{N_m}{N_1+N_0+N_{-1}}</math>
where <math>N_m</math> is the number of deuterons in a given substate. In a system of pure deuterons, the normalization of the populations is
<math>p_1+p_0+p_{-1}=1</math>.
Vector polarization depends only on the <math>m_J=\pm 1</math> populations, such that
<math>P_z = p_1 - p_{-1}~</math>.
It has a range of <math>-1<P_z<1~</math>.
If the <math>m_1</math> state is filled, then <math>p_1=1,~p_{-1}=0,~p_0=0</math> and <math>P_z=1~</math>.
If the <math>m_{-1}</math> state is filled, then <math>p_1=0,~p_{-1}=1,~p_0=0</math> and <math>P_z=-1~</math>.
If the <math>m_0</math> state is filled, then <math>p_1=0,~p_{-1}=0,~p_0=1</math> and <math>P_z=0~</math>.
Tensor polarization depends on the combined <math>m_J=\pm 1</math> populations, as well as the <math>m_J=0</math> population such that
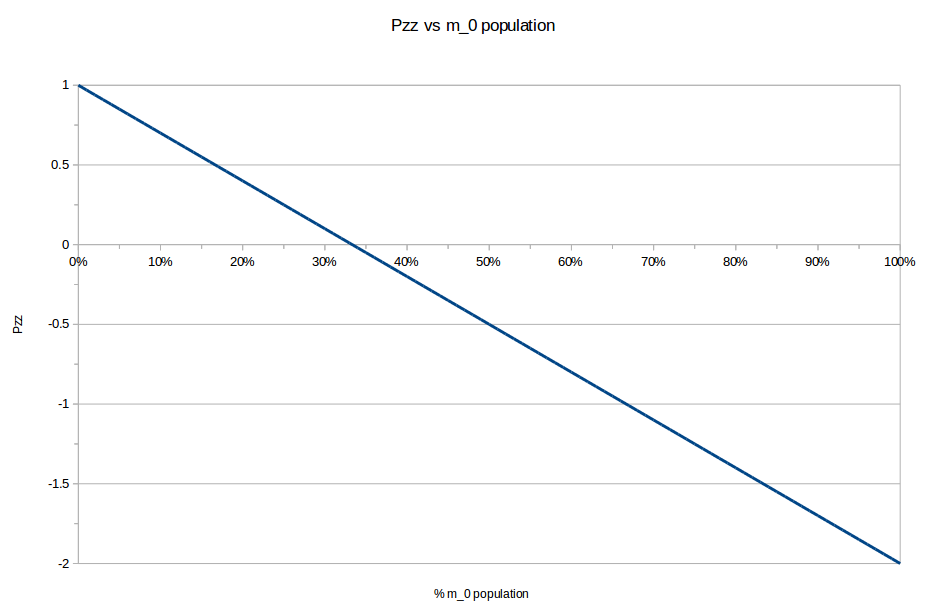
<math>P_{zz} = (p_1 + p_{-1}) - 2p_0~</math>.
It has a range of <math>-2<P_{zz}<1~</math>.
If the <math>m_1</math> and <math>m_{-1}</math> states are filled, then <math>(p_1 + p_{-1})=1,~p_0=0</math> and <math>P_{zz}=1~</math>.
If the combined <math>m_1</math> and <math>m_{-1}</math> states equal the <math>m_0</math> state, then <math>(p_1+p_{-1})=0.5,~p_0=0.5</math> and <math>P_{zz}=-0.5~</math>
If the <math>m_0</math> state is filled, then <math>(p_1 + p_{-1})=0,~p_0=1</math> and <math>P_{zz}=-2~</math>.
Or, in terms of an overly-simplistic animation,
Deuteron Shape
From the video made by S.C. Pieper, et al., I extracted the tensor and vector polarization frames and made repeating videos of each. When we vector-polarize or tensor-polarize, the probability densities for the deuteron look like:
| m_s=±1 | m_s=0 |
|---|---|
 |
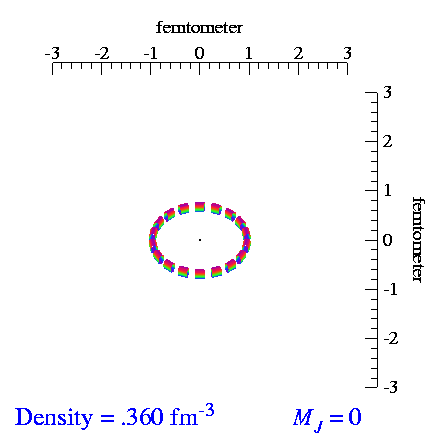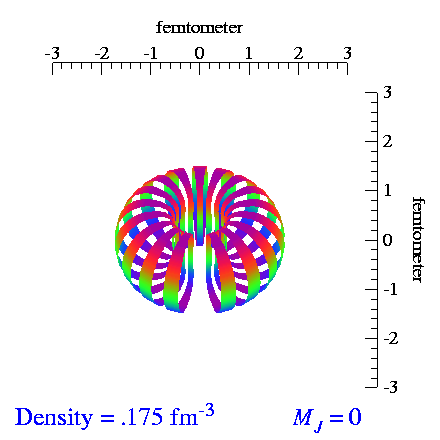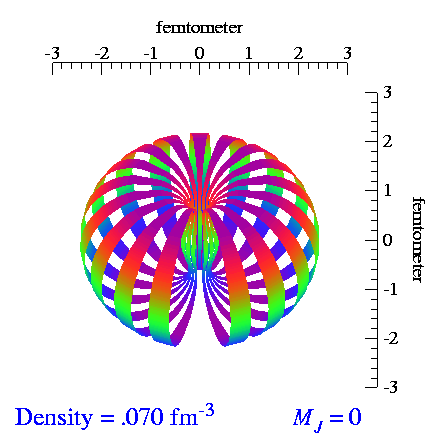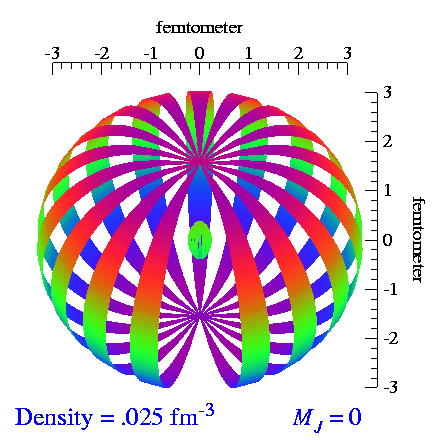
|
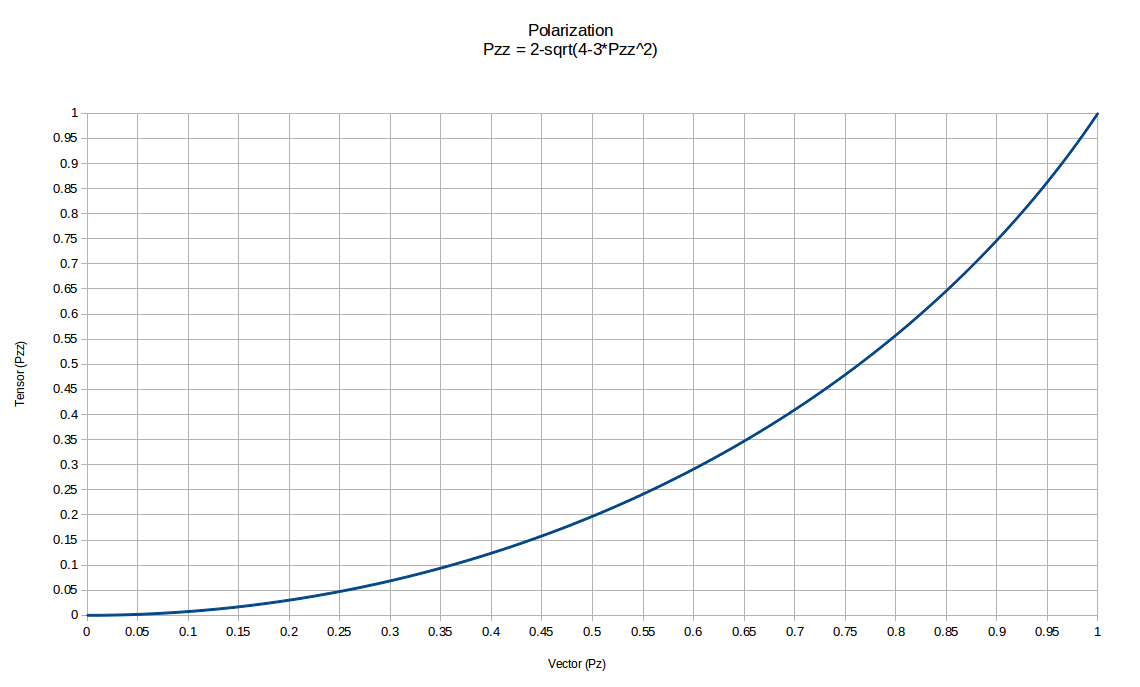
Tensor Polarization Relation to Vector Polarization
Tensor polarization is related to the vector polarization by <math>P_z=2-\sqrt{4-3P_{zz}^2}</math>
Deuteron States
From basic quantum mechanics, we know that the possible states for 2 nucleons are
the isospin singlet with S=0:
- <math>|\uparrow \downarrow> - |\downarrow \uparrow></math> with <math>m_s=0</math>, <math>L=1</math>
and the isospin triplet with S=1:
- <math>|\uparrow \uparrow></math> with <math>m_s=+1</math>, <math>L=0</math>
- <math>|\uparrow \downarrow> + |\downarrow \uparrow></math> with <math>m_s=0</math>, <math>L=1</math>
- <math>|\downarrow \downarrow></math> with <math>m_s=-1</math>, <math>L=2</math>
For the deuteron, <math>J=1</math> and <math>P=+1</math>. This kills both of the <math>m_s=0</math> states, since they cannot simultaneously have <math>J=1</math> and <math>P=+1</math> since <math>P=(-1)^L</math>.
This leaves only two possible states:
- <math>|\uparrow \uparrow></math> with <math>m_s=+1</math>, <math>L=0</math>
- <math>|\downarrow \downarrow></math> with <math>m_s=-1</math>, <math>L=2</math>
Angular Momentum Analysis
Now, let's look at each of these a bit more indepth according to their angular momentum components
| J | <math>m_J</math> | L | <math>m_L</math> | S | <math>m_S</math> | <math>\pi = -1^L</math> | T | <math>^{2S+1}L_J</math> |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 | 0 | + | 1 | <math>^1 S_0</math> |
| 1 | ±1 | 0 | 0 | 1 | ±1 | + | 0 | <math>^3 S_1</math> |
| 1 | 1 | 2 | 1 | 1 | 0 | - | 0 | <math>^1 P_1</math> |
| 1 | 0 | 2 | -1 | 1 | 1 | - | 1 | <math>^3 P_0</math> |
| 1 | 0 | 2 | 1 | 1 | -1 | - | 1 | <math>^3 P_0</math> |
| 1 | 1 | 2 | 1 | 1 | 0 | - | 1 | <math>^3 P_1</math> |
| 1 | 2 | 2 | 1 | 1 | 1 | - | 1 | <math>^3 P_2</math> |
| 1 | 2 | 2 | 2 | 1 | 0 | + | 1 | <math>^1 D_2</math> |
| 1 | 1 | 2 | 2 | 1 | -1 | + | 0 | <math>^3 D_1</math> |
| 1 | -1 | 2 | -2 | 1 | +1 | + | 0 | <math>^3 D_1</math> |
| 3 | 3 | 2 | 2 | 1 | 1 | + | 0 | <math>^3 D_2</math> |
| 3 | 3 | 2 | 2 | 1 | 1 | + | 0 | <math>^3 D_3</math> |
When we remove all of the states that can't exist, we're left with two mentioned in the last section:
| J | <math>m_J</math> | L | <math>m_L</math> | S | <math>m_S</math> | <math>\pi = -1^L</math> | T | <math>^{2S+1}L_J</math> |
|---|---|---|---|---|---|---|---|---|
| 1 | ±1 | 0 | 0 | 1 | ±1 | + | 0 | <math>^3 S_1</math> |
| 1 | 1 | 2 | 2 | 1 | -1 | + | 0 | <math>^3 D_1</math> |
| 1 | -1 | 2 | -2 | 1 | +1 | + | 0 | <math>^3 D_1</math> |
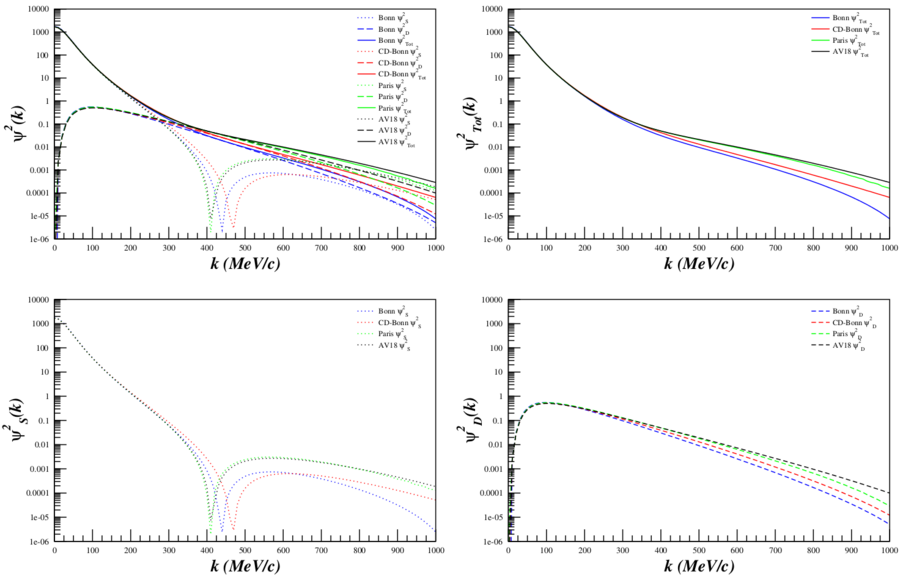
S and D States
A variety of models have looked at the wavefunction from the S- and D-states.
File:2014-04-24-deuteron-wavefunction-s-d-states.pdf
--E. Long 19:53, 24 April 2014 (UTC)