Difference between revisions of "Elong-13-09-18"
From HallCWiki
Jump to navigationJump to search| (3 intermediate revisions by the same user not shown) | |||
| Line 80: | Line 80: | ||
==Fixed uncertainty due to large asymmetry== | ==Fixed uncertainty due to large asymmetry== | ||
| − | Previously, the code was using a simplified | + | Previously, the code was using a simplified $\delta A_{zz} = \frac{4}{f \cdot Pzz \sqrt{N}}$. This gave all of the above uncertainties, as well as this one: |
[[Image:2013-09-19-old-error.png]] | [[Image:2013-09-19-old-error.png]] | ||
| − | Going back through [http://nuclear.unh.edu/~elong/analysis_files/2013-05-16/Azz_error.pdf the uncertainty tech note], the assumption of a small asymmetry isn't made until after Eq. 28. Utilizing the full uncertainty (Eq. 28 and 25), | + | Going back through [http://nuclear.unh.edu/~elong/analysis_files/2013-05-16/Azz_error.pdf the uncertainty tech note], the assumption of a small asymmetry isn't made until after Eq. 28. Utilizing the full uncertainty (Eq. 28 and 25), $\delta A_{zz} = \frac{2}{f \cdot Pzz}\sqrt{\frac{N_{Pol}}{N_u^2}+\frac{N_{Pol}^2}{N_u^3}}$, the uncertainties change (very slightly) to: |
[[Image:2013-09-19-new-error.png]] | [[Image:2013-09-19-new-error.png]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Latest revision as of 13:53, 18 October 2023
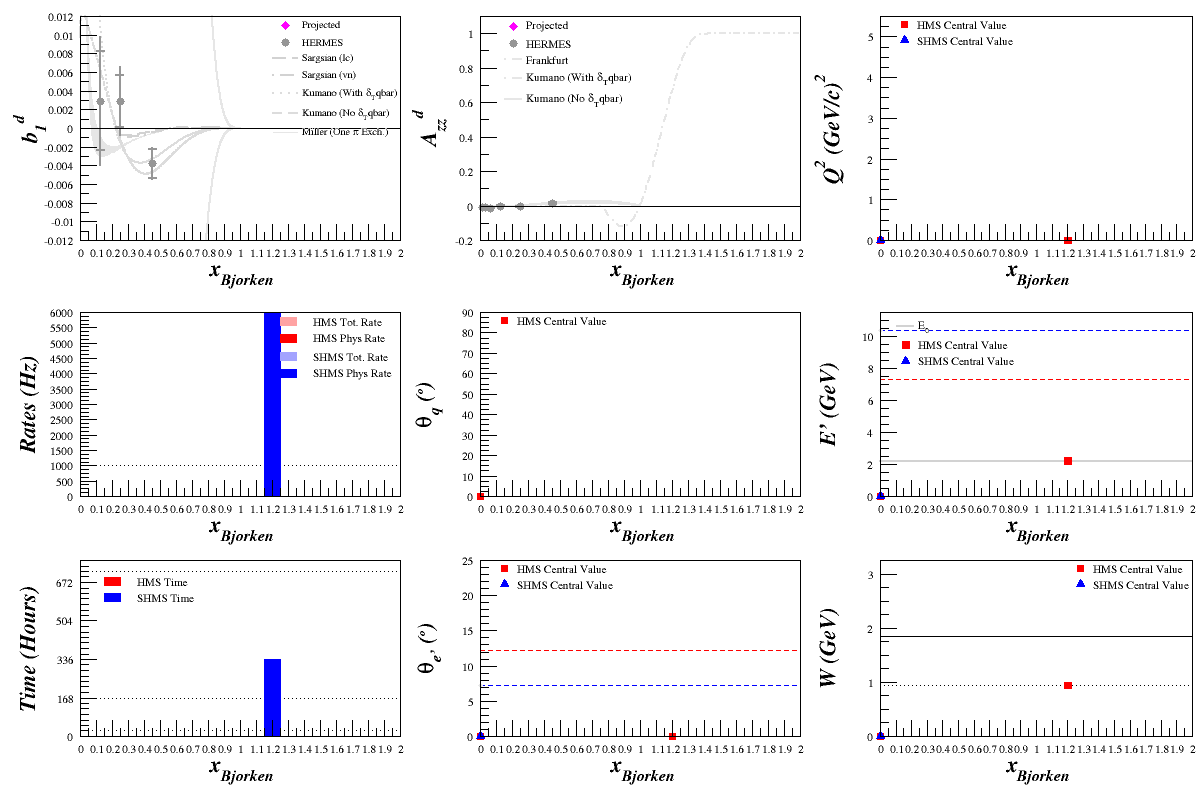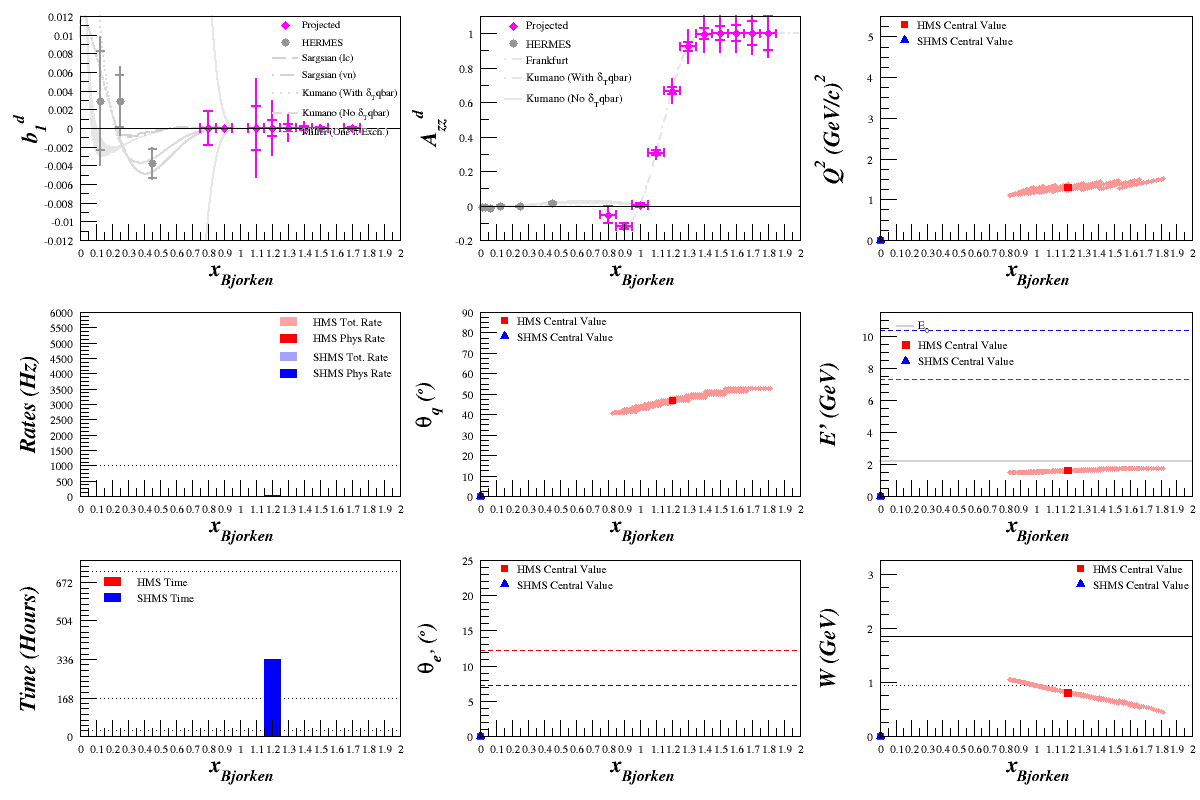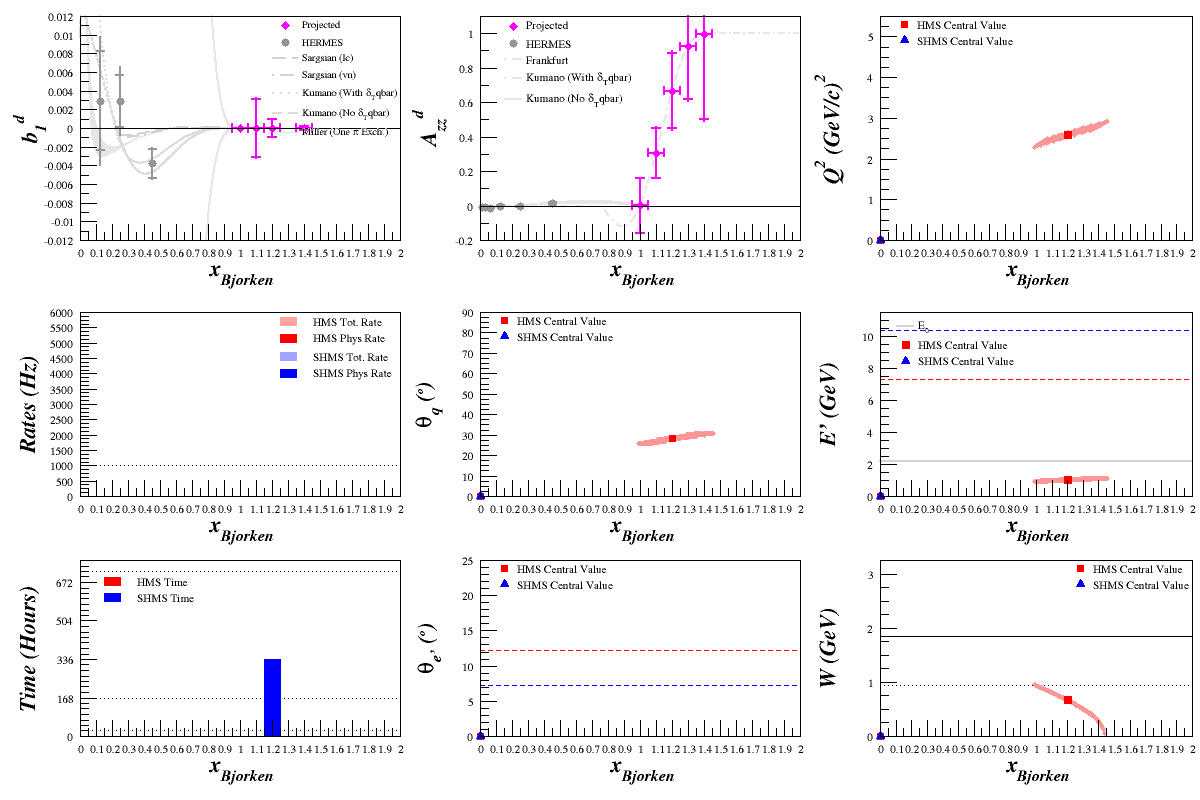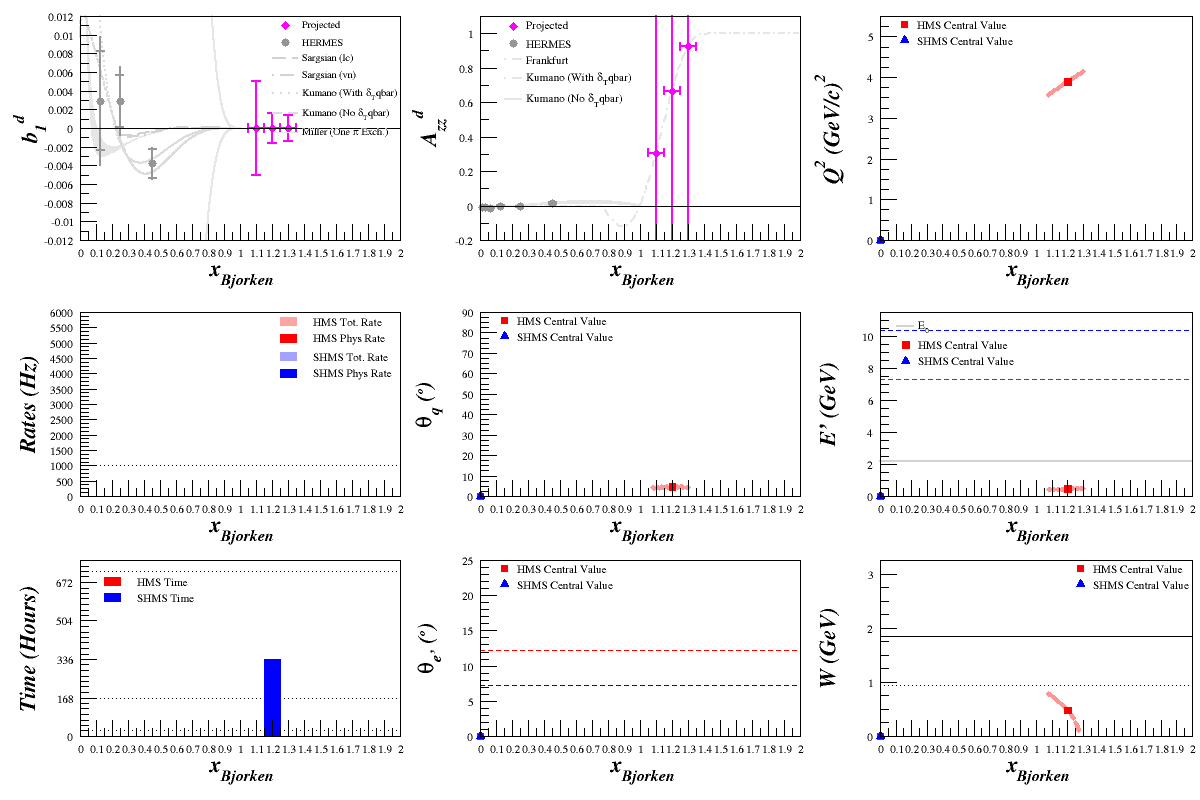
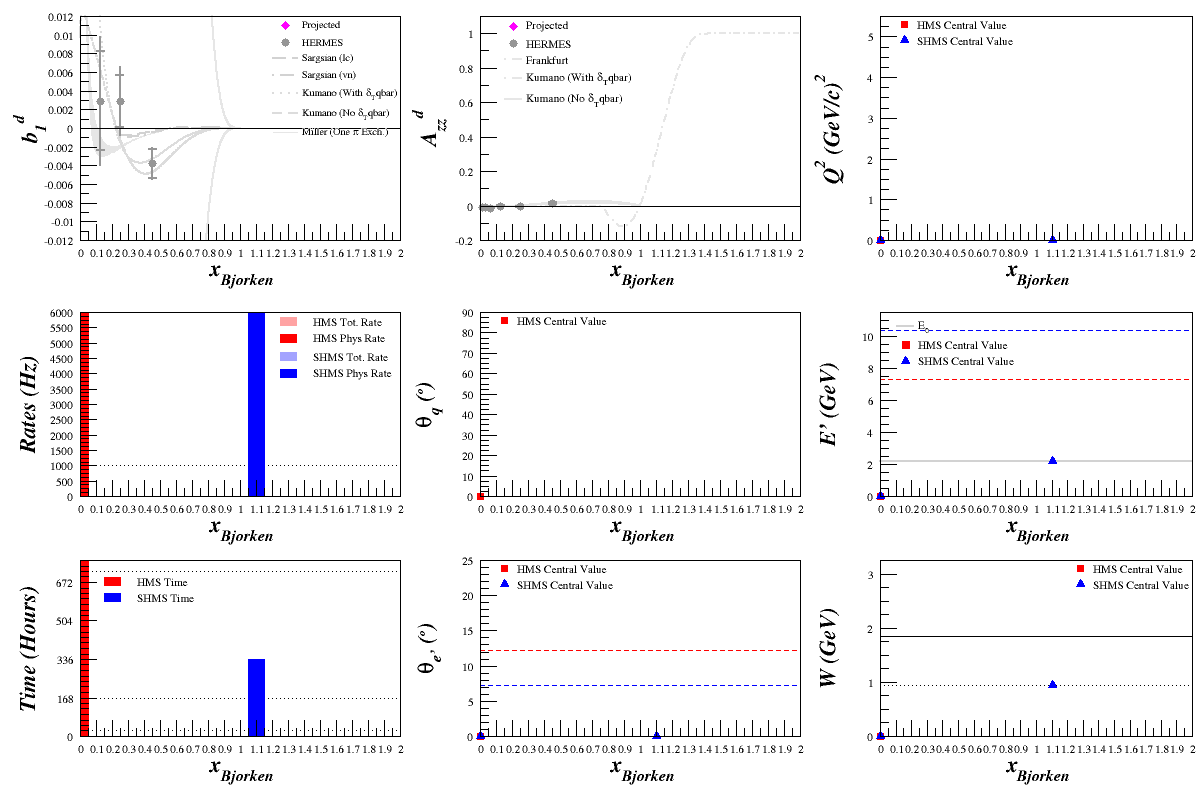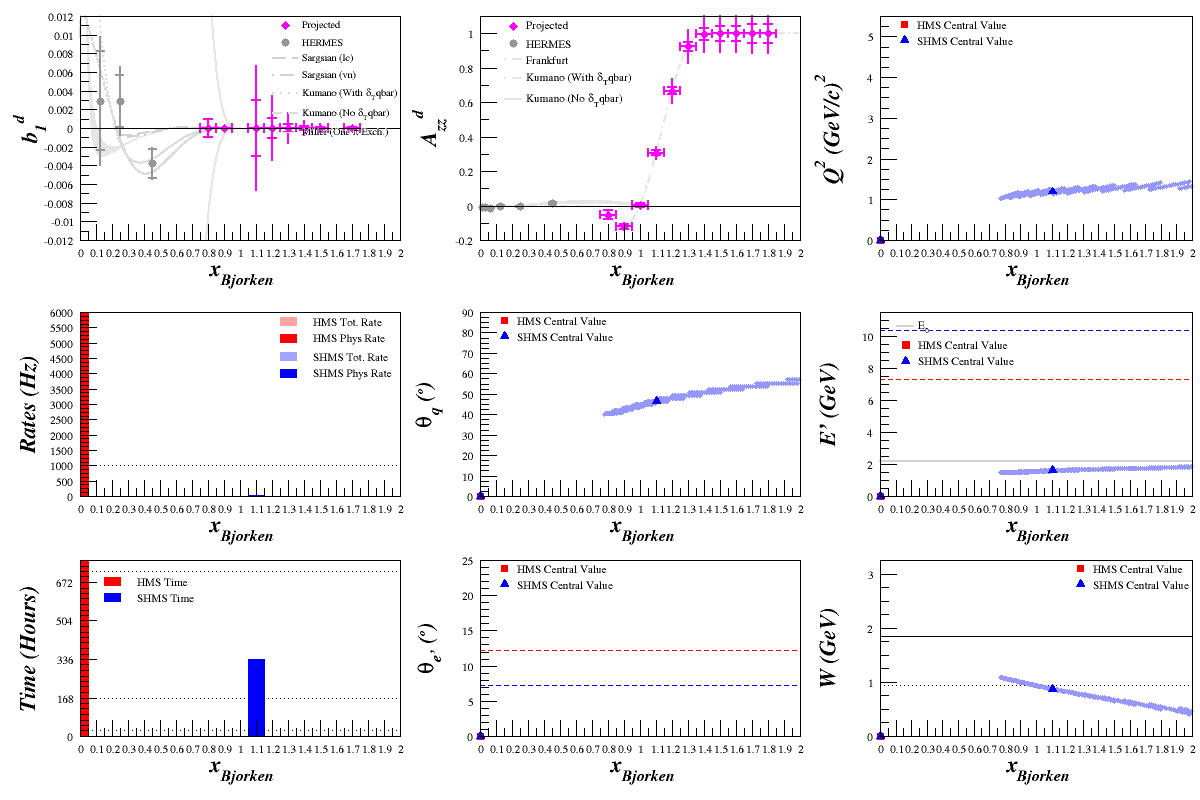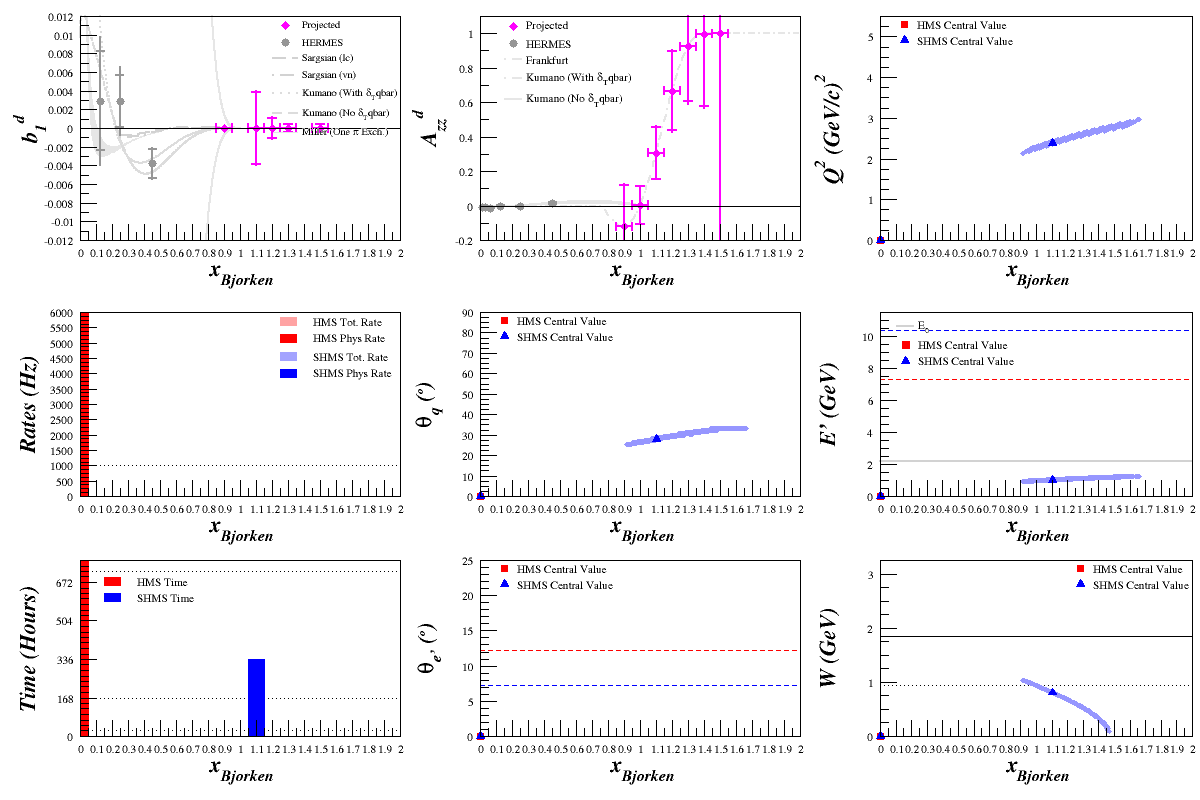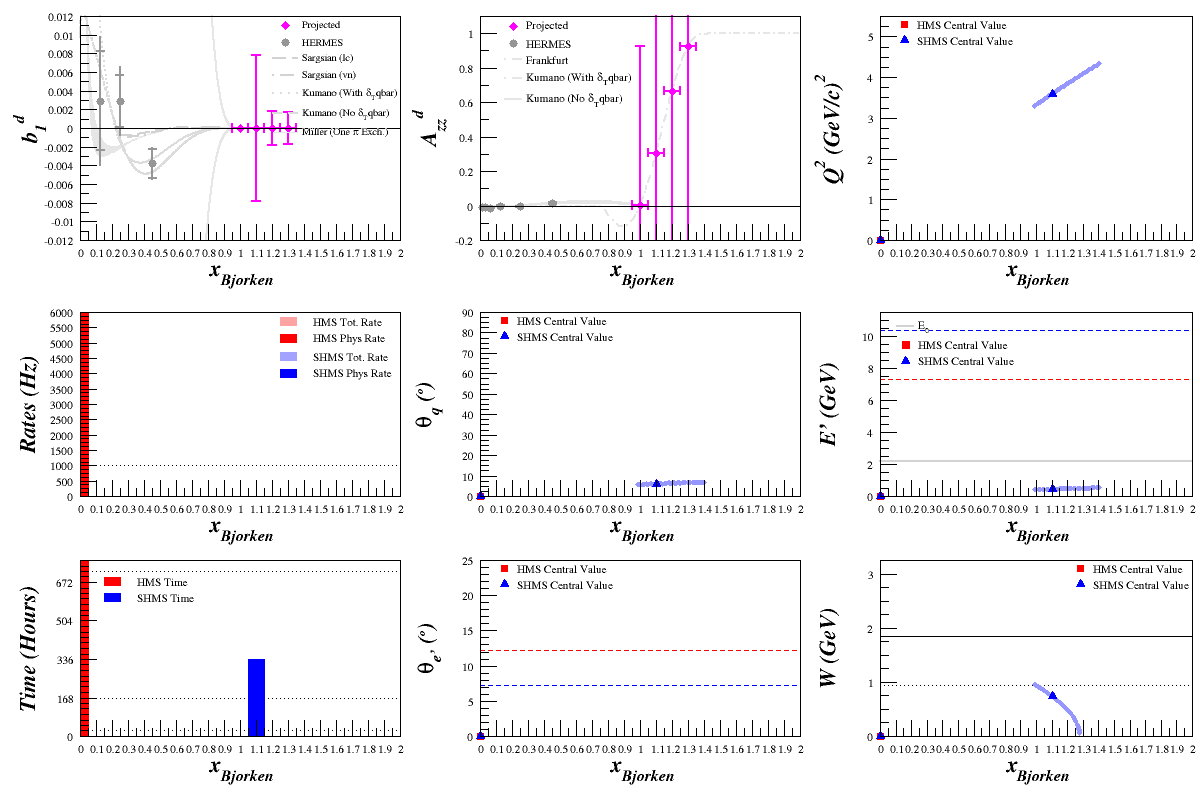
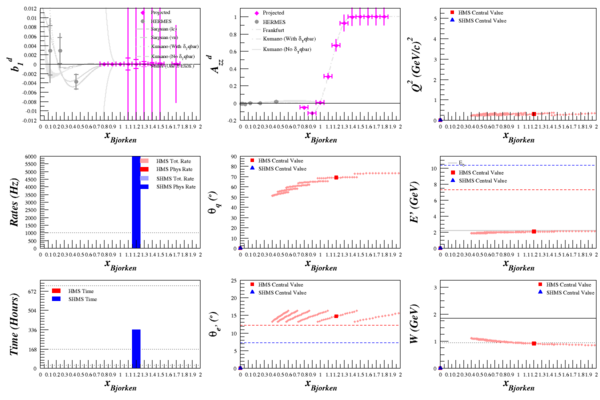
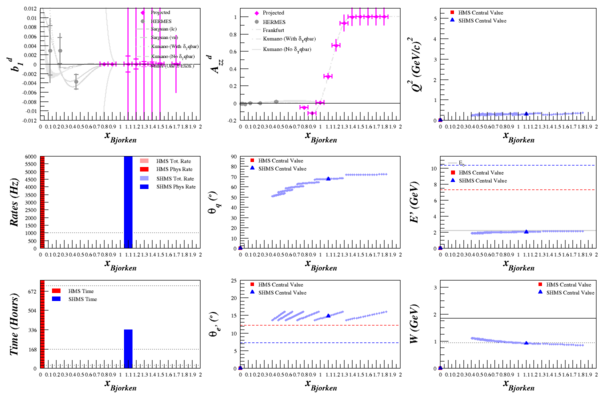
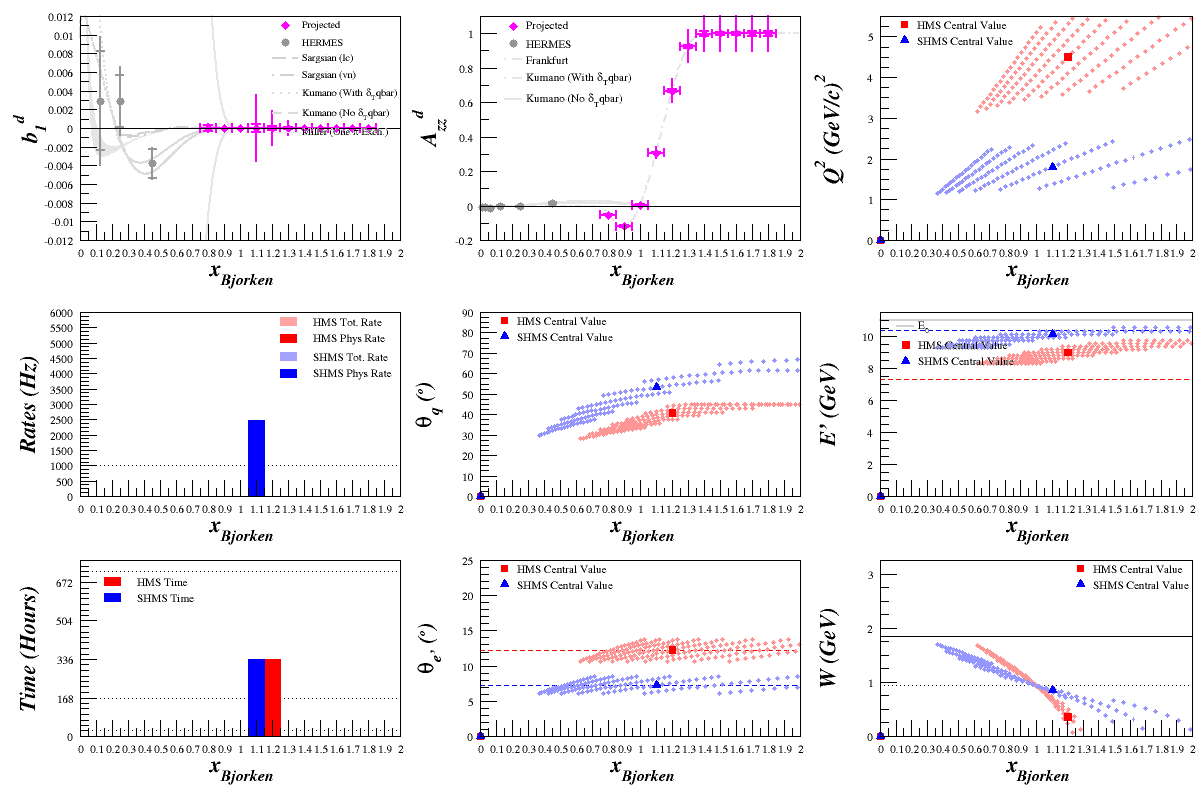
Optimizing Azz in QE and x>1 Range
Beam Energy = 2.2 GeV
HMS
SHMS
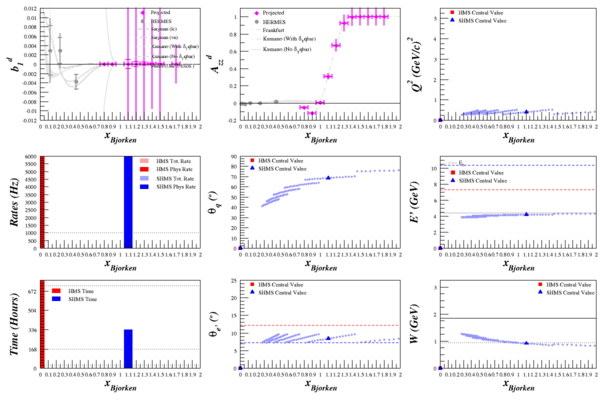
Beam Energy = 4.4 GeV
HMS
SHMS
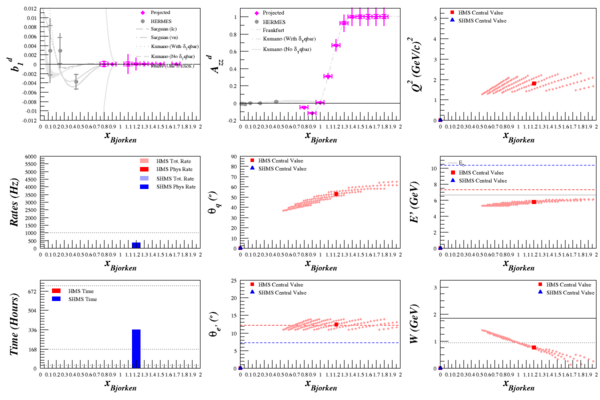
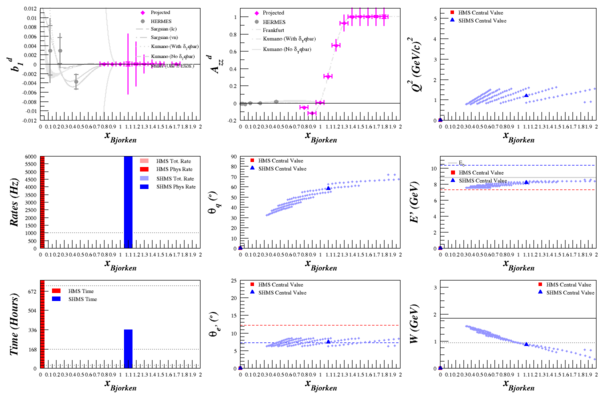
Beam Energy = 6.6 GeV
HMS
SHMS
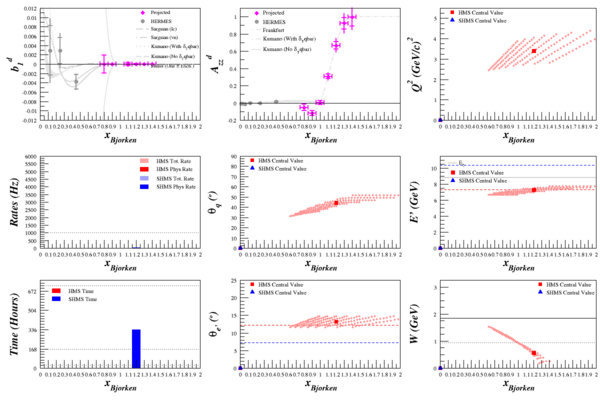
Beam Energy = 8.8 GeV
HMS
SHMS
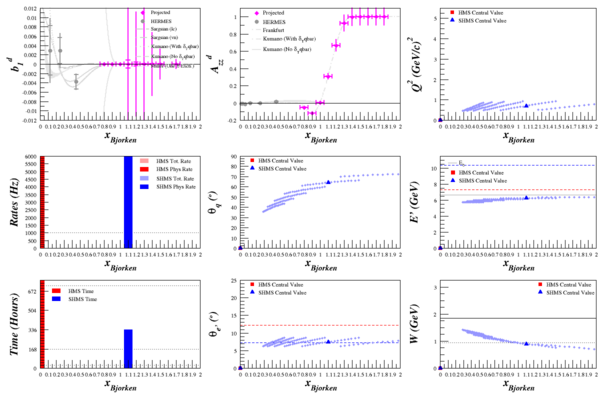
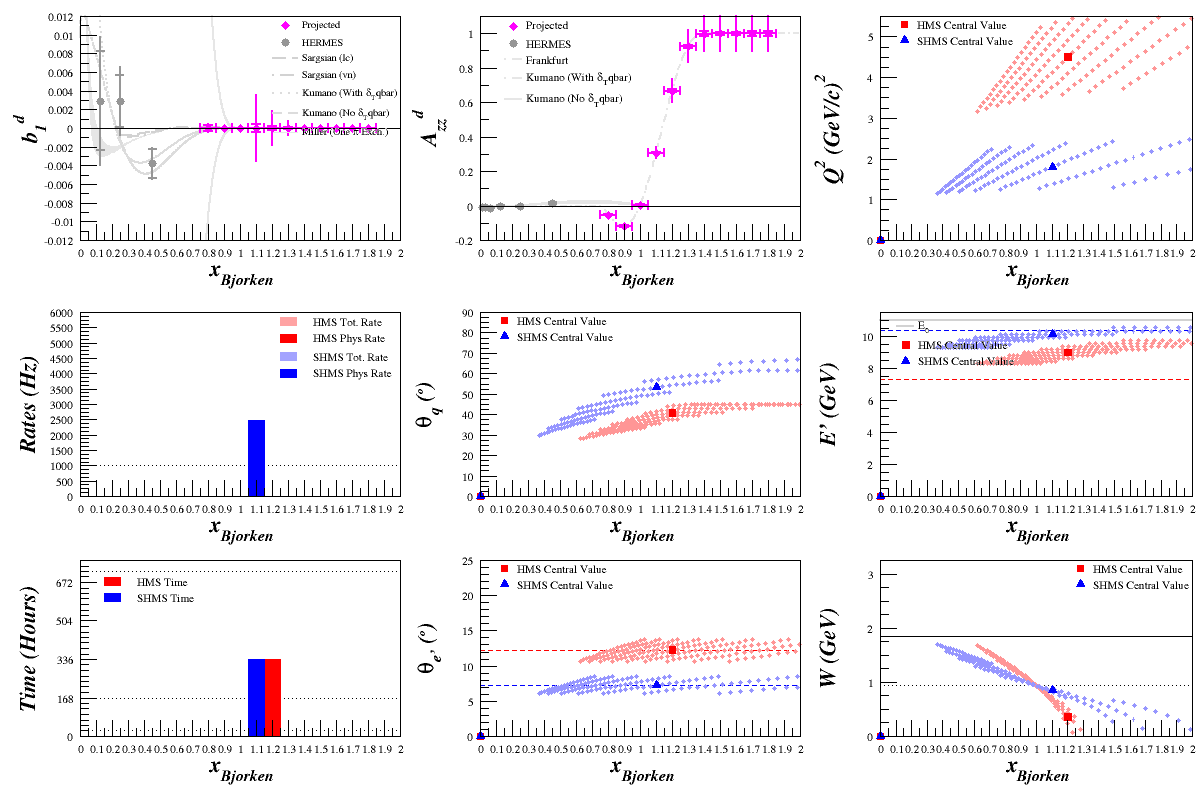
Beam Energy = 11.0 GeV
HMS
SHMS
Optimization Results
Beam Energy = 2.2 GeV
Beam Energy = 4.4 GeV
Beam Energy = 6.6 GeV
Beam Energy = 8.8 GeV
Beam Energy = 11.0 GeV
(None for HMS -- rates drop off dramatically by the time it's in a good kinematics range)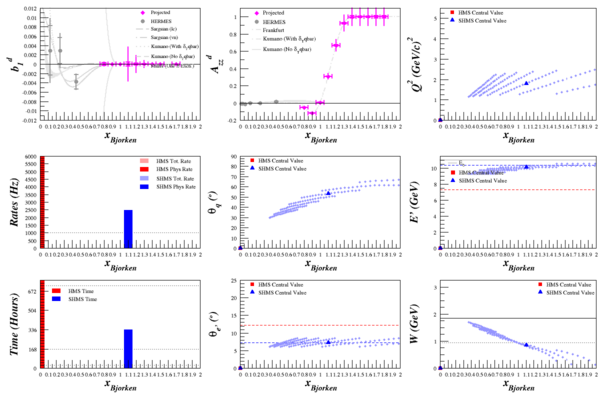
Fixed uncertainty due to large asymmetry
Previously, the code was using a simplified $\delta A_{zz} = \frac{4}{f \cdot Pzz \sqrt{N}}$. This gave all of the above uncertainties, as well as this one:
Going back through the uncertainty tech note, the assumption of a small asymmetry isn't made until after Eq. 28. Utilizing the full uncertainty (Eq. 28 and 25), $\delta A_{zz} = \frac{2}{f \cdot Pzz}\sqrt{\frac{N_{Pol}}{N_u^2}+\frac{N_{Pol}^2}{N_u^3}}$, the uncertainties change (very slightly) to: