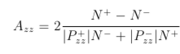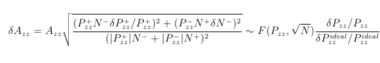Difference between revisions of "Final Look"
| Line 11: | Line 11: | ||
P<sub>zz</sub>=2-(4-3P<sup>2</sup>)<sup>1/2</sup> assuming a Boltzman distribution at thermal equilibrium. <br> | P<sub>zz</sub>=2-(4-3P<sup>2</sup>)<sup>1/2</sup> assuming a Boltzman distribution at thermal equilibrium. <br> | ||
| − | But not at thermal equilibrium under experiment ( | + | But not at thermal equilibrium under experiment (trying not to under estimate error)<br> |
Analytic relation not applicable for tensor Optimization (hole burning)<br> | Analytic relation not applicable for tensor Optimization (hole burning)<br> | ||
| Line 26: | Line 26: | ||
[[Image:sys_error.png|800px]] | [[Image:sys_error.png|800px]] | ||
| + | |||
| + | What about other observables? | ||
| + | |||
| + | Still lots of experimental possibilites with tensor polarization: <br> | ||
| + | 1.) Cross section or Asymmetry (A<sub>xx</sub>) based on Vector Optimized only <br> | ||
| + | 2.) Electrodisintegration <br> | ||
| + | 3.) Photodisintegration <br> | ||
| + | 4.) CLAS photoproduction <br> | ||
Revision as of 10:15, 16 April 2013
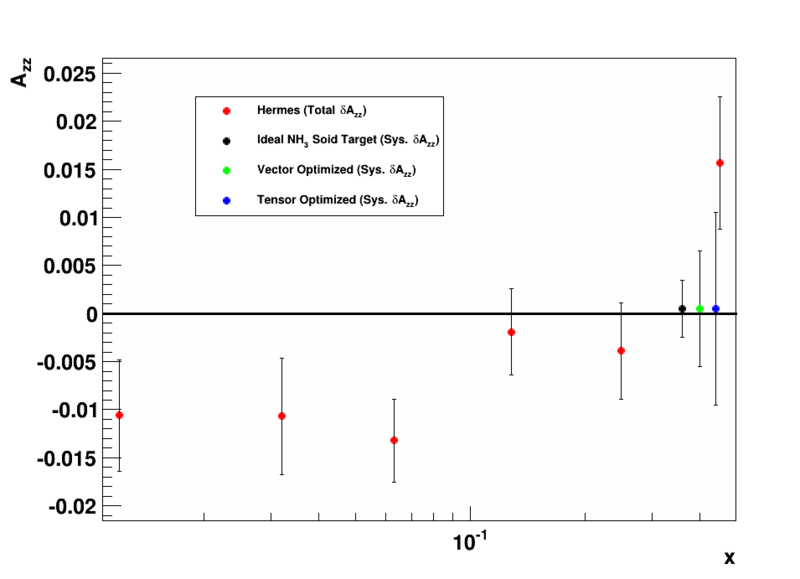
Error estimate based on previous analysis using standard solid polarized targets results indicated in first write-up
based on an asymmetry Azz
with an absolute systematic uncertainty estimated from,
To obtain tensor polarization by optimizing vector polarization we expect a tensor polarization of
Pzz=2-(4-3P2)1/2 assuming a Boltzman distribution at thermal equilibrium.
But not at thermal equilibrium under experiment (trying not to under estimate error)
Analytic relation not applicable for tensor Optimization (hole burning)
Gerneral limitations for all tensor polarized experiments to keep in mind:
1.) Ideal Pzz =2.5%-5%
2.) Vector Optimized Pzz =6.5%-12%
3.) Tensor Optimized Pzz =15%-25%
4.) Negative tensor polarization not yet achieved without hole burning (very unstable)
→ Best Estimates for Cumulative Absolute Uncertainty
What about other observables?
Still lots of experimental possibilites with tensor polarization:
1.) Cross section or Asymmetry (Axx) based on Vector Optimized only
2.) Electrodisintegration
3.) Photodisintegration
4.) CLAS photoproduction