Difference between revisions of "Elong-13-10-01"
(New page: ==Cross Section Calculation== For previous calculations, I was using a simplified version of the cross-section where it was assumed that <math>F_2=2x\cdot F_1</math>, such that <math>\fr...) |
|||
| Line 28: | Line 28: | ||
[[Image:2013-09-30-cs-fixed-fdil.png]] | [[Image:2013-09-30-cs-fixed-fdil.png]] | ||
| + | ==Cross Section Check for b1== | ||
| + | |||
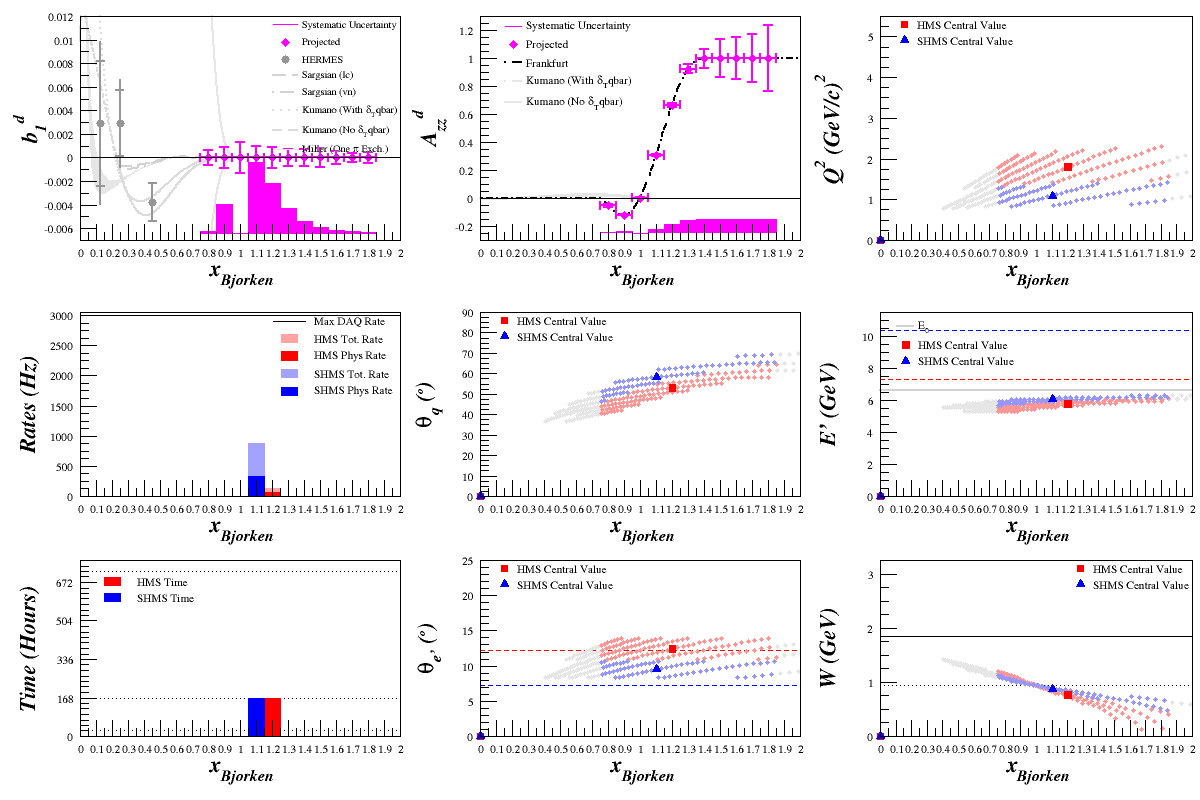
| + | To see if this could cause a problem for the b1 statistics, I did a study of the effects of changing the cross section calculation from the simplified to the full for the b1 kinematics. | ||
| + | |||
| + | {| class="wikitable" style="text-align:center; border-collapse:collapse;" border="1" | ||
| + | ! HMS<br><math>\theta_{e'}=12.50^{\circ}</math><br><math>E'=7.31\mathrm{~GeV}</math> !! SHMS 1<br><math>\theta_{e'}=7.35^{\circ}</math><br><math>E'=6.80\mathrm{~GeV}</math> !! SHMS 2<br><math>\theta_{e'}=8.96^{\circ}</math><br><math>E'=7.45\mathrm{~GeV}</math> !! SHMS 3<br><math>\theta_{e'}=9.85^{\circ}</math> <br><math>E'=7.96\mathrm{~GeV}</math> | ||
| + | |- | ||
| + | | [[Image:2013-10-01-b1-hms-cs.png]] || [[Image:2013-10-01-b1-shms-1-cs.png]] || [[Image:2013-10-01-b1-shms-2-cs.png]] || [[Image:2013-10-01-b1-shms-3-cs.png]] | ||
| + | |- | ||
| + | |} | ||
--[[User:Ellie|E. Long]] 21:20, 1 October 2013 (UTC) | --[[User:Ellie|E. Long]] 21:20, 1 October 2013 (UTC) | ||
Revision as of 16:30, 1 October 2013
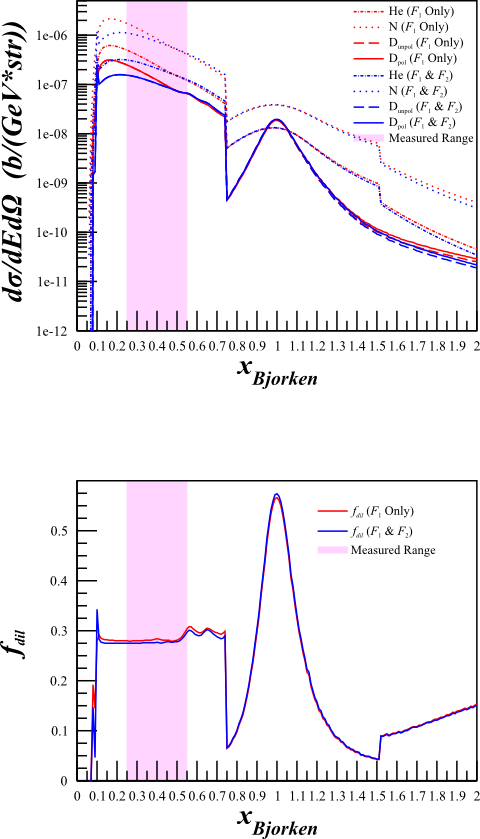
Cross Section Calculation
For previous calculations, I was using a simplified version of the cross-section where it was assumed that <math>F_2=2x\cdot F_1</math>, such that
<math>\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\right]\cdot \left[\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{Q^2 }{2\nu^2} \right] </math>.
Since we're in a region that isn't DIS, I thought that the difference may be important so I incorporated <math>F_2</math> from Bosted and removed the assumption:
<math>\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]</math>.
This increased the statistical uncertainty, particularly in the high-x region. It also lowered the rates dramatically, which gives us some room to play around with a lower <math>Q^2</math>.
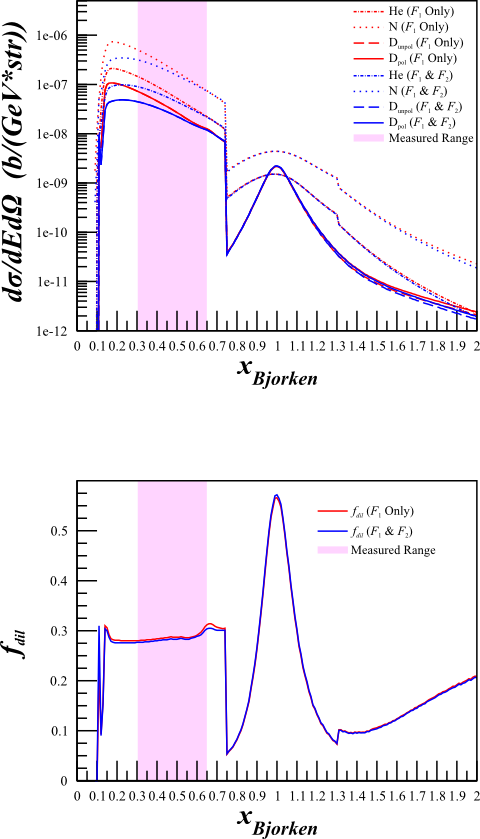
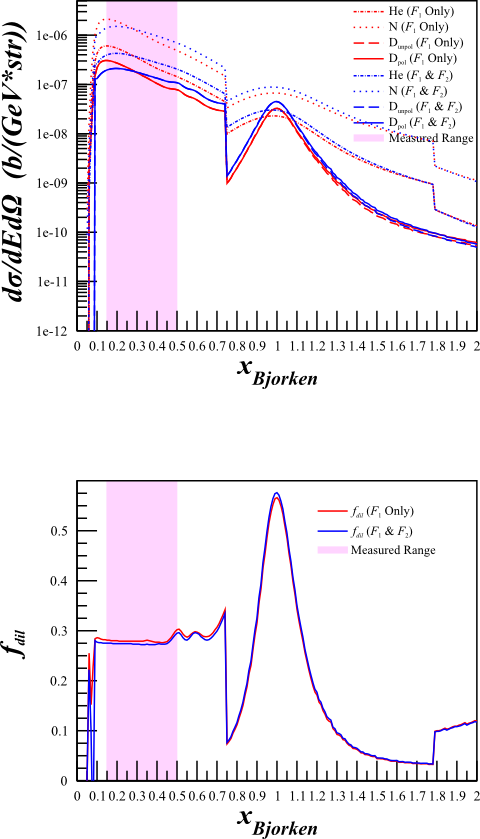
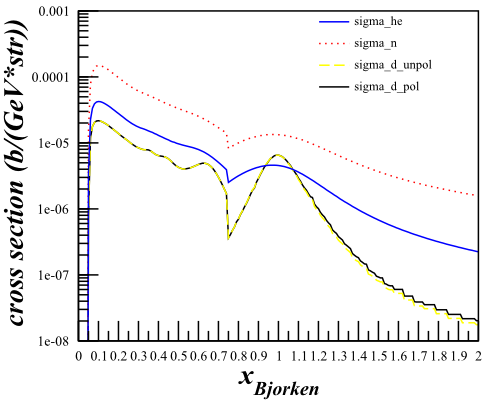
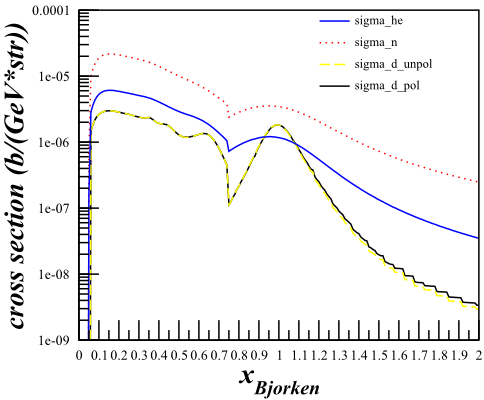
Although this changes the cross sections quite a bit,
| <math>F_1 \mathrm{~Only}</math> | <math>F_1\mathrm{~and~}F_2</math> |
|---|---|
 |
|
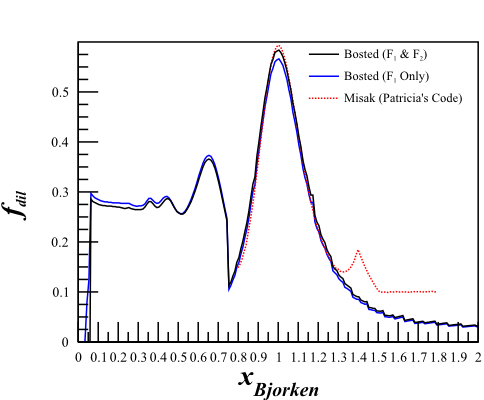
The dilution factor is nearly identical.
Cross Section Check for b1
To see if this could cause a problem for the b1 statistics, I did a study of the effects of changing the cross section calculation from the simplified to the full for the b1 kinematics.
--E. Long 21:20, 1 October 2013 (UTC)