Difference between revisions of "Elong-14-04-16"
| Line 44: | Line 44: | ||
Now, let's look at each of these a bit more indepth according to their angular momentum components | Now, let's look at each of these a bit more indepth according to their angular momentum components | ||
| − | {|border="1px" align="center" cellpadding="10" cellspacing="0" | + | {|class="wikitable" border="1px" align="center" cellpadding="10" cellspacing="0" style="text-align:center;" |
! State !! <math>J</math> !! <math>m_j</math> !! <math>L</math> !! <math>m_l</math> !! <math>S</math> !! <math>m_s</math> | ! State !! <math>J</math> !! <math>m_j</math> !! <math>L</math> !! <math>m_l</math> !! <math>S</math> !! <math>m_s</math> | ||
| + | |- | ||
| + | | <math>|\uparrow \uparrow></math> (S-wave, 96%) || 1 || +1<br>0<br>-1 || 0 || 0<br>0<br>0 || 1 || +1<br>0<br>-1 | ||
|- | |- | ||
| − | | <math>|\ | + | | <math>|\downarrow \downarrow></math> (D-wave, 4%) || 1 || +1<br>+1<br>0<br>+1<br>0<br>-1<br>-1<br>0<br>+1 || 2 || +2<br>+1<br>+1<br>0<br>0<br>0<br>-1<br>-1<br>-2 || 1 || -1<br>0<br>-1<br>+1<br>0<br>-1<br>0<br>+1<br>+1 |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
|} | |} | ||
Revision as of 13:37, 18 April 2014
Deuteron Shape
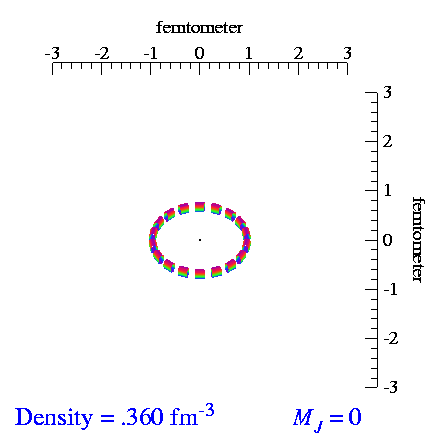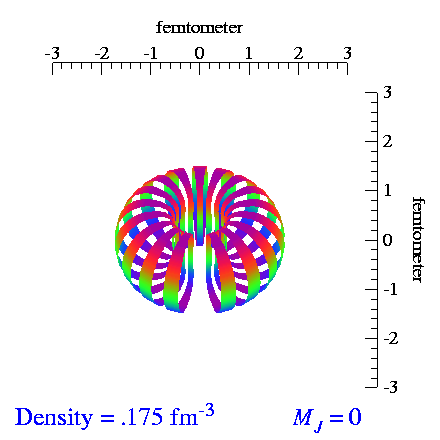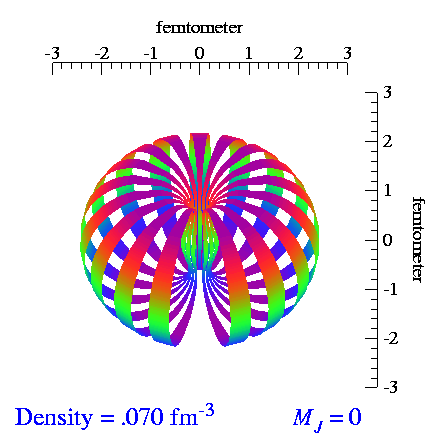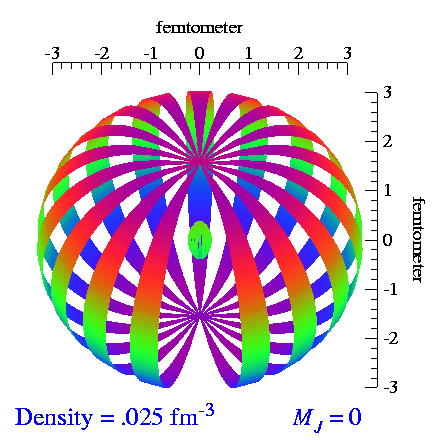
From the video make by S.C. Pieper, et al., I extracted the tensor and vector polarization frames and made repeating videos of each. When we vector-polarize or tensor-polarize, the probability densities for the deuteron look like:
| Vector | Tensor |
|---|---|
 |
|
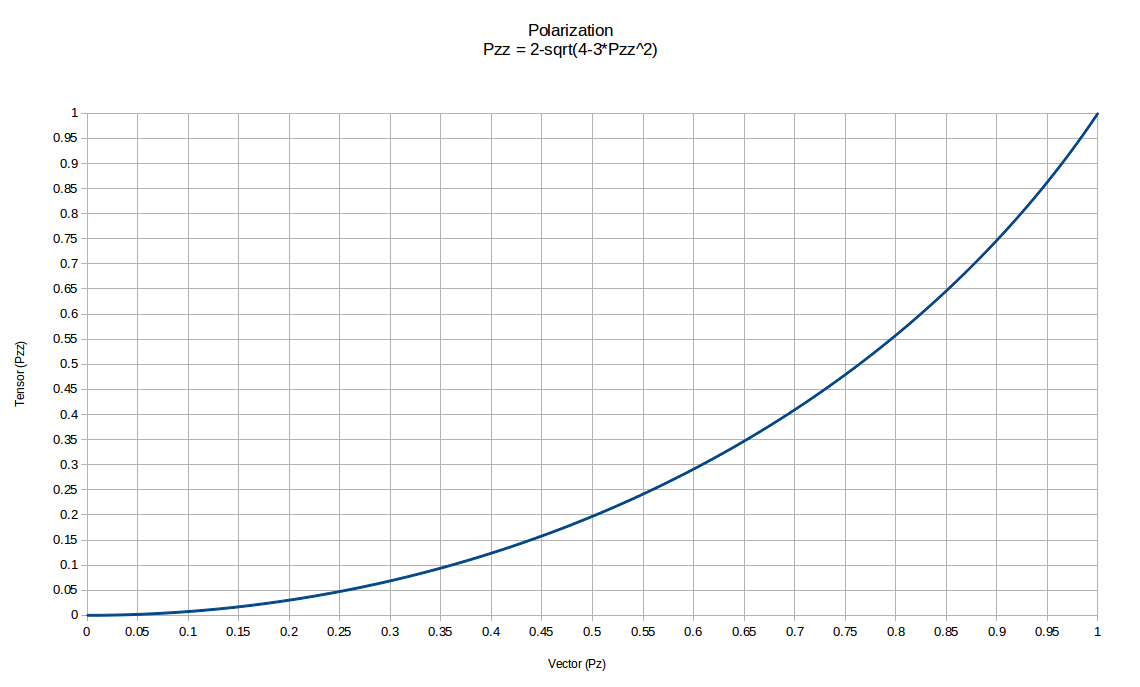
Tensor Polarization Relation to Vector Polarization
Tensor polarization is related to the vector polarization by <math>P_z=2-\sqrt{4-3P_{zz}^2}</math>
Deuteron States
From basic quantum mechanics, we know that the possible states for 2 nucleons are
the isospin singlet with S=0:
- <math>|\uparrow \downarrow> - |\downarrow \uparrow></math> with <math>m_s=0</math>, <math>L=1</math>
and the isospin triplet with S=1:
- <math>|\uparrow \uparrow></math> with <math>m_s=+1</math>, <math>L=0</math>
- <math>|\uparrow \downarrow> + |\downarrow \uparrow></math> with <math>m_s=0</math>, <math>L=1</math>
- <math>|\downarrow \downarrow></math> with <math>m_s=-1</math>, <math>L=2</math>
For the deuteron, <math>J=1</math> and <math>P=+1</math>. This kills both of the <math>m_s=0</math> states, since they cannot simultaneously have <math>J=1</math> and <math>P=+1</math> since <math>P=(-1)^L</math>.
This leaves only two possible states:
- <math>|\uparrow \uparrow></math> with <math>m_s=+1</math>, <math>L=0</math>
- <math>|\downarrow \downarrow></math> with <math>m_s=-1</math>, <math>L=2</math>
Angular Momentum Analysis
Now, let's look at each of these a bit more indepth according to their angular momentum components
| State | <math>J</math> | <math>m_j</math> | <math>L</math> | <math>m_l</math> | <math>S</math> | <math>m_s</math> |
|---|---|---|---|---|---|---|
| \uparrow \uparrow></math> (S-wave, 96%) | 1 | +1 0 -1 |
0 | 0 0 0 |
1 | +1 0 -1 |
| \downarrow \downarrow></math> (D-wave, 4%) | 1 | +1 +1 0 +1 0 -1 -1 0 +1 |
2 | +2 +1 +1 0 0 0 -1 -1 -2 |
1 | -1 0 -1 +1 0 -1 0 +1 +1 |