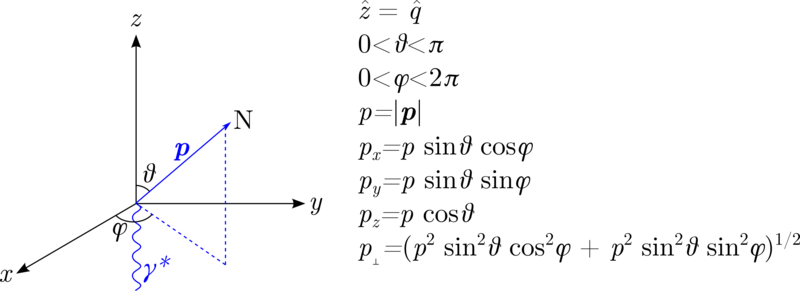Difference between revisions of "Elong-14-05-15b"
| Line 11: | Line 11: | ||
<math>r(0,k)=1+\left(\frac{3k_3^2}{\vec{k}\cdot\vec{k}}-1\right)\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>. | <math>r(0,k)=1+\left(\frac{3k_3^2}{\vec{k}\cdot\vec{k}}-1\right)\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>. | ||
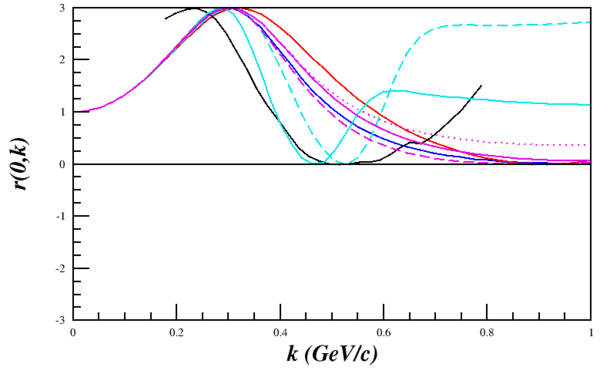
| − | If I am understanding their kinematic variables correctly, then the virtual-photon points along the <math>\hat{z}</math> axis, so in the case of a nucleon being knocked-out at 180deg, <math>k_1=0, | + | If I am understanding their kinematic variables correctly, then the virtual-photon points along the <math>\hat{z}</math> axis, so in the case of a nucleon being knocked-out at 180deg, <math>k_1=0, k_2=0, k_3=|\vec{k}|</math>. This leads to, in the case of <math>r(0,k)</math> for their Fig. 3.9a, |
<math>r(0,k)=1+2\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>, | <math>r(0,k)=1+2\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>, | ||
Revision as of 10:53, 16 May 2014
1981 Report
In Frankfurt and Strikman's 1981 report, they go into a bit more detail of how to make the cross section ratios. In particular, on page 258 there is an equation (3.19 and 3.20) for the ratio of cross sections with respect to k,
<math>r(\xi,k)=1+\left(\frac{3(k\xi)^2}{k^2}-1\right)\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>
where <math>\xi</math> is the D-polarization in the D-rest frame, with <math>\xi=(1,\pm i, 0)/\sqrt{2}</math> for <math>\lambda_D=\pm 1</math>, and <math>\xi=(0,0, 1)</math> for <math>\lambda_D=0</math>. Assuming that <math>k\xi=\vec{k}\cdot\xi</math>, this leads to three possible ratios:
<math>r(\pm 1,k)=1+\left(\frac{3k_1^2-3k_2^2}{2\vec{k}\cdot\vec{k}}-1\right)\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>
<math>r(0,k)=1+\left(\frac{3k_3^2}{\vec{k}\cdot\vec{k}}-1\right)\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>.
If I am understanding their kinematic variables correctly, then the virtual-photon points along the <math>\hat{z}</math> axis, so in the case of a nucleon being knocked-out at 180deg, <math>k_1=0, k_2=0, k_3=|\vec{k}|</math>. This leads to, in the case of <math>r(0,k)</math> for their Fig. 3.9a,
<math>r(0,k)=1+2\frac{u(k)w(k)\sqrt{2}+w^2(k)/2}{u^2(k)+w^2(k)}</math>,
which can be recreated using the current wavefunctions.
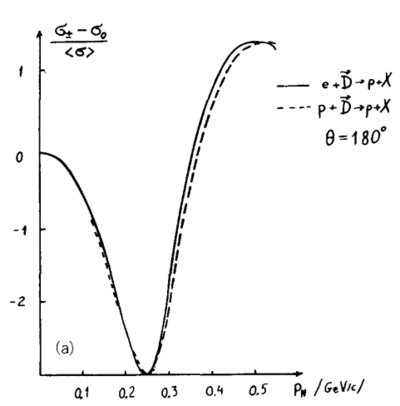
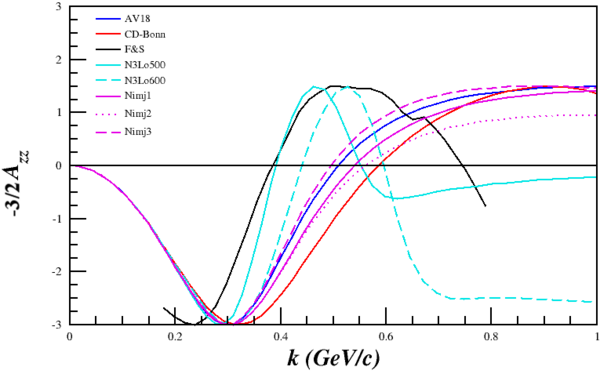
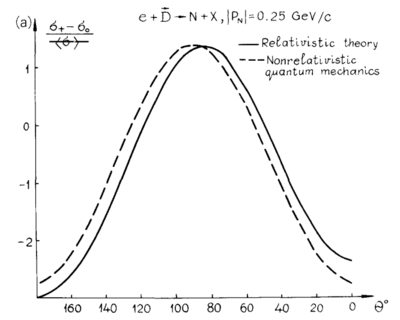
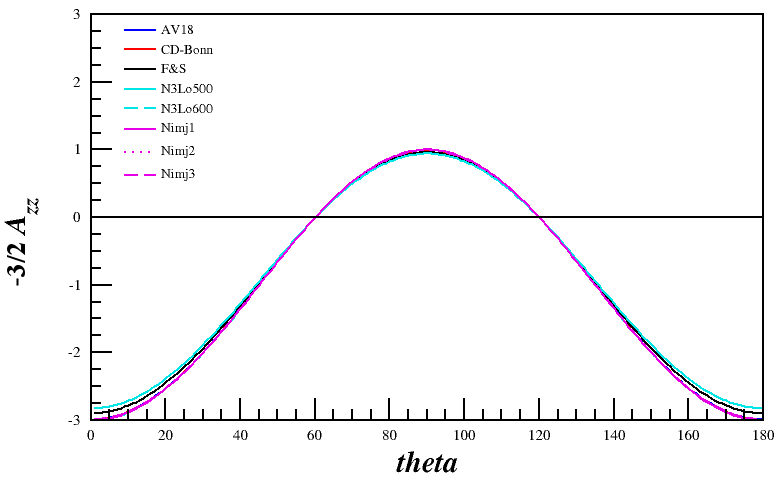
This would make their Fig. 7.5 from their 1988 report simply <math>A_{zz} = r(\pm 1,k)-r(0,k)</math> for D(e,e'p) with p at 180deg, which can also be reproduced.
Angular Dependence
One of the on-going issues I've been having is defining the kinematic directions the same as F&S. Following the convention
With the light-cone variables being used, I believe that <math>k_1 = k_{\perp} = \sqrt{k_x^2+k_y^2},~~k_2=0,~~k_3=k_z</math>. This lets me recreate their angular distribution in the 1988 report's Fig. 7.6
Note that my assumption for the section above, with the knocked-out proton going at 180deg, as <math>\sin(\pi)=0 \rightarrow k_1=k_2=0, ~\cos(\pi)=1 \rightarrow k_3=k</math> would hold.
Azz for D(e,e')
In order to find the inclusive D(e,e') Azz, we would simply integrate over all possible angles of the knocked-out nucleon. This gives
On-going Issues
One thing that I'm not entirely sure of at the moment is how to go from <math>k \rightarrow x_{Bj}</math>. I'm also going to ask Mark if he wouldn't mind checking my above work.