Difference between revisions of "Elong-15-04-07"
| Line 1: | Line 1: | ||
| − | |||
| − | |||
=Relating t20 and Azz= | =Relating t20 and Azz= | ||
Revision as of 07:57, 24 April 2015
Relating t20 and Azz
The Boden '91 paper, the only existing t20 measurement taken with a solid ND3 target, does a nice job of describing the relationship between the measured ratio and t20. Eq. 1 describes their ratio,
<math>R_{exp}=\frac{d\sigma_p}{d\sigma_u}=1+P_{zz} \left( \frac{d\sigma_T-d\sigma_u}{d\sigma_u} \right) = 1+P_{zz} \left( R_T-1 \right) </math>
<math>R_T-1 = \frac{1}{P_{zz}} \left( \frac{d\sigma_p}{d\sigma_u} -1 \right).</math>
This matches closely to our Azz,
<math>A_{zz}=\frac{2}{fP_{zz}}\left( \frac{d\sigma_p}{d\sigma_u}-1\right), </math>
where the <math>f=1</math> in the Boden result, since they are tagging deuterons and have negligible contamination.
The two are related by
<math>R_T-1=\frac{1}{2}A_{zz}.</math>
Later on in the paper, <math>(R_T-1)</math> is related to t20 by neglecting the (small) magnetic contributions to get
<math>t_{20}=-\sqrt{8}(R_T-1),</math>
which we can relate to our Azz above by
<math>t_{20}=-\sqrt{2}A_{zz}.</math>
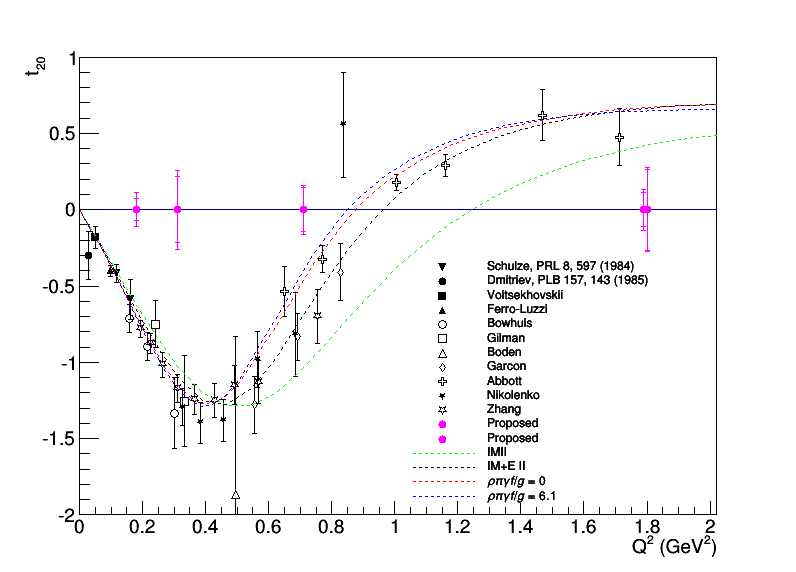
Adjusting the uncertainties calculated last week, which were simply Azz at x=2, by
<math>\delta t_{20} = \sqrt{2}\delta A_{zz},</math>
we get the plot below.
An important caveat related to the first topic above: The Boden measurement tags deuterons with a hadron scattering angle of ~70 deg, which is where each t20 measurement was taken or rotated to on the plot above.