Elong-13-05-01

Cross-Section Issue - Fixed

From looking at the dilution factor, f, I found a problem with how the cross-sections were calculated. We know that, naively,
<math>f=\frac{N_{D}}{(N_{D}+N_{N}+N_{He})} = \frac{t\cdot R_{D}}{(t\cdot R_{D}+t\cdot R_{N}+t\cdot R_{He})} = \frac{R_{D}}{(R_{D}+R_{N}+R_{He})} \approx \frac{N_{D}}{N_{D}+N_{N}}\approx \frac{3\sigma_{D}}{3\sigma_{D}+\sigma{N}}\approx \frac{3\cdot 2}{3\cdot 2 + 14}\approx 6/20=0.3</math>.

Originally, I was (wrongly) using <math>\frac{d^2\sigma^u}{d\Omega dE'} = \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{X}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]</math>

where X = nucleus and <math>\left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}}=\frac{Z^2 \alpha^2 \hbar^2 c^2}{4E^2\sin^4\left( \frac{\theta}{2} \right)}\cos^2\left( \frac{\theta}{2} \right)</math>.
This gave <math>f \approx 0.062</math>.

The problem came from using a nuclear Mott cross-section but a nucleon structure cross-section. To fix this, I first found the Mott cross-section for a proton,
<math>\left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}}=\frac{1^2 \alpha^2 \hbar^2 c^2}{4E^2\sin^4\left( \frac{\theta}{2} \right)}\cos^2\left( \frac{\theta}{2} \right)</math>,

and then multiplied that by the structure cross-section at the total number of nucleons,

<math>\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{X}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]</math>.

This gave <math>f \approx \frac{3\sigma_{D}}{3\sigma_{D}+\sigma{N}} \approx 0.29</math>, as expected.

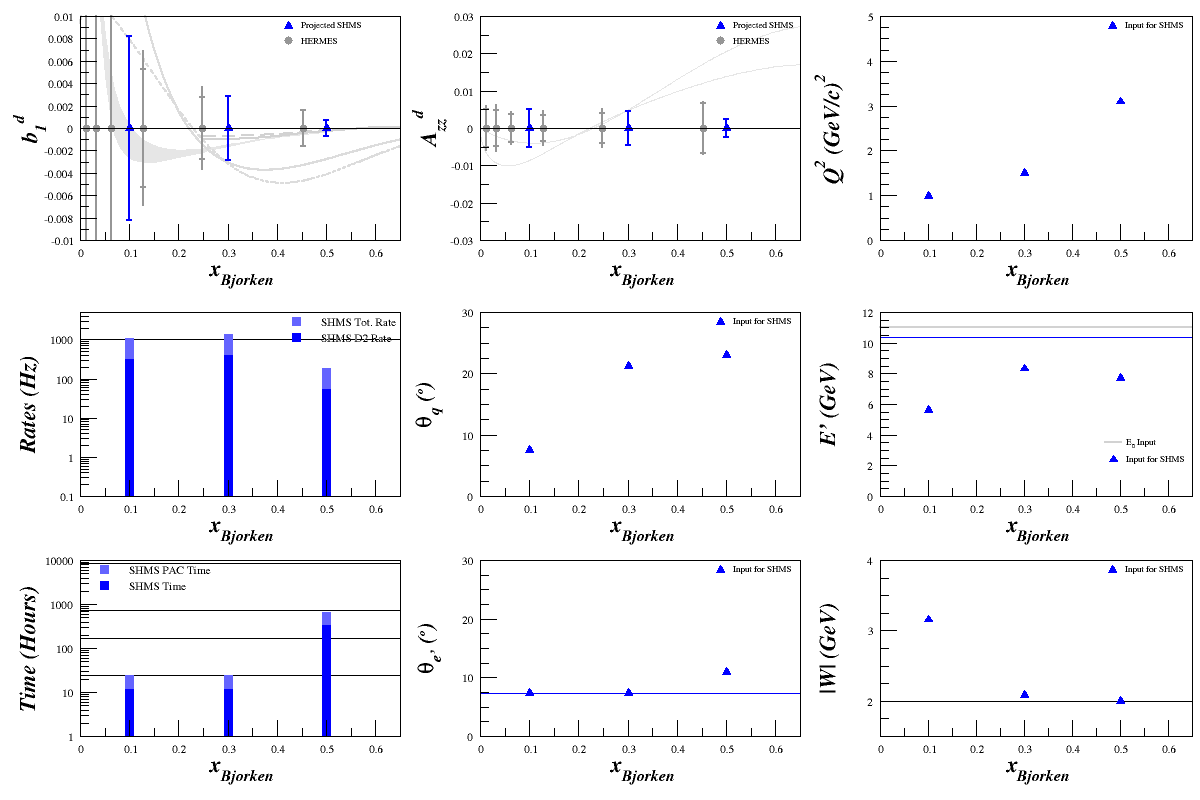
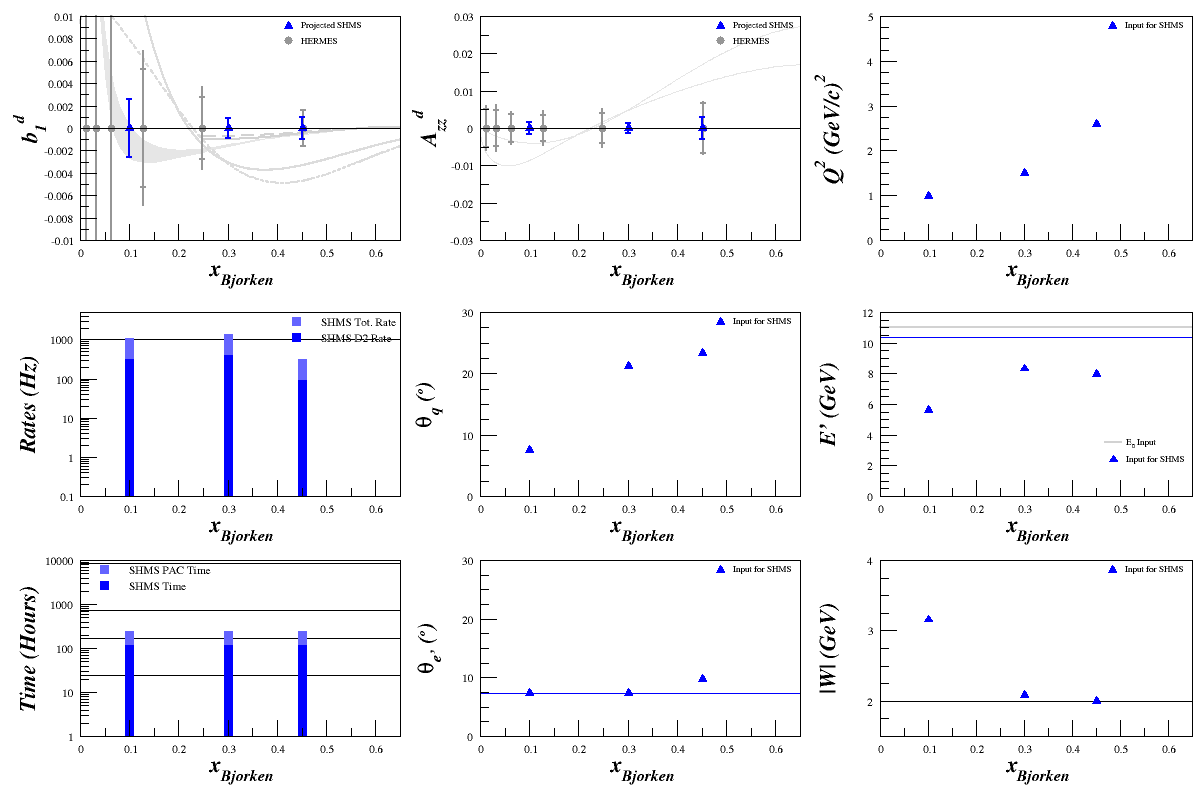
Plugging all this into the rates code gave (NOTE: The error on b₁^d is wrong, as discussed below):

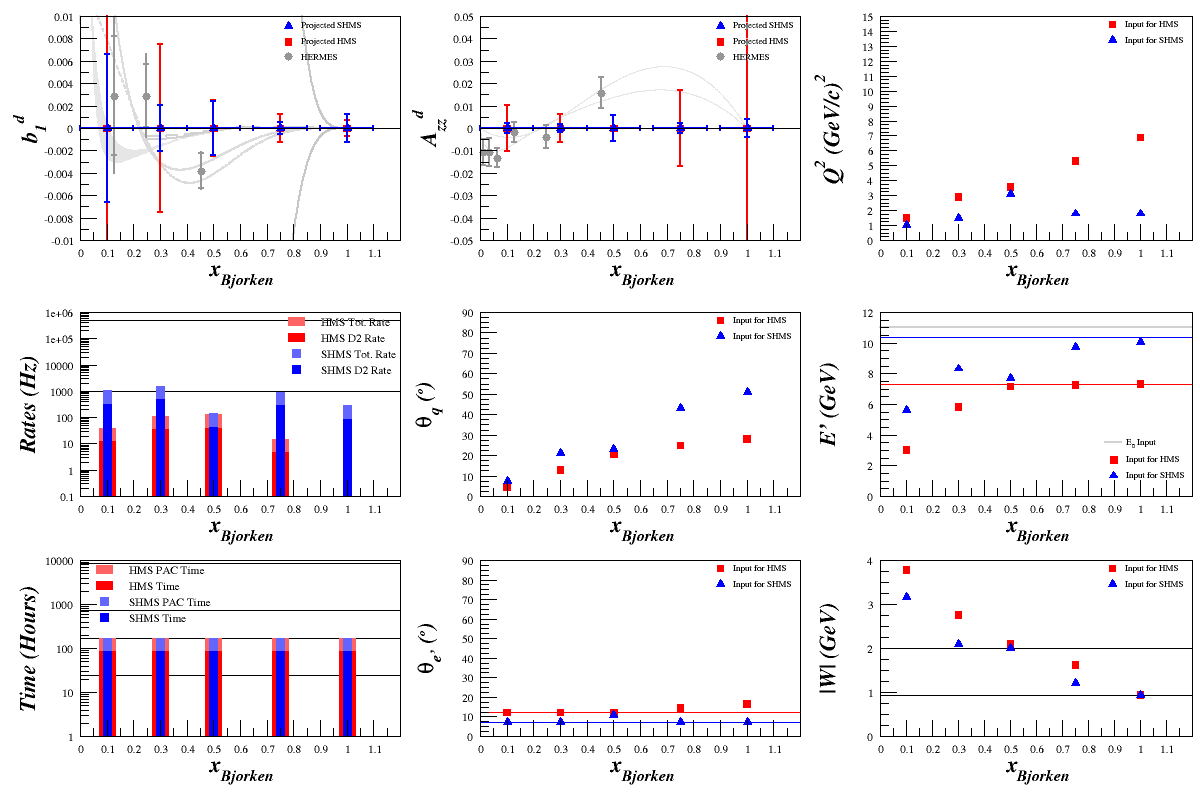
Matching HERMES F₁^d, dA_zz^d, and db₁^d

I wanted to double-check the code against the HERMES data, but this required a few extra steps. First, using the values for <math>A_{zz}^d</math> and <math>b_{1}^d</math> that they measured, along with the formula <math>b_1^d = -\frac{3}{2}A^d_{zz}F^d_1</math>, I found what they were using for <math>F^d_1</math>. The <math>F^d_1</math> they're using is per nucleon, and for HERMES' two highest x points (the rest are inaccessible to the Bosted code because for 0.012<x<0.063, 16.75<W²<42.87, which is outside the W range that the code can handle) they match the code relatively well:

<x>	Q 2	HERMES <math>F_1^d</math>	Bosted <math>\frac{F_1^d}{A_d}</math>
0.128	2.33	1.018	0.620 (Outside Bosted "Good" range)
0.248	3.11	0.496	0.486
0.452	4.69	0.161	0.171

This means that the way I was calculating the error <math>\delta b_1^d=\frac{3}{2}\delta A_{zz}^d F_1^d</math> was off by a factor of <math>A_d=2</math>. This was corrected.

I also played a bit with the statistics, trying to match the HERMES results. However, that's a very quick estimate of trying to use the SMHS to copy the HERMES detector, and so the entire link should be taken with a huge grain of salt.

Fixed Rates Code

Now that everything is working as it should, I've replotted the lowest three <x> points where we can spend 4 weeks taking data. Since the HMS can't get into the range we need for <math>F_1^d</math>, I've removed those calculations. The results (on a re-worked scale to emphasize their value) are:

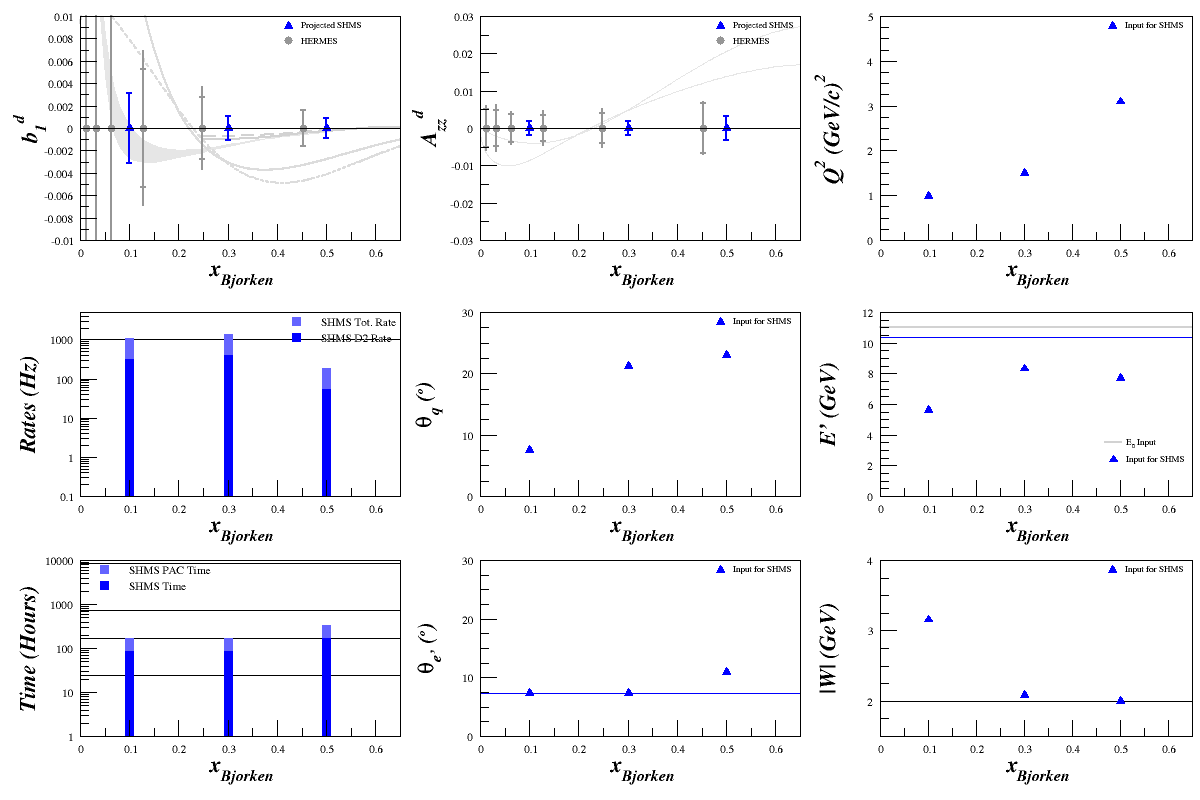
Where

Target Material	ND3
Target Length	3 cm
fdil	Calculated ~ 0.3
pf	0.65
Pzz	20%
E0	11 GeV
xBjorken	0.1, 0.3, 0.5
Q2	Variable
θq	Calculated
θe'	Calculated
E'	Calculated
W	Calculated

A_zz Formalism

Just for clarification, I'm using the formalism as described below.

Target Material = ND3

<math>z_{\mathrm{tgt}} = 3\mathrm{ cm}</math>

<math>p_f = 0.65</math>

<math>P_{zz} = 20\%</math>

<math>N_{A} = 6.0221413\cdot 10^{23}</math>

<math>\rho_{\mathrm{He}} = 0.1412 \mathrm{g/cm}^3</math>

<math>M_{\mathrm{He}} = 4.0026 \mathrm{g/mole}</math>

<math>\rho_{\mathrm{ND}_3} = 1.007 \mathrm{g/cm}^3</math>

<math>M_{\mathrm{ND}_3} = 20 \mathrm{g/mole}</math>

<math>I_{\mathrm{beam}} = 0.115 \mathrm{\mu A}</math>

<math>\delta F_1^d = 5\%</math>

(1)	<math>R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}}\left( \frac{d^2\sigma_{\mathrm{He}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{N}}\left( \frac{d^2\sigma_{\mathrm{N}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{D}}\left( \frac{d^2\sigma_{\mathrm{D}}}{d\Omega dE'}\right) \right]</math>
(2)	<math>R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}}\left( \frac{d^2\sigma_{\mathrm{He}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{N}}\left( \frac{d^2\sigma_{\mathrm{N}}^u}{d\Omega dE'}\right) + \mathcal{L}_{\mathrm{D}}\left( \frac{d^2\sigma_{\mathrm{D}}^u}{d\Omega dE'}\left[ 1 + \frac{1}{2}P_{zz}A_{zz}^d \right]\right) \right] </math>
(2a)	<math>R_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz}A_{zz}^d \right) \right] </math>

where

(3)	<math>\mathcal{A} = \left( \Delta\Omega \Delta E' \right)</math>
(4)	<math>\mathcal{L}_{\mathrm{He}} = \left[ \mathcal{N}_A \frac{\rho_{\mathrm{He}}}{M_{\mathrm{He}}}\left(1 - p_f\right) \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}</math>
(5)	<math>\mathcal{L}_{\mathrm{N}} = \left[ \mathcal{N}_A \frac{\rho_{\mathrm{ND}_3}}{M_{\mathrm{ND}_3}} p_f \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}</math>
(6)	<math>\mathcal{L}_{\mathrm{D}} = 3\left[ \mathcal{N}_A \frac{\rho_{\mathrm{ND}_3}}{M_{\mathrm{ND}_3}} p_f \right] \cdot \left( \frac{I_{\mathrm{beam}}}{e} \right) \cdot z_{\mathrm{tgt}}</math>
(7)	<math>\sigma^u_X = \frac{d^2\sigma^u_X}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]</math>
(8)	<math>\left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}}=\frac{1^2 \alpha^2 \hbar^2 c^2}{4E^2\sin^4\left( \frac{\theta}{2} \right)}\cos^2\left( \frac{\theta}{2} \right)</math>
(9)	<math>\sigma_D = \frac{d^2\sigma_{\mathrm{D}}}{d\Omega dE'} = \frac{d^2\sigma_{\mathrm{D}}^u}{d\Omega dE'}\left[ 1 + \frac{1}{2}P_{zz}A_{zz}^d \right] </math>

Then

(10)	<math>R^+_{\mathrm{Total}} - R^-_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz}^+ A_{zz}^d \right) \right] - \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz}^- A_{zz}^d \right) \right] </math>
(10a)	<math>R^+_{\mathrm{Total}} - R^-_{\mathrm{Total}} = \mathcal{A}\mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u \frac{1}{2}A_{zz} \left[ P_{zz}^+ - P_{zz}^- \right]</math>
(11)	<math>R^+_{\mathrm{Total}} + R^-_{\mathrm{Total}} = \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz}^+ A_{zz}^d \right) \right] + \mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left( 1 + \frac{1}{2}P_{zz}^- A_{zz}^d \right) \right] </math>
(11a)	<math>R^+_{\mathrm{Total}} + R^-_{\mathrm{Total}} = 2\mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u \right] + \mathcal{A}\mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u\left[ \frac{1}{2}P_{zz}^+ A_{zz}^d + \frac{1}{2}P_{zz}^- A_{zz}^d \right] </math>

If we assume that <math>P_{zz}^+ = -P_{zz}^- = P_{zz}</math>, then

(12)	<math>R^+_{\mathrm{Total}} - R^-_{\mathrm{Total}} = \mathcal{A}\mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u A_{zz} P_{zz}</math>
(13)	<math>R^+_{\mathrm{Total}} + R^-_{\mathrm{Total}} = 2\mathcal{A}\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u \right] </math>
(14)	<math>A_{\mathrm{meas}} = \frac{R^+_{\mathrm{Total}} - R^-_{\mathrm{Total}}}{R^+_{\mathrm{Total}} + R^-_{\mathrm{Total}}}</math>
(14a)	<math>A_{\mathrm{meas}} = \frac{\mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u A_{zz} P_{zz}}{2\left[ \mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u \right]}</math>
(14b)	<math>A_{\mathrm{meas}} = \left( \frac{\mathcal{L}_{\mathrm{D}}\sigma_{\mathrm{D}}^u}{\mathcal{L}_{\mathrm{He}} \sigma_{\mathrm{He}}^u + \mathcal{L}_{\mathrm{N}} \sigma_{\mathrm{N}}^u + \mathcal{L}_{\mathrm{D}} \sigma_{\mathrm{D}}^u} \right) \frac{ A_{zz} P_{zz}}{2}</math>
(14c)	<math>A_{\mathrm{meas}} = f \frac{ A_{zz} P_{zz}}{2}</math>
(15)	<math>A_{zz} = \frac{2 }{f \cdot P_{zz}}A_{\mathrm{meas}}</math>

In order to get the uncertainty, we'd use

(16)	<math>\delta A_{zz} = \sqrt{\left( \frac{\partial A_{zz}}{\partial A_{\mathrm{meas}}} \delta A_{\mathrm{meas}} \right)^2 + \left( \frac{\partial A_{zz}}{\partial f} \delta f \right)^2 + \left( \frac{\partial A_{zz}}{\partial P_{zz}} \delta P_{zz} \right)^2 }</math>
(16a)	<math>\delta A_{zz} = \sqrt{\left( \delta A_{zz}^{\mathrm{Stat}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Dil}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Pol}} \right) ^2 }</math>
(16b)	<math>\delta A_{zz} = \sqrt{\left( \delta A_{zz}^{\mathrm{Stat}} \right) ^2 + \left( \delta A_{zz}^{\mathrm{Sys}} \right) ^2 }</math>

Ignoring <math>\delta A_{zz}^{\mathrm{Sys}}</math> for now (and in all of the plots I'm showing), then

(17)	<math> \delta A_{zz}^{\mathrm{Stat}} = \frac{\partial A_{zz}}{\partial A_{\mathrm{meas}}} \delta A_{\mathrm{meas}} = \frac{2}{f\cdot P_{zz}} \delta A_{\mathrm{meas}} = \frac{2}{f\cdot P_{zz}}\frac{1}{\sqrt{N_{\mathrm{Total}}}} </math>
(17a)	<math> \delta A_{zz}^{\mathrm{Stat}} = \frac{2}{f\cdot P_{zz}\sqrt{t\cdot R_{\mathrm{Total}}}} </math>

Using the same formalism that HERMES used (which defines <math>F_{1_{\mathrm{HERMES}}}^d = \frac{(1 + Q^2/\nu^2)F_2^d}{2x(1+R)}</math> with <math>F_2^d=\frac{F_2^p + F_2^n}{2}</math> as a per nucleon quantity, which corresponds to the Bosted that uses per nucleus by <math>F_{1_{\mathrm{HERMES}}}^d = \frac{F_{1_{\mathrm{Bosted}}}^d}{A_{\mathrm{D}}} = \frac{F_1^d}{2}</math> -- as described above), we can extract <math>b_1^d</math> and its uncertainty by

(18)	<math> b_1^d = - \frac{3}{2}A_{zz} \left( \frac{F_1^d}{A_{\mathrm{D}}} \right)= - \frac{3}{2}A_{zz} \left( \frac{F_1^d}{2} \right)</math>
(19)	<math> \delta b_1^d =\sqrt{ \left(\frac{\partial b_1^d}{\partial A_{zz}} \delta A_{zz} \right)^2 + \left(\frac{\partial b_1^d}{\partial F_1^d} \delta F_1^d \right)^2 }</math>
(19a)	<math> \delta b_1^d =\sqrt{ \left[ - \frac{3}{2} \left( \frac{F_1^d}{2} \right)\delta A_{zz} \right]^2 + \left[ - \frac{3}{2} A_{zz} \left( \frac{1}{2} \right)\delta F_1^d \right]^2 }</math>

Playing with 30 Days

The most interesting point seems to be at <x> ~ 0.5. We can focus the majority of our time there (28 days for <x>=0.5, and 1 day for <x>=0.1 and 0.3), and still get reasonable results for two more points.

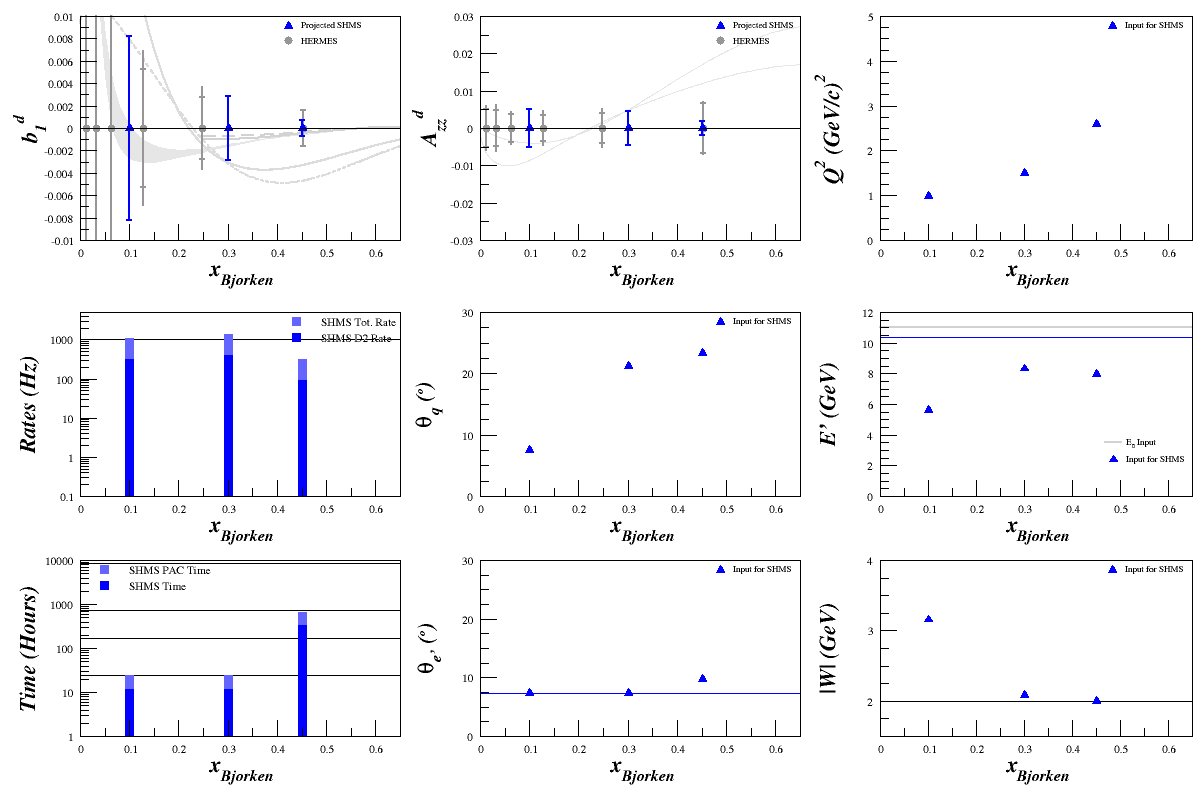
We can do even better if we sit directly on <x> = 0.452 (28 days for <x>=0.452, and 1 day for <x>=0.1 and 0.3), since that lets us pull the angle down a bit and thus get a higher rate:

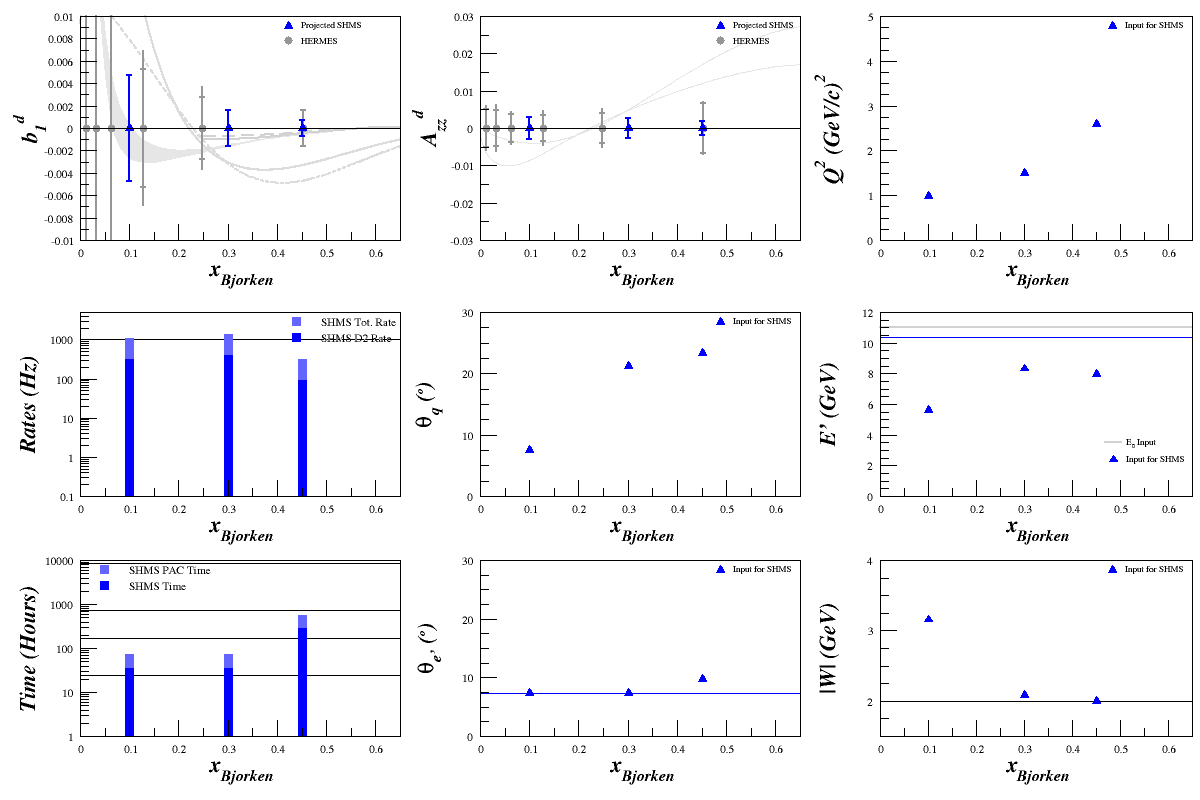
If we wanted to do better than HERMES for all points, we could do 24 days for <x>=0.5, and 3 days for <x>=0.1 and 0.3

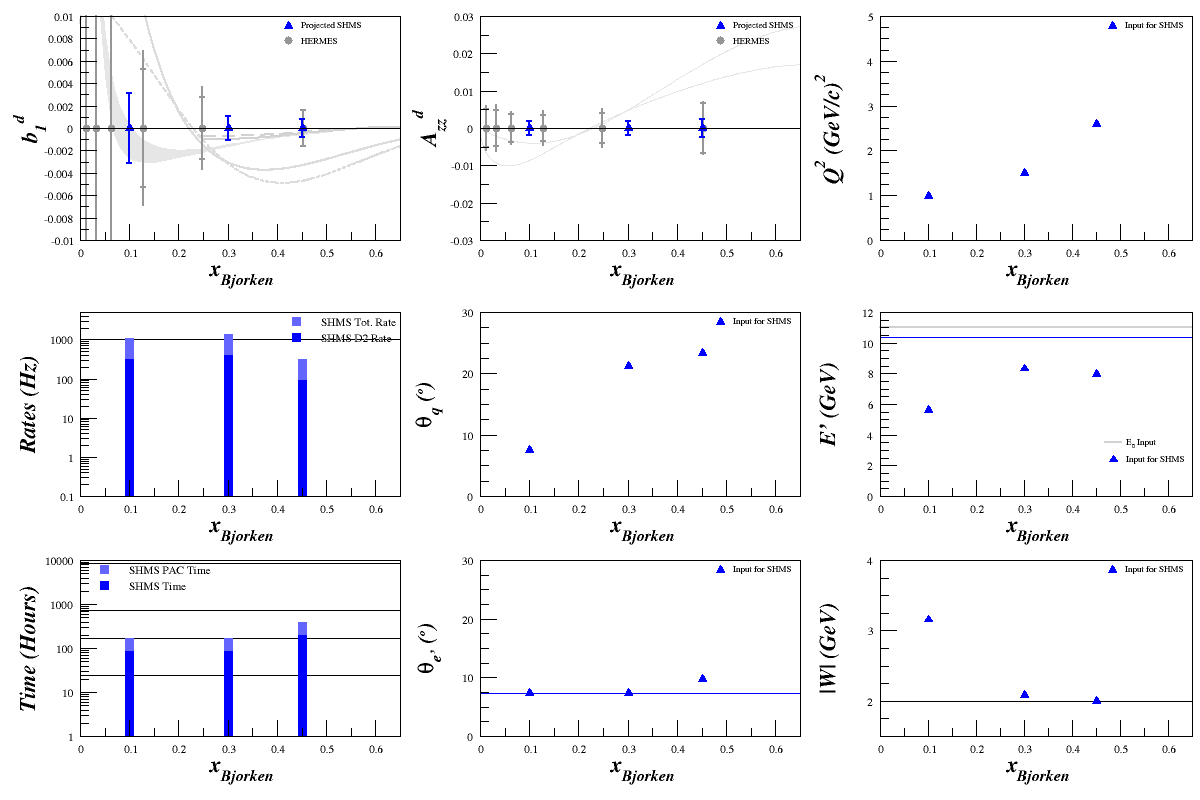
If we wanted to do a lot better than HERMES for all points, we could do 16 days for <x>=0.5, and 7 days for <x>=0.1 and 0.3

If we wanted to split our time up evenly, we could do 10 days for <x>=0.5, 0.3, and 0.1