Elong-13-09-30
Diluction Factor Comparisons
First Pass
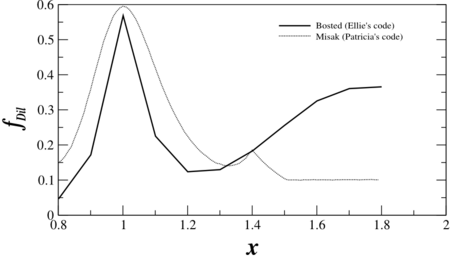
I've been using the Bosted model to extract the dilution factor, but I hadn't previously plotted it against x. This was prompted when Patricia sent me a plot that she had created as she's working with a new model from Misak. The comparison for the new Azz, using the kinematics from the SHMS, is:
(Note: The kinematics for this are the same as the SHMS's highest x point for b1, not Azz as I originally thought)
The most important difference comes in the SRC (high-x) region, where one model diverges and the other hits a plateau. More work needs to be done to double-check the cross sections and find out why one model seems to have a much wider peak than the other. One possibility is that the Bosted model (running on my code) is currently only being generated for each point that Azz is. I'll do a more intensive scan over x next week.
Larger x Range for Bosted
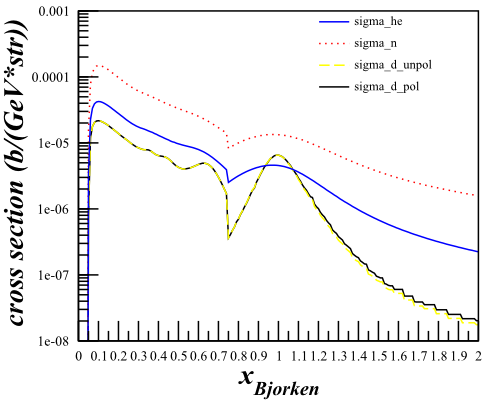
Using the kinematics for the SHMS (<math>E_{\mathrm{beam}}=6.60\mathrm{~GeV}</math>, <math>E'=6.07\mathrm{~GeV}</math>, <math>\theta_{e'}=9.51^{\circ}</math>) to calculate the cross section and scanning over <math>0<x<2</math> with 200 bins, the Bosted cross-sections come out to:
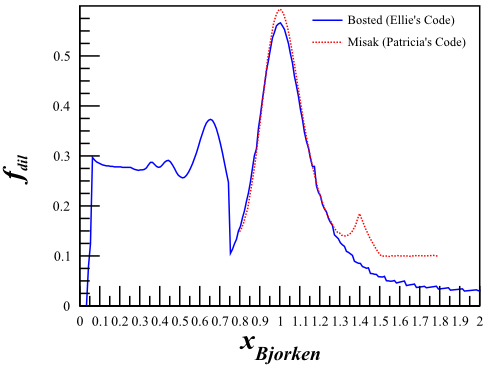
and the dilution, compared with the Misak model, comes out to:
There is a discontinuity at <math>x=0.75</math>, which is caused by a (somewhat arbitrary) switch from Bosted's DIS code to his QE code at thaht point. The dilution factor is also different than shown above, because in the first plot shown on this page I accidentally left the kinematics set to the b1 experiment's (and not the Azz one).
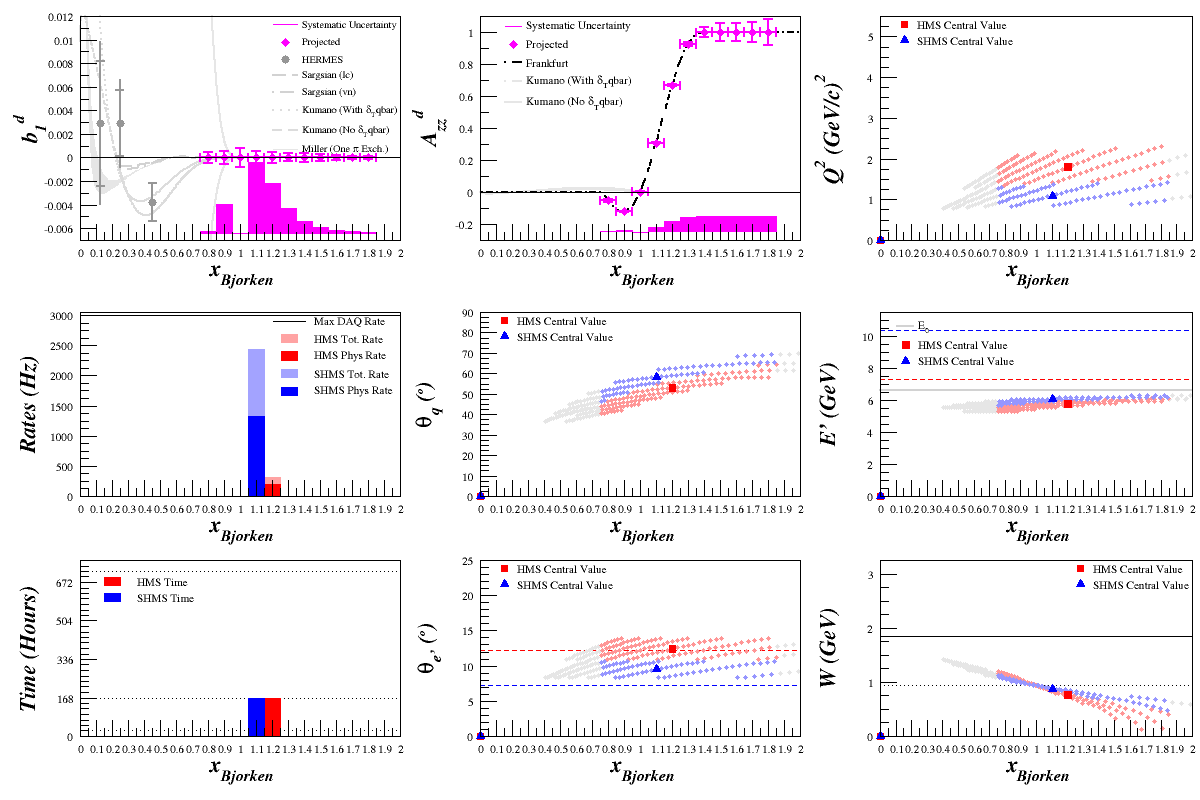
Changes to Azz Statistics
Previously, the dilution factor was assumed to be about 0.3. since this is no longer the case, and the dilution factor has been changed to that shown in the Bosted plot above, the statistics for Azz (particularly in the high-x range) get larger.