Elong-14-04-16

Deuteron Polarization

Being a spin-1 particle, the deuteron has three spin sub-states that can be filled: $m_J=+1,~m_J=0,~m_J=-1$. For a given quantity of deuterons, the polarization is measured based on the population $p_m$ in each substate. The population is defined as

$p_m=\frac{N_m}{N_1+N_0+N_{-1}}$

where $N_m$ is the number of deuterons in a given substate. In a system of pure deuterons, the normalization of the populations is

$p_1+p_0+p_{-1}=1$.

Vector polarization depends only on the $m_J=\pm 1$ populations, such that

$P_z = p_1 - p_{-1}~$.

It has a range of $-1<P_z<1~$.

If the $m_1$ state is filled, then $p_1=1,~p_{-1}=0,~p_0=0$ and $P_z=1~$.

If the $m_{-1}$ state is filled, then $p_1=0,~p_{-1}=1,~p_0=0$ and $P_z=-1~$.

If the $m_0$ state is filled, then $p_1=0,~p_{-1}=0,~p_0=1$ and $P_z=0~$.

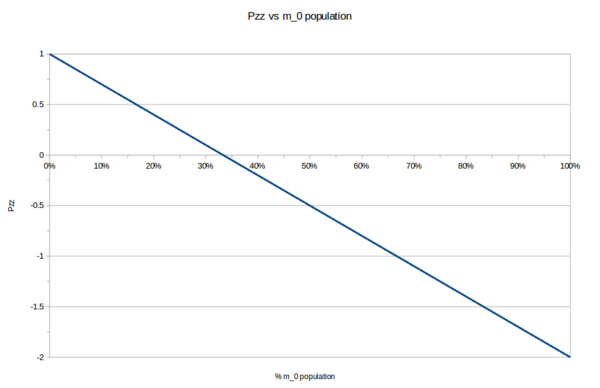
Tensor polarization depends on the combined $m_J=\pm 1$ populations, as well as the $m_J=0$ population such that

$P_{zz} = (p_1 + p_{-1}) - 2p_0~$.

It has a range of $-2<P_{zz}<1~$.

If the $m_1$ and $m_{-1}$ states are filled, then $(p_1 + p_{-1})=1,~p_0=0$ and $P_{zz}=1~$.

If the combined $m_1$ and $m_{-1}$ states equal the $m_0$ state, then $(p_1+p_{-1})=0.5,~p_0=0.5$ and $P_{zz}=-0.5~$

If the $m_0$ state is filled, then $(p_1 + p_{-1})=0,~p_0=1$ and $P_{zz}=-2~$.

Or, in terms of an overly-simplistic animation,

Deuteron Shape

From the video made by S.C. Pieper, et al., I extracted the tensor and vector polarization frames and made repeating videos of each. When we vector-polarize or tensor-polarize, the probability densities for the deuteron look like:

m_s=±1	m_s=0

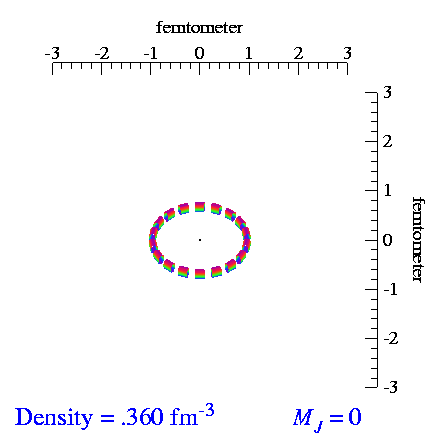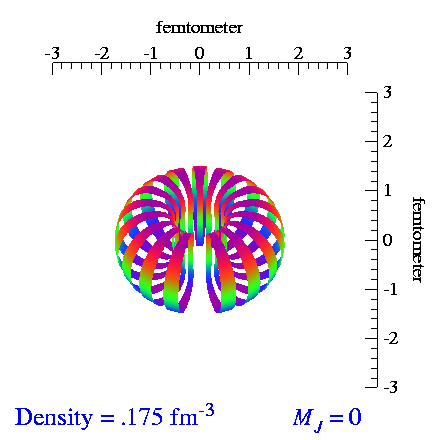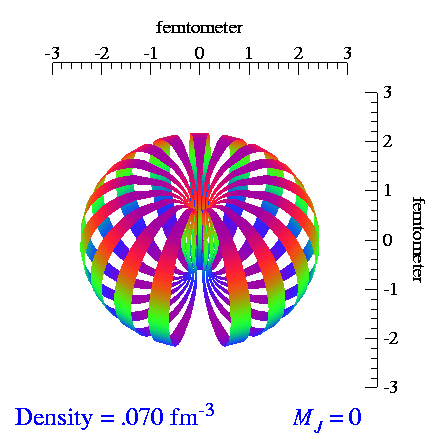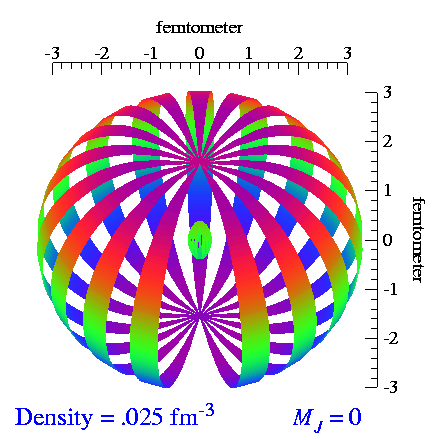
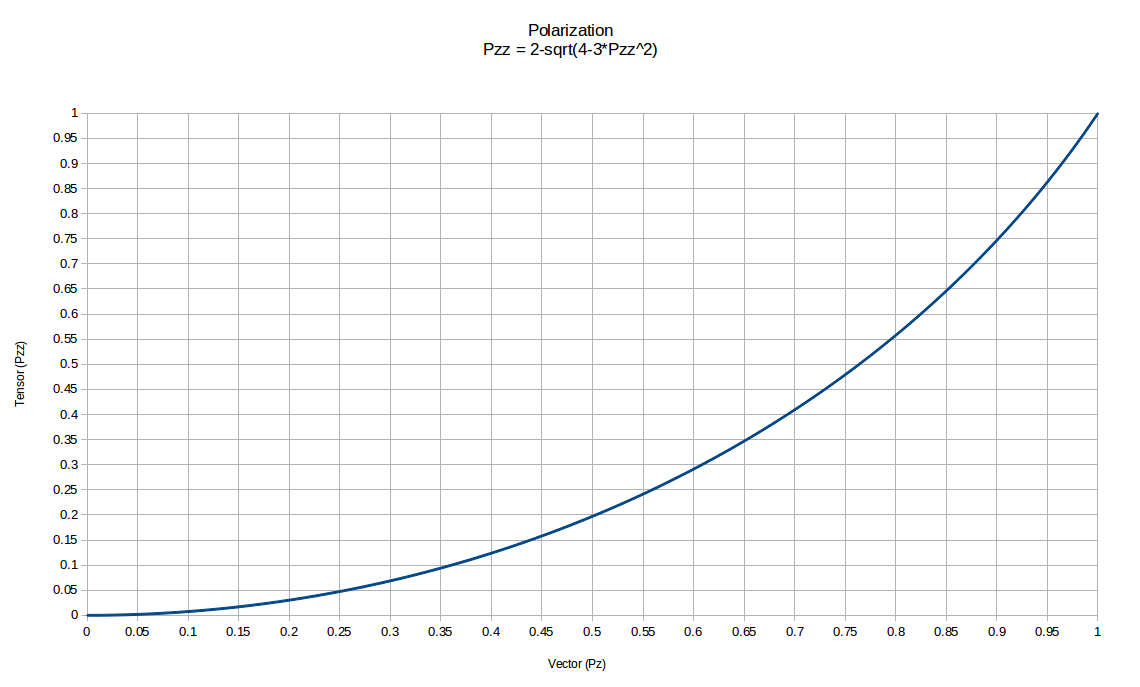
Tensor Polarization Relation to Vector Polarization

Tensor polarization is related to the vector polarization by $P_z=2-\sqrt{4-3P_{zz}^2}$

Deuteron States

From basic quantum mechanics, we know that the possible states for 2 nucleons are

the isospin singlet with S=0:

$|\uparrow \downarrow> - |\downarrow \uparrow>$ with $m_s=0$, $L=1$

and the isospin triplet with S=1:

$|\uparrow \uparrow>$ with $m_s=+1$, $L=0$

$|\uparrow \downarrow> + |\downarrow \uparrow>$ with $m_s=0$, $L=1$

$|\downarrow \downarrow>$ with $m_s=-1$, $L=2$

For the deuteron, $J=1$ and $P=+1$. This kills both of the $m_s=0$ states, since they cannot simultaneously have $J=1$ and $P=+1$ since $P=(-1)^L$.

This leaves only two possible states:

$|\uparrow \uparrow>$ with $m_s=+1$, $L=0$

$|\downarrow \downarrow>$ with $m_s=-1$, $L=2$

Angular Momentum Analysis

Now, let's look at each of these a bit more indepth according to their angular momentum components

J	$m_J$	L	$m_L$	S	$m_S$	$\pi = -1^L$	T	$^{2S+1}L_J$
0	0	0	0	1	0	+	1	$^1 S_0$
1	±1	0	0	1	±1	+	0	$^3 S_1$
1	1	2	1	1	0	-	0	$^1 P_1$
1	0	2	-1	1	1	-	1	$^3 P_0$
1	0	2	1	1	-1	-	1	$^3 P_0$
1	1	2	1	1	0	-	1	$^3 P_1$
1	2	2	1	1	1	-	1	$^3 P_2$
1	2	2	2	1	0	+	1	$^1 D_2$
1	1	2	2	1	-1	+	0	$^3 D_1$
1	-1	2	-2	1	+1	+	0	$^3 D_1$
3	3	2	2	1	1	+	0	$^3 D_2$
3	3	2	2	1	1	+	0	$^3 D_3$

When we remove all of the states that can't exist, we're left with two mentioned in the last section:

J	$m_J$	L	$m_L$	S	$m_S$	$\pi = -1^L$	T	$^{2S+1}L_J$
1	±1	0	0	1	±1	+	0	$^3 S_1$
1	1	2	2	1	-1	+	0	$^3 D_1$
1	-1	2	-2	1	+1	+	0	$^3 D_1$

S and D States

A variety of models have looked at the wavefunction from the S- and D-states.

File:2014-04-24-deuteron-wavefunction-s-d-states.pdf

--E. Long 19:53, 24 April 2014 (UTC)