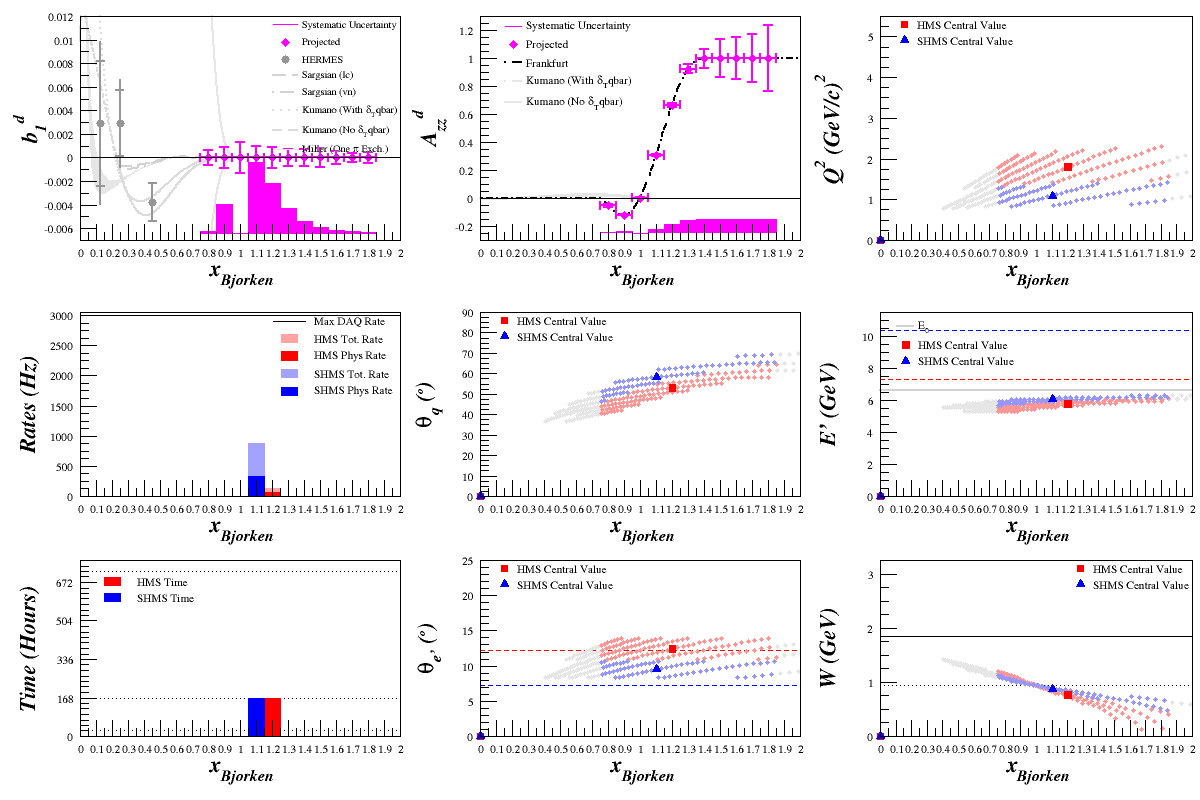
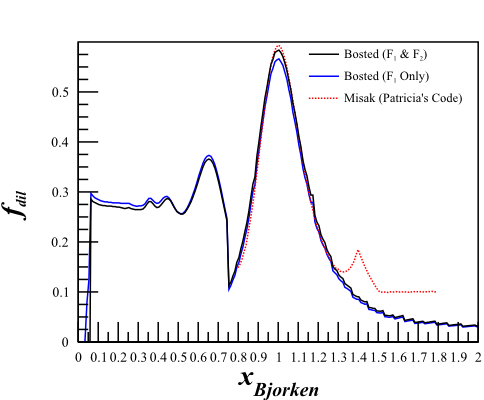
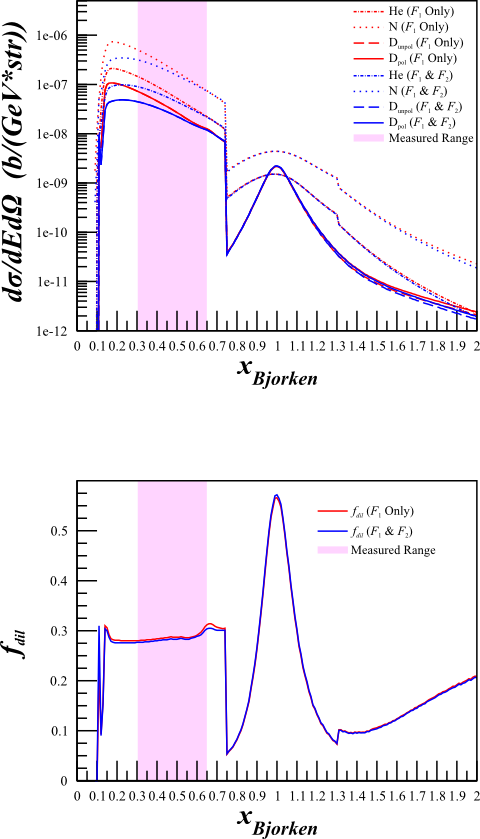
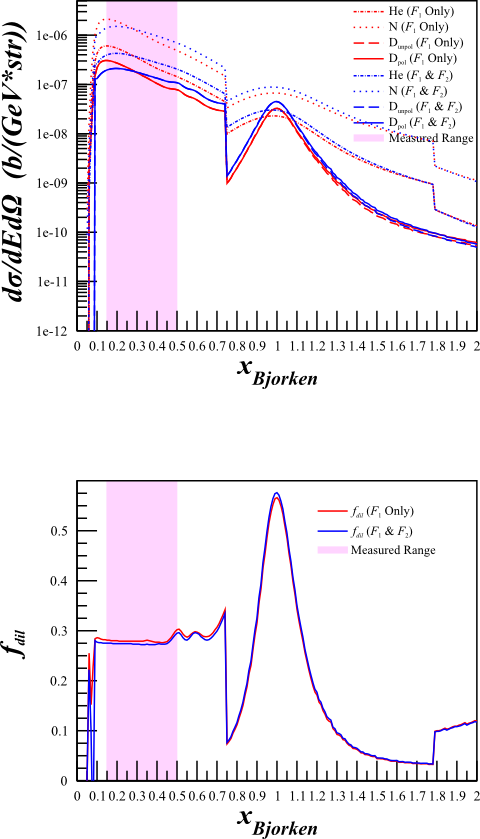
Elong-13-10-01

Cross Section Calculation

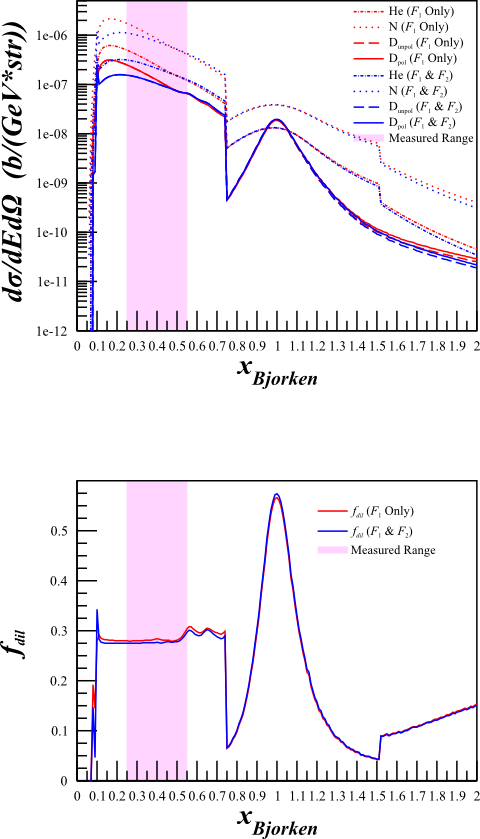
For previous calculations, I was using a simplified version of the cross-section where it was assumed that <math>F_2=2x\cdot F_1</math>, such that

<math>\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\right]\cdot \left[\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{Q^2 }{2\nu^2} \right] </math>.

Since we're in a region that isn't DIS, I thought that the difference may be important so I incorporated <math>F_2</math> from Bosted and removed the assumption:

<math>\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]</math>.

This increased the statistical uncertainty, particularly in the high-x region. It also lowered the rates dramatically, which gives us some room to play around with a lower <math>Q^2</math>.

Although this changes the cross sections quite a bit,

<math>F_1 \mathrm{~Only}</math>	<math>F_1\mathrm{~and~}F_2</math>

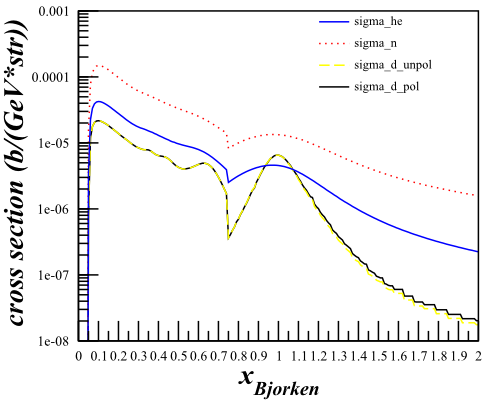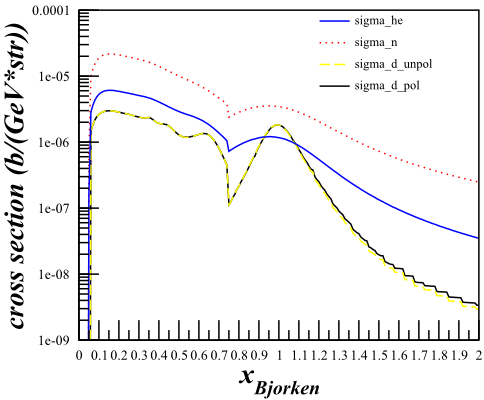
The dilution factor is nearly identical.

Cross Section Check for b1

To see if this could cause a problem for the b1 statistics, I did a study of the effects of changing the cross section calculation from the simplified to the full for the b1 kinematics.

HMS <math>\theta_{e'}=12.50^{\circ}</math> <math>E'=7.31\mathrm{~GeV}</math>	SHMS 1 <math>\theta_{e'}=7.35^{\circ}</math> <math>E'=6.80\mathrm{~GeV}</math>	SHMS 2 <math>\theta_{e'}=8.96^{\circ}</math> <math>E'=7.45\mathrm{~GeV}</math>	SHMS 3 <math>\theta_{e'}=9.85^{\circ}</math> <math>E'=7.96\mathrm{~GeV}</math>

Cross Section Check for Azz

Same as the section above, looking at the difference between the simplified cross section using only <math>F_1</math> and the full cross section using both <math>F_1</math> and <math>F_2</math>, but for the Azz kinematics.

HMS <math>\theta_{e'}=12.45^{\circ}</math> <math>E'=5.80\mathrm{~GeV}</math>	SHMS <math>\theta_{e'}=9.51^{\circ}</math> <math>E'=6.07\mathrm{~GeV}</math>

--E. Long 21:20, 1 October 2013 (UTC)