Azz Re-Optimization
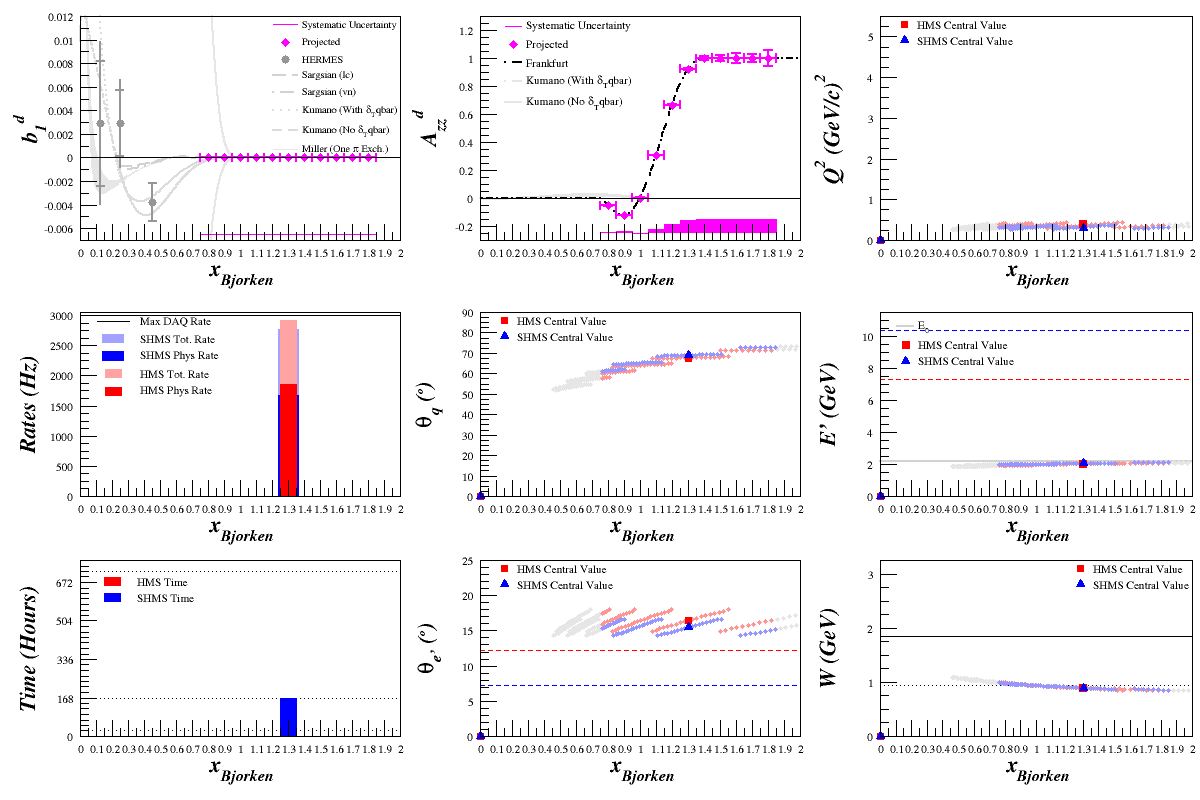
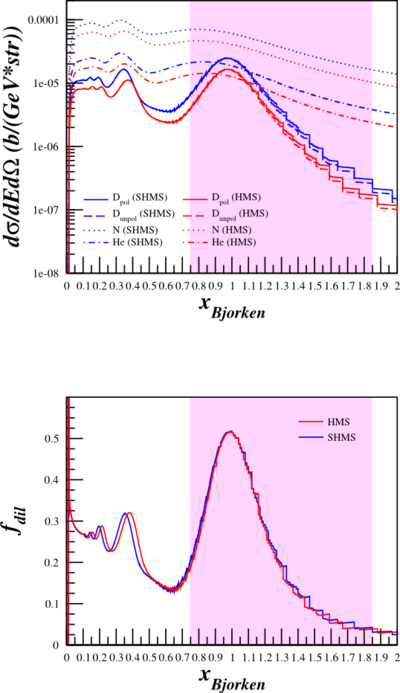
Using the Bosted code, which now uses the complete cross-section with both QE and DIS parts, has been checked against previous data, and uses the full dilution factor, I've gone back through beam energies of 6.6, 4.4, and 2.2 GeV and optimized the physics rates while keeping the total rates below the DAQ maximum (without prescales) of 3kHz. For each of the uncertainty estimates below, the dilution factor used was calculated from the SHMS cross-sections.
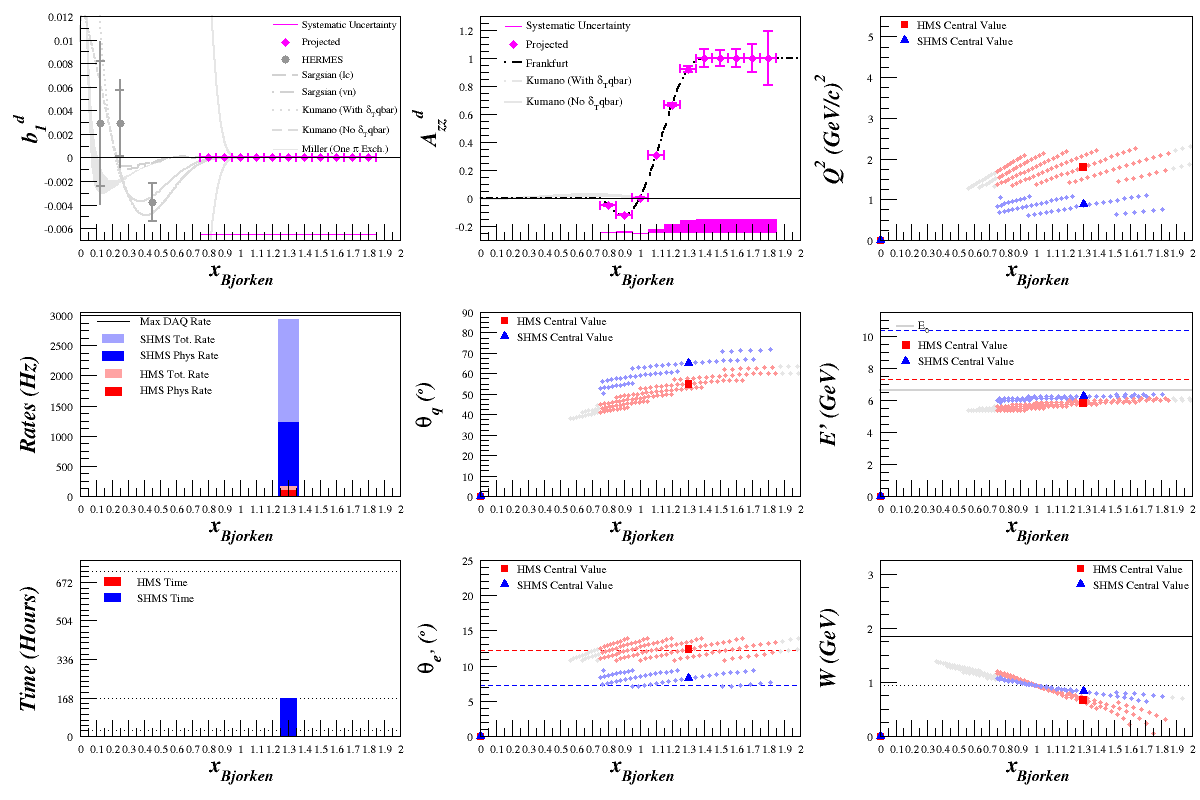
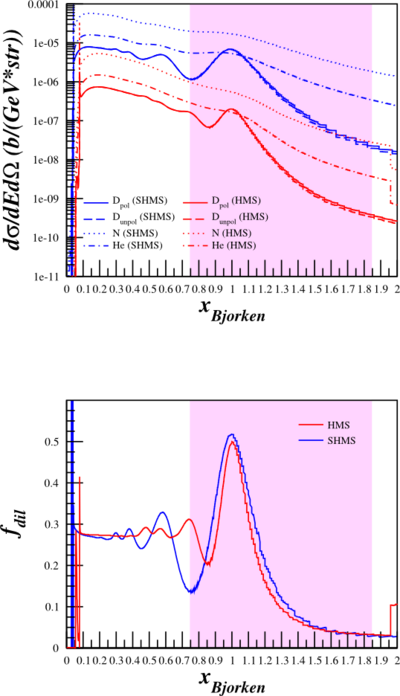
6.6 GeV Optimization Results
| <math>E_{\mathrm{beam}}=6.6\mathrm{~GeV}</math>
|
<math>\mathrm{HMS~}\theta_{e'}=12.382^{\circ}</math>
<math>\mathrm{HMS~}E'=5.862\mathrm{~GeV}</math>
<math>\mathrm{HMS~}Q^2=1.800\mathrm{~(GeV/}c)^2</math>
|
<math>\mathrm{SHMS~}\theta_{e'}=8.231^{\circ}</math>
<math>\mathrm{SHMS~}E'=6.252\mathrm{~GeV}</math>
<math>\mathrm{SHMS~}Q^2=0.850\mathrm{~(GeV/}c)^2</math>
|
|
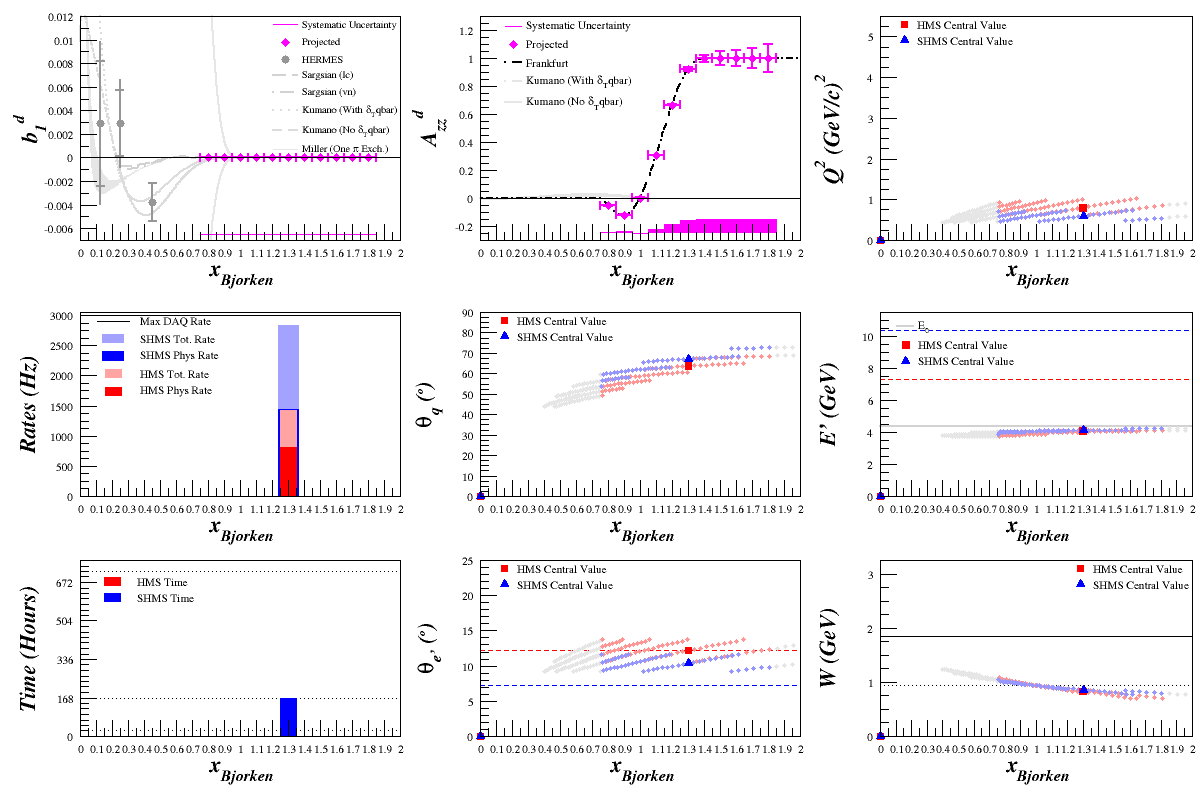
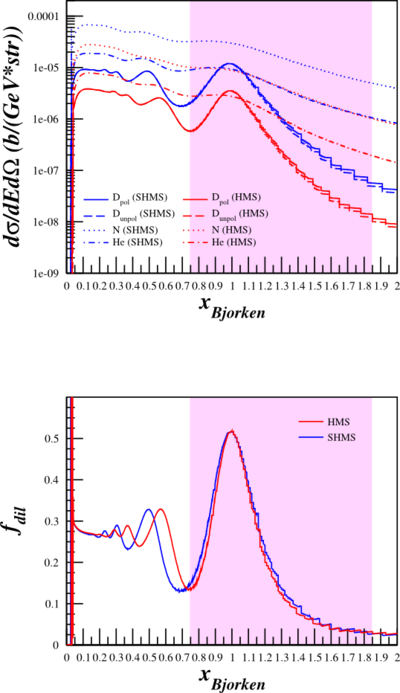
4.4 GeV Optimization Results
| <math>E_{\mathrm{beam}}=4.4\mathrm{~GeV}</math>
|
<math>\mathrm{HMS~}\theta_{e'}=12.212^{\circ}</math>
<math>\mathrm{HMS~}E'=4.068\mathrm{~GeV}</math>
<math>\mathrm{HMS~}Q^2=0.810\mathrm{~(GeV/}c)^2</math>
|
<math>\mathrm{SHMS~}\theta_{e'}=10.395^{\circ}</math>
<math>\mathrm{SHMS~}E'=4.154\mathrm{~GeV}</math>
<math>\mathrm{SHMS~}Q^2=0.600\mathrm{~(GeV/}c)^2</math>
|
|
2.2 GeV Optimization Results
| <math>E_{\mathrm{beam}}=2.2\mathrm{~GeV}</math>
|
<math>\mathrm{HMS~}\theta_{e'}=16.474^{\circ}</math>
<math>\mathrm{HMS~}E'=2.048\mathrm{~GeV}</math>
<math>\mathrm{HMS~}Q^2=0.370\mathrm{~(GeV/}c)^2</math>
|
<math>\mathrm{SHMS~}\theta_{e'}=15.490^{\circ}</math>
<math>\mathrm{SHMS~}E'=2.065\mathrm{~GeV}</math>
<math>\mathrm{SHMS~}Q^2=0.330\mathrm{~(GeV/}c)^2</math>
|
|
| Note: The HMS rates are higher than the SHMS rates, but the cross-sections show the opposite. I believe this is due to three more points on the HMS acceptance adding a small (three points) of phi-accentance that the SHMS doesn't have (see top-left HMS points in <math>\theta_{e'}</math> plot)
|
--E. Long 18:11, 8 October 2013 (UTC)





