Elong-15-04-07
Open Question
Can we measure t20 using inclusive D(e,e')? Or does it require a second spectrometer for exclusive D(e,e'D)? I can't find a single past measurement of t20 done using inclusive scattering, although the formalism seems to be nearly identical to our D(e,e') Azz measurements. Or does adding our dilution factor (since we're not tagging deuterons) fix the discrepancy?
Relating t20 and Azz
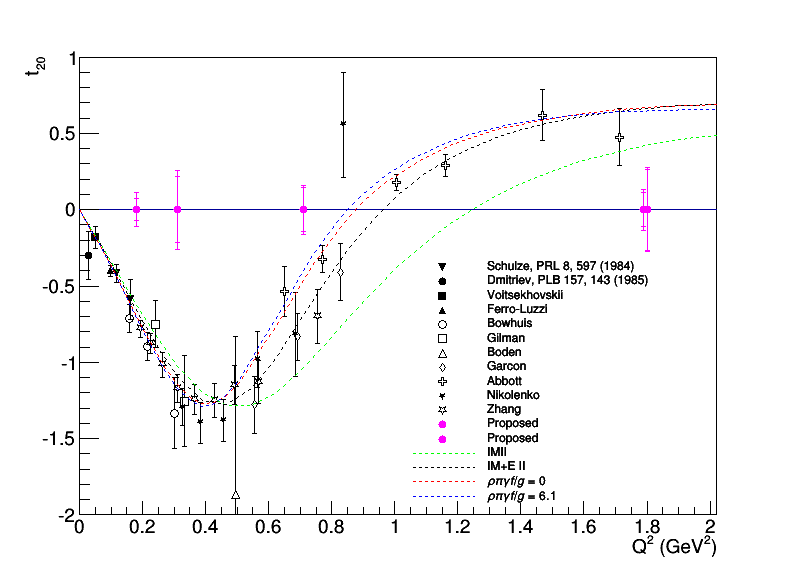
The Boden '91 paper, the only existing t20 measurement taken with a solid ND3 target, does a nice job of describing the relationship between the measured ratio and t20. Eq. 1 describes their ratio,
<math>R_{exp}=\frac{d\sigma_p}{d\sigma_u}=1+P_{zz} \left( \frac{d\sigma_T-d\sigma_u}{d\sigma_u} \right) = 1+P_{zz} \left( R_T-1 \right) </math>
<math>R_T-1 = \frac{1}{P_{zz}} \left( \frac{d\sigma_p}{d\sigma_u} -1 \right).</math>
This matches closely to our Azz,
<math>A_{zz}=\frac{2}{fP_{zz}}\left( \frac{d\sigma_p}{d\sigma_u}-1\right), </math>
where the <math>f=1</math> in the Boden result, since they are tagging deuterons and have negligible contamination.
The two are related by
<math>R_T-1=\frac{1}{2}A_{zz}.</math>
Later on in the paper, <math>(R_T-1)</math> is related to t20 by neglecting the (small) magnetic contributions to get
<math>t_{20}=-\sqrt{8}(R_T-1),</math>
which we can relate to our Azz above by
<math>t_{20}=-\sqrt{2}A_{zz}.</math>
Adjusting the uncertainties calculated last week, which were simply Azz at x=2, by
<math>\delta t_{20} = \sqrt{2}\delta A_{zz},</math>
we get the plot below.
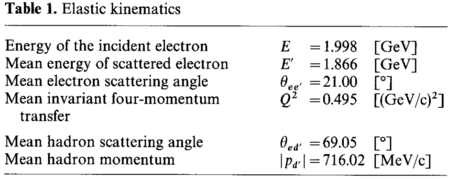
An important caveat related to the first topic above: The Boden measurement tags deuterons with a hadron scattering angle of ~70 deg, which is where each t20 measurement was taken or rotated to on the plot above.