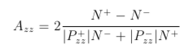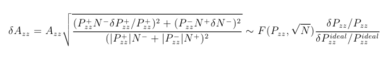Final Look

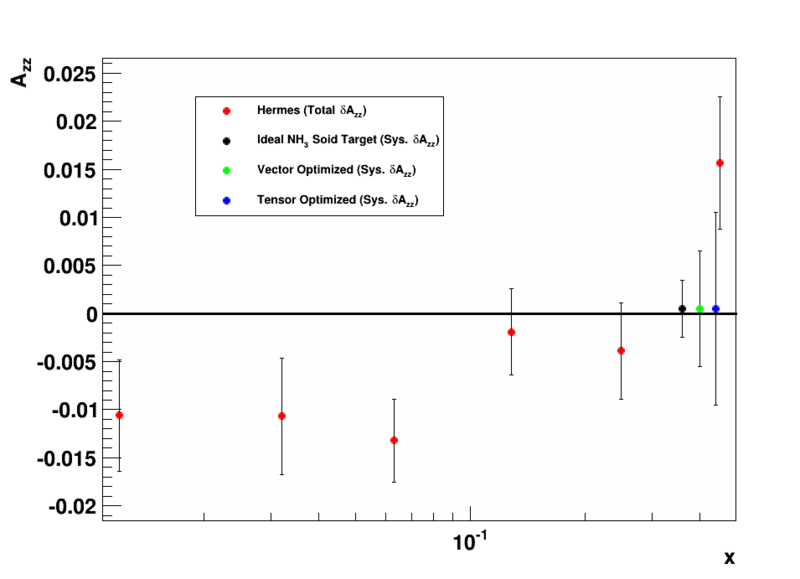
Error estimate based on previous analysis using standard solid polarized targets results indicated in first write-up based on an asymmetry A_zz

with an absolute systematic uncertainty estimated from,

To obtain tensor polarization by optimizing vector polarization we expect a tensor polarization of P_zz=2-(4-3P²)^1/2 assuming a Boltzman distribution at thermal equilibrium.

But not at thermal equilibrium under experiment (trying not to under estimate error)
Analytic relation not applicable for tensor Optimization (hole burning)

General limitations for all tensor polarized experiments to keep in mind:
1.) Ideal P_zz =2.5%-5%
2.) Vector Optimized P_zz =6.5%-12%
3.) Tensor Optimized P_zz =15%-25%
4.) Negative tensor polarization not yet achieved without hole burning (very unstable)

→ Best Estimates for Cumulative Absolute Uncertainty
(No estimate from background or small coherent length nuclear effects)

What about other observables?

Still lots of experimental possibilities with tensor polarization:
1.) Cross section or Asymmetry (A_xx) based on positive Vector Optimized only
2.) Electrodisintegration
3.) Photodisintegration
4.) CLAS photoproduction

Need to figure out what is interesting theoretically and not yet done...