Elong-13-04-29
Rates Update
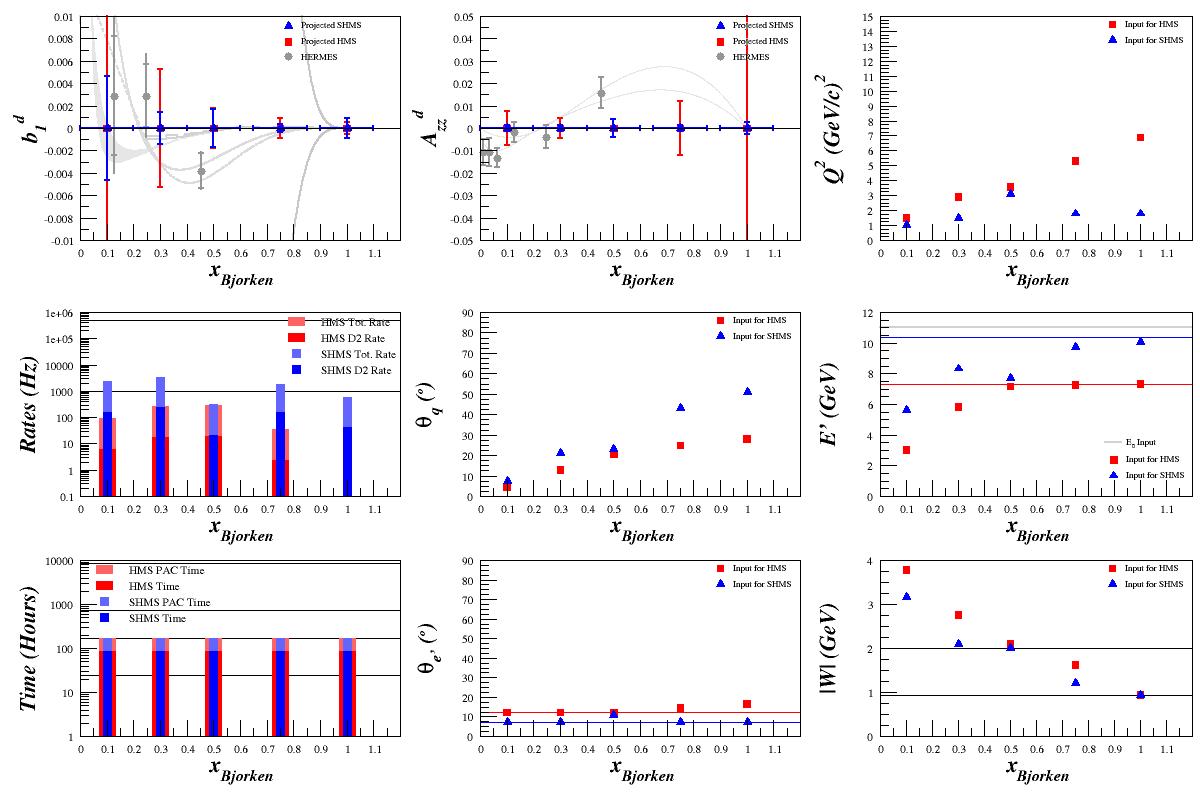
→ For the plots below, I assume the following:
Target Material ND3 Target Length 3 cm fdil (See below) pf 0.65 Pzz 20% E0 11 GeV xBjorken 0.1, 0.3, 0.5, 0.75, 1.0 Q2 Variable θq Calculated θe' Calculated E' Calculated W Calculated
- → θe' and E' limits were added for each spectrometer
- → Error bars shown are statistical only
- → F1 and F2 are calculated using the Bosted fits, which lets us extend into a higher <x> range
- → It is valid for 0<W<3.2 GeV and 0.2<Q2<5 GeV2
- → The error bars are calculated from:
- $dA_{zz} = \left( \frac{4}{f_{\mathrm{dil}}N_DP_{zz}} \right) \cdot \left( \frac{1}{\sqrt{t\cdot R_D}} \right)$
- $db_1^d = |1.5\cdot dA_{zz}| \cdot F_1^d$
Dilution Factor
I've been a bit confused by the dilution factor, f. It stems from:
$f=\frac{N_{D}}{(N_{D}+N_{N}+N_{He})} = \frac{t\cdot R_{D}}{(t\cdot R_{D}+t\cdot R_{N}+t\cdot R_{He})} = \frac{R_{D}}{(R_{D}+R_{N}+R_{He})} \approx \frac{N_{D}}{N_{D}+N_{N}}\approx \frac{3\sigma_{D}}{3\sigma_{D}+\sigma{N}}\approx \frac{3\cdot 2}{3\cdot 2 + 14}\approx 6/20=0.3$, but I'm having difficulties matching that and the trouble seems to be coming from the cross-sections.
The cross section I'm using is
$\frac{d^2\sigma^u}{d\Omega dE'} = \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}} \left[ \frac{2\cdot F_1^{X}}{m_{X}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{F_2^X}{\nu} \right]$
where X = nucleus and $\left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}}=\frac{Z^2 A^2 \hbar^2 c^2}{4E^2\sin^4\left( \frac{\theta}{2} \right)}\cos^2\left( \frac{\theta}{2} \right)$.
Using the Bosted code, I get
| <x> | Q 2 | $F_1^X$ | $F_2^X$ | $\frac{d^2\sigma^u_X}{d\Omega dE'}$ | |
| D | 0.1 | 1.01 | 2.16 | 0.558 | $1.57 \cdot 10^{-7}$ |
| N | 0.1 | 1.01 | 14.8 | 3.99 | $9.40 \cdot 10^{-5}$ |
| D | 0.3 | 1.50 | 0.816 | 0.509 | $2.35 \cdot 10^{-7}$ |
| N | 0.3 | 1.50 | 5.72 | 3.73 | $1.75 \cdot 10^{-4}$ |
| D | 0.5 | 3.10 | 0.284 | 0.258 | $2.12 \cdot 10^{-8}$ |
| N | 0.5 | 3.10 | 1.95 | 1.79 | $1.35 \cdot 10^{-5}$ |
| D | 0.75 | 1.75 | 0.162 | 0.129 | $1.35 \cdot 10^{-7}$ |
| N | 0.75 | 1.75 | 0.765 | 0.632 | $6.40 \cdot 10^{-5}$ |
| D | 0.98 | 1.80 | 0.197 | 0.157 | $2.08 \cdot 10^{-7}$ |
| N | 0.98 | 1.80 | 0.190 | 0.322 | $4.13 \cdot 10^{-5}$ |
This, however, gives $f\approx 0.005$.
If, instead, I use $\frac{d^2\sigma^u}{d\Omega dE'} = \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}} \left( \frac{2F_1^X}{m_Xc^2} \right) \left[ \tan^2\left(\frac{\theta}{2}\right) +\frac{Q^2}{2\nu^2} \right]$, then I get
| <x> | Q 2 | $F_1^X$ | $F_2^X$ | $\frac{d^2\sigma^u_X}{d\Omega dE'}$ | |
| D | 0.1 | 1.01 | 2.16 | 0.558 | $1.27 \cdot 10^{-7}$ |
| N | 0.1 | 1.01 | 14.8 | 5.70 | $9.40 \cdot 10^{-6}$ |
| D | 0.3 | 1.50 | 0.816 | 0.509 | $2.44 \cdot 10^{-7}$ |
| N | 0.3 | 1.50 | 5.72 | 1.12 | $1.75 \cdot 10^{-5}$ |
| D | 0.5 | 3.10 | 0.284 | 0.258 | $2.32 \cdot 10^{-8}$ |
| N | 0.5 | 3.10 | 1.95 | 1.05 | $1.35 \cdot 10^{-6}$ |
| D | 0.75 | 1.75 | 0.162 | 0.129 | $2.53 \cdot 10^{-7}$ |
| N | 0.75 | 1.75 | 0.765 | 7.84 | $6.40 \cdot 10^{-6}$ |
| D | 0.98 | 1.80 | 0.197 | 0.157 | $5.08 \cdot 10^{-7}$ |
| N | 0.98 | 1.80 | 0.190 | 0.322 | $3.21 \cdot 10^{-6}$ |
with $f \approx 0.062$ for <x>=0.1, 0.3, and 0.5, $f \approx 0.088$ for <x>=0.75, and $f \approx 0.32$ for <x>=0.98.
The above are for specific cross-checks. If I take input the second method into the code, which scans cross-sections only within the range that the SMHS can accept, and finding $f = \frac{R_D}{R_D + R_N + R_{He}}$ then we get $f \approx 0.065 - 0.080$ and the following statistics:
Maximizing Rate (Minimizing dAzz)
Using $\frac{d^2\sigma^u}{d\Omega dE'} = \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}} \left[ \frac{2\cdot F_1^{X}}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{F_2^X}{\nu} \right]$
If we set the spectrometer such that we aim to increase the rate as high as we can, it will get us the lowest (statistically) achievable Azz.
<x> dAzz with SHMS dAzz with HMS db1 with SHMS db1 with HMS 0.1 0.00619 0.0316 0.0200 0.0770 0.3 0.00564 0.0203 0.00691 0.0244 0.5 0.0192 0.0204 0.00819 0.00853 0.75 0.00765 0.0593 0.00187 0.00444 1.0 0.0136 0.699 0.00421 0.00279
The db1 Problem
→ Since db1 is calculated from $db_1^d = |1.5\cdot dA_{zz}| \cdot F_1^d$, it is dependent upon F1
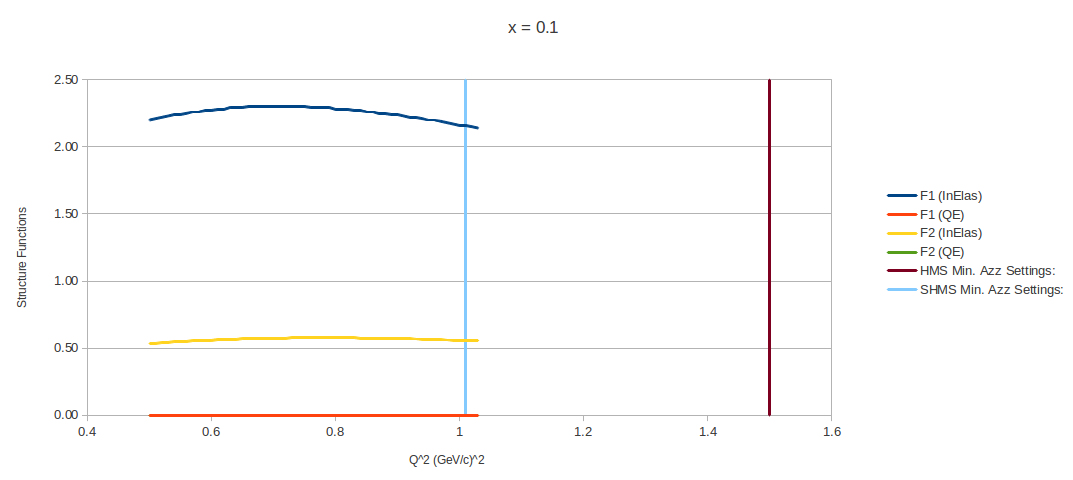
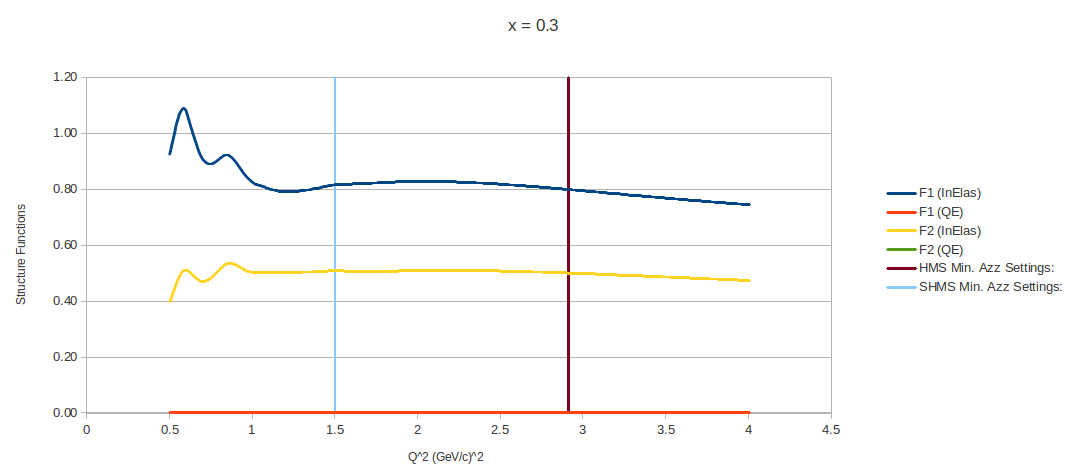
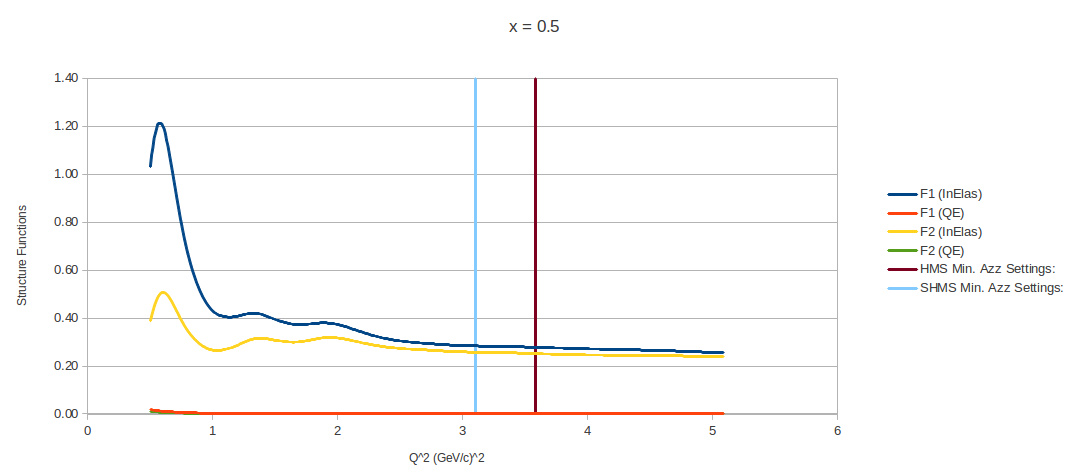
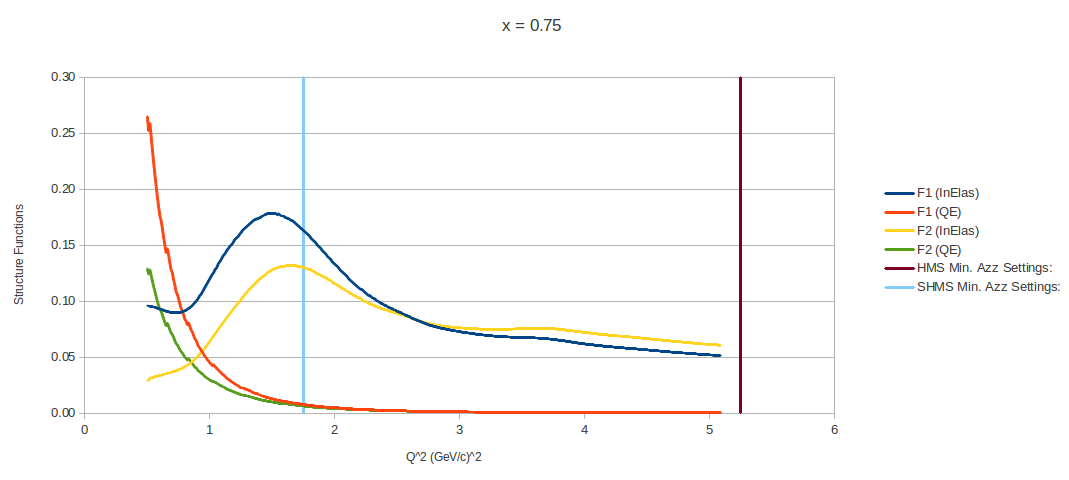
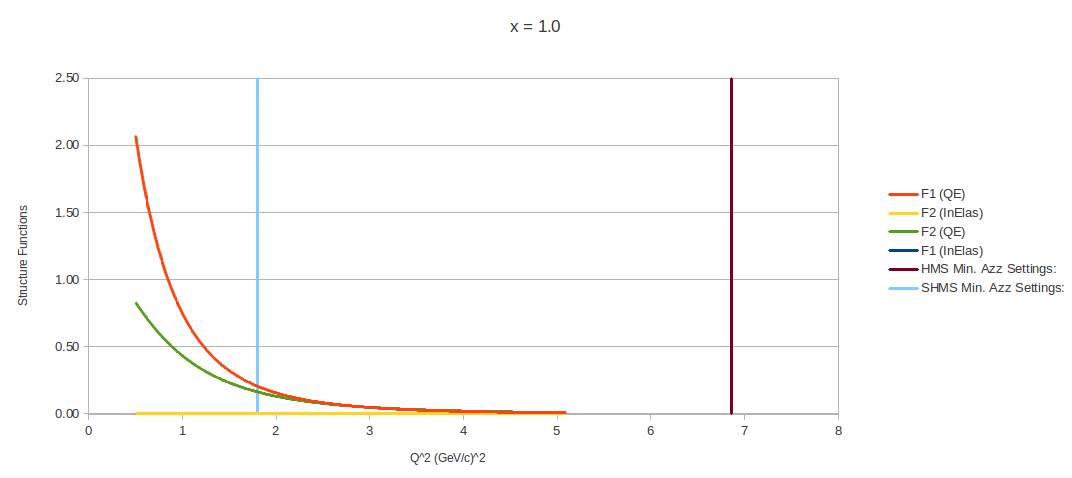
→ For each of the <x> values that I've been looking at, the following show what the Bosted code produces as a function of Structure Function vs. Q^2
→ For the plots below, the structure functions are calculated within the allowable Q 2 and W2 ranges of the Bosted fits
→ The two vertical lines indicate the Q 2 values where dAzz has been minimized
Minimizing db1
Using $\frac{d^2\sigma^u}{d\Omega dE'} = \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}} \left[ \frac{2\cdot F_1^{X}}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{F_2^X}{\nu} \right]$
If we set the spectrometer at the lowest allowed values of F1 (from above), it will get us the lowest (statistically) achievable db1.
<x> dAzz with SHMS dAzz with HMS db1 with SHMS db1 with HMS 0.1 0.00656 0.0316 0.0211 0.0770 0.3 0.0140 0.0203 0.0171 0.0244 0.5 0.0183 0.0204 0.00779 0.00853 0.75 0.00765 0.0593 0.00187 0.00444 1.0 0.0596 0.699 0.00103 0.00279
F1 Scan
Using the Bosted fits and scanning over the <x> range 0.1<x<1.5, in increments of 0.001, we can see that F1 will drop as we go to higher Q 2. This should cause the error bars on bd1 to drop accordingly, since $db_1^d = |1.5\cdot dA_{zz}| \cdot F_1^d$
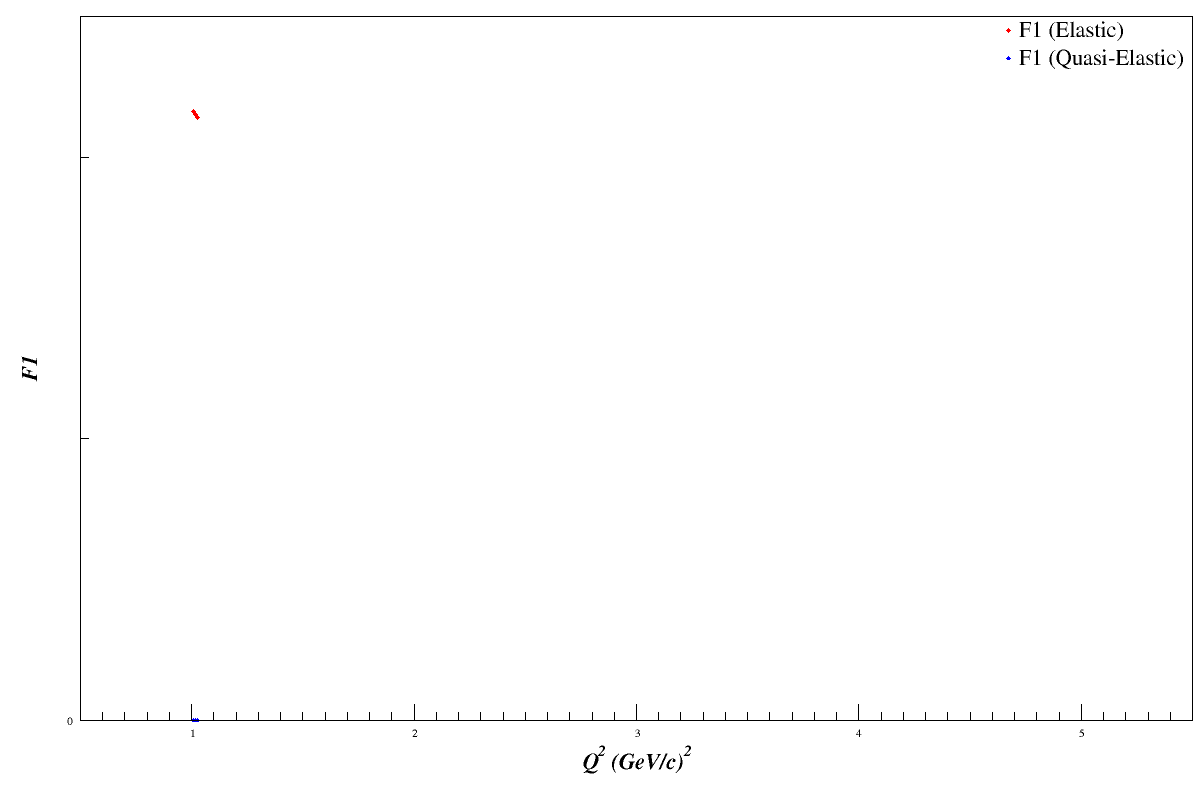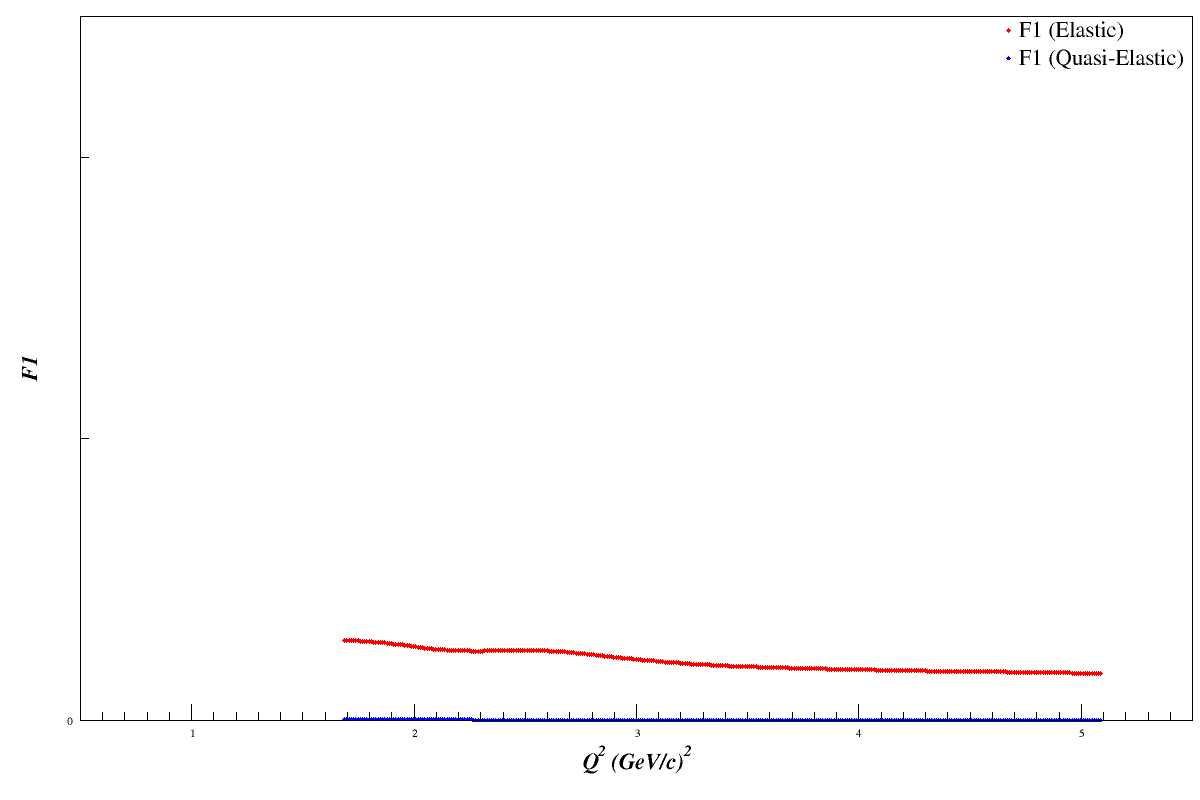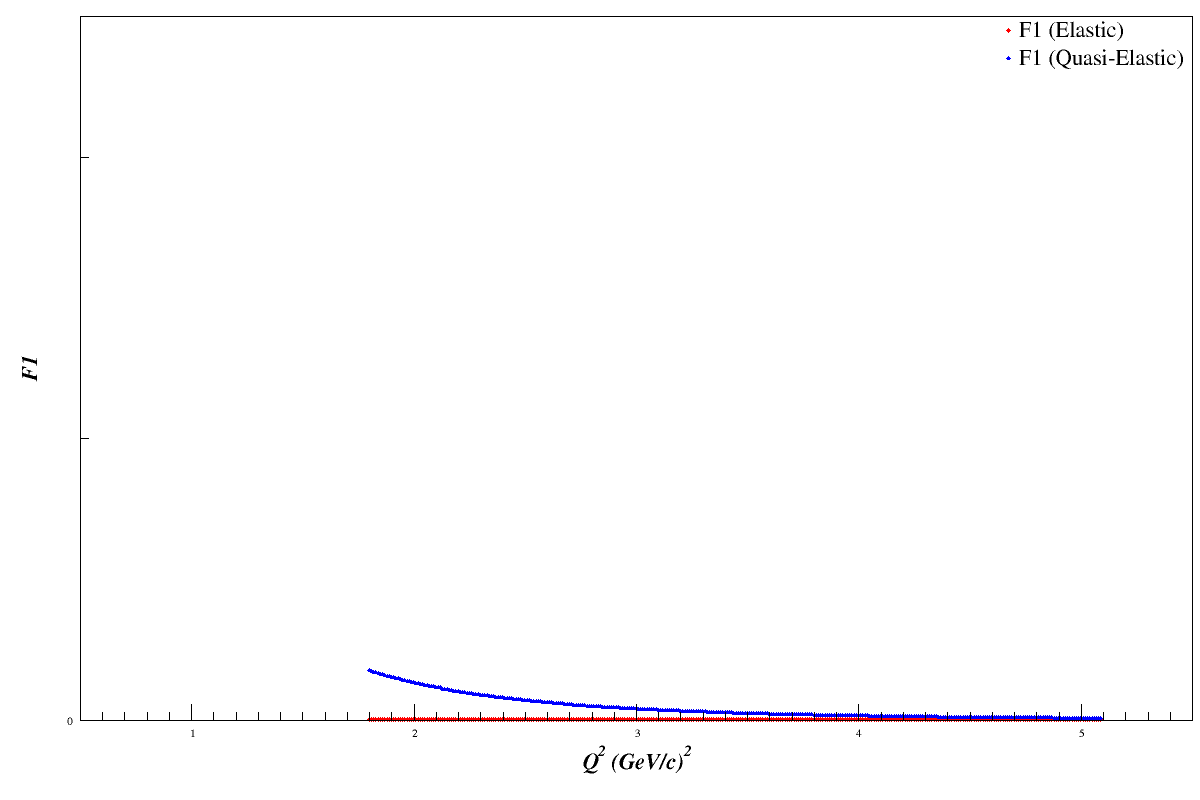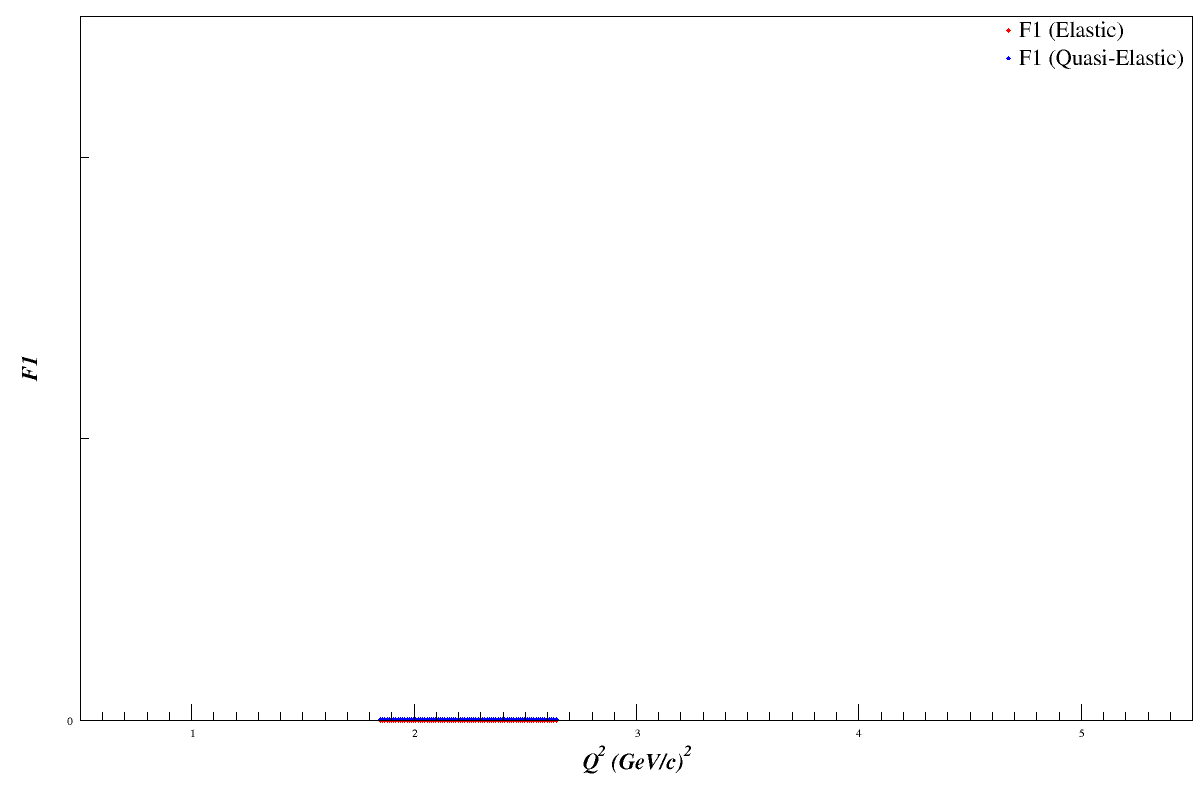
Summary
Using $\frac{d^2\sigma^u}{d\Omega dE'} = \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}} \left( \frac{2F_1^X}{m_Xc^2} \right) \left[ \tan^2\left(\frac{\theta}{2}\right) +\frac{Q^2}{2\nu^2} \right]$,
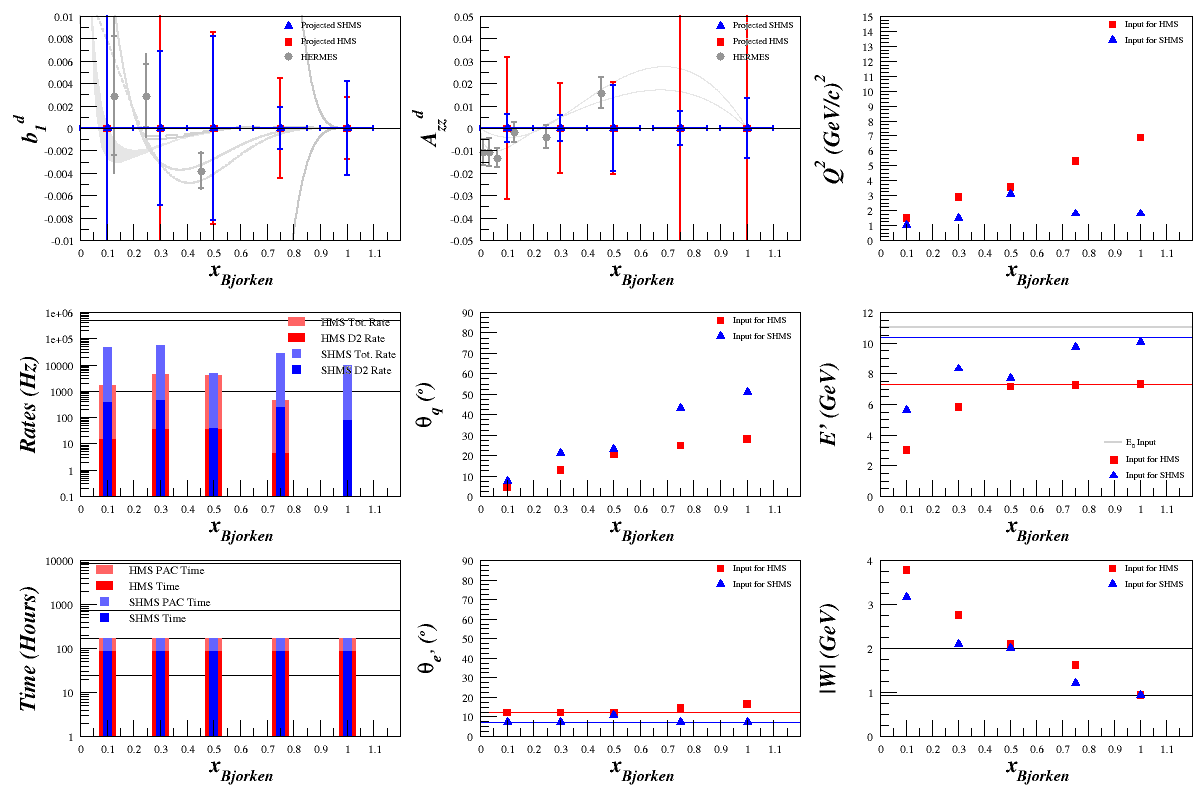
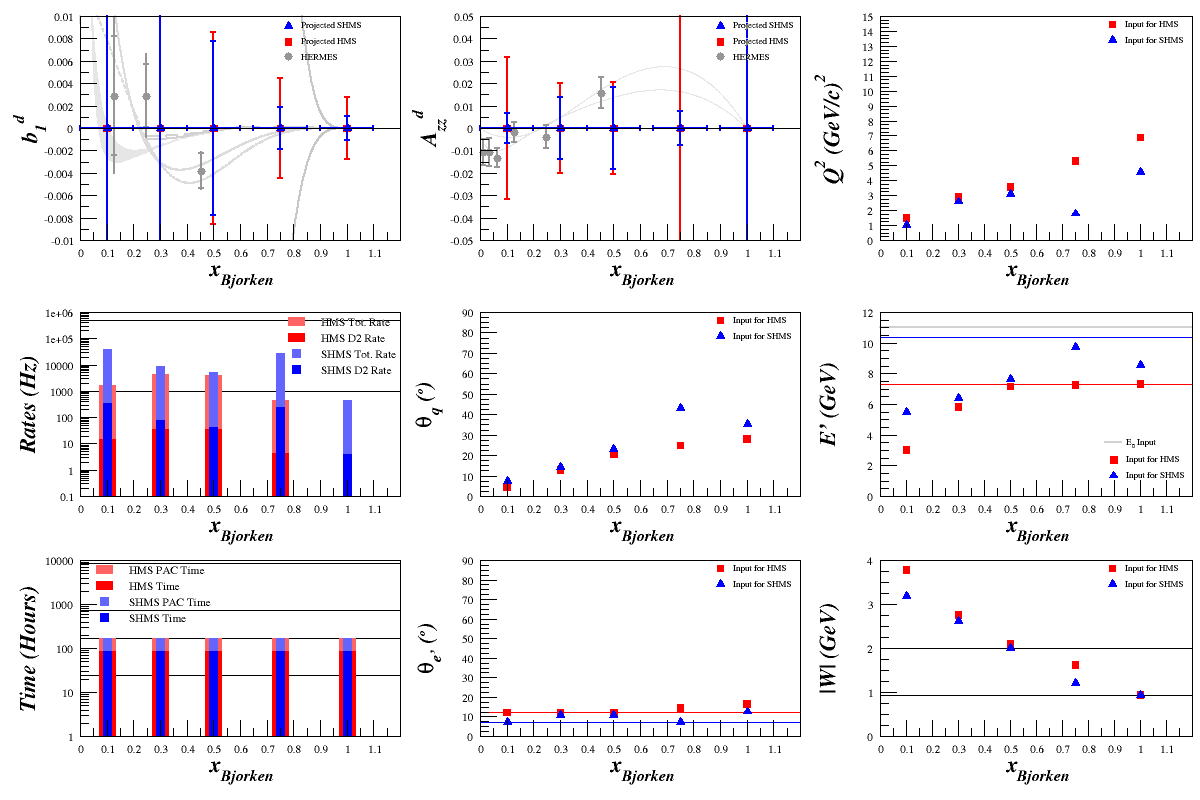
Some of the above still needs to be implemented, namely finding "sweet spots" in F1, but without that our statistics currently look like:
- → The error bars are calculated from:
- $dA_{zz} = \left( \frac{2}{f_{\mathrm{dil}}P_{zz}} \right) \cdot \left( \frac{1}{\sqrt{t\cdot R_{\mathrm{Total}}}} \right)$
- $db_1^d = |1.5\cdot dA_{zz}| \cdot F_1^d$
--E. Long 18:56, 29 April 2013 (UTC)