Elong-13-10-01
Cross Section Calculation
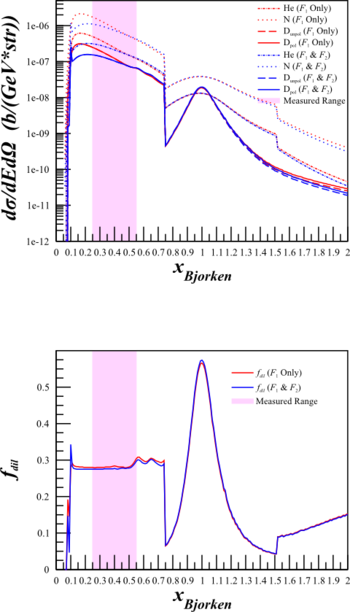
For previous calculations, I was using a simplified version of the cross-section where it was assumed that $F_2=2x\cdot F_1$, such that
$\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\right]\cdot \left[\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{Q^2 }{2\nu^2} \right] $.
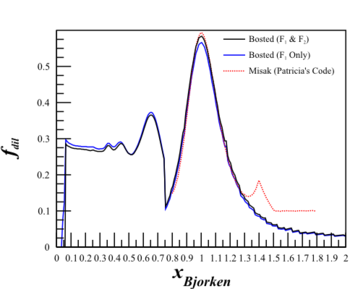
Since we're in a region that isn't DIS, I thought that the difference may be important so I incorporated $F_2$ from Bosted and removed the assumption:
$\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_1^{X}}{A_X} \right)}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_2^X}{A_X}\right) }{\nu} \right]$.
This increased the statistical uncertainty, particularly in the high-x region. It also lowered the rates dramatically, which gives us some room to play around with a lower $Q^2$.
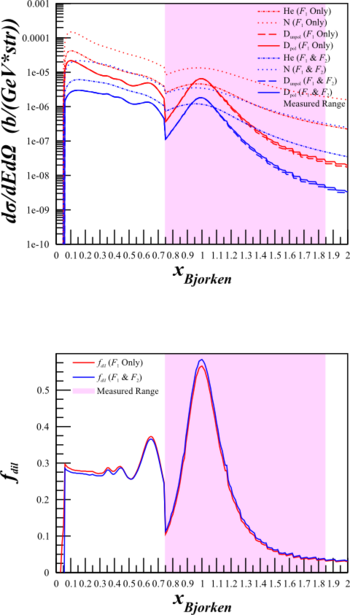
Although this changes the cross sections quite a bit,
| $F_1 \mathrm{~Only}$ | $F_1\mathrm{~and~}F_2$ |
|---|---|
 |
|
The dilution factor is nearly identical.
Cross Section Check for b1
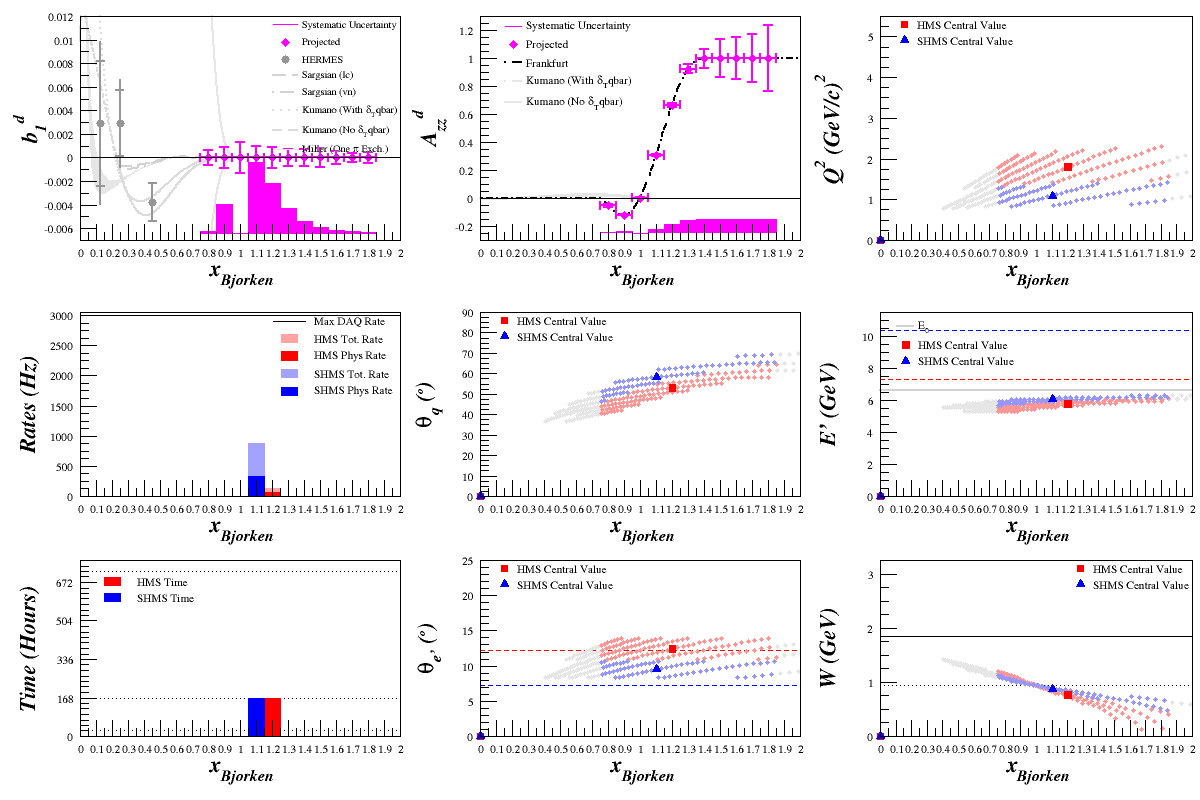
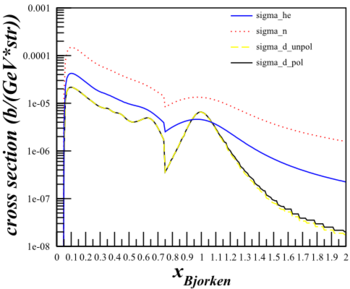
To see if this could cause a problem for the b1 statistics, I did a study of the effects of changing the cross section calculation from the simplified to the full for the b1 kinematics.
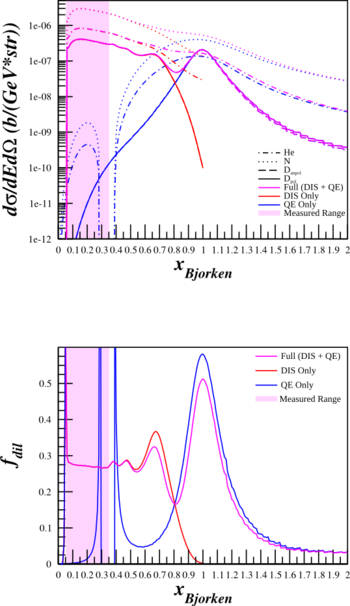
Cross Section Check for Azz
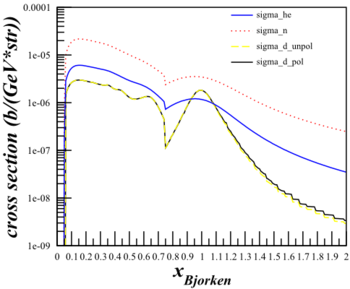
Same as the section above, looking at the difference between the simplified cross section using only $F_1$ and the full cross section using both $F_1$ and $F_2$, but for the Azz kinematics.
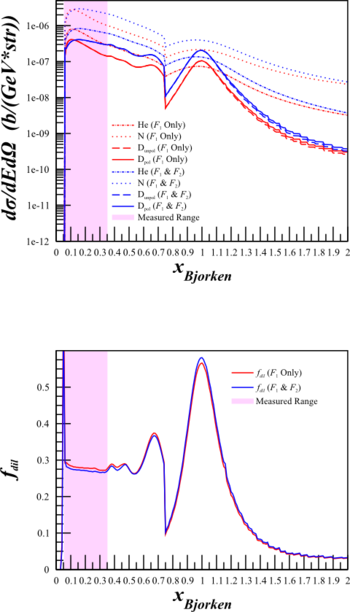
| HMS $\theta_{e'}=12.45^{\circ}$ $E'=5.80\mathrm{~GeV}$ |
SHMS $\theta_{e'}=9.51^{\circ}$ $E'=6.07\mathrm{~GeV}$ |
|---|---|
 |
|
Comparison to Data
In order to see how my calculations line up with actual data, I've taken the deuterium information from the quasi-elastic scattering archive data page to compare our cross section calculations for b1 and Azz. There are two measurements (both Shutz:1976) that are similar to our settings:
| Similar to $A_{zz}$ $E_{\mathrm{beam}}=6.519\mathrm{~GeV}$ $\theta_{e'}=8.00^{\circ}$ |
Similar to $b_1$ $E_{\mathrm{beam}}=11.671\mathrm{~GeV}$ $\theta_{e'}=8.00^{\circ}$ |
|---|---|
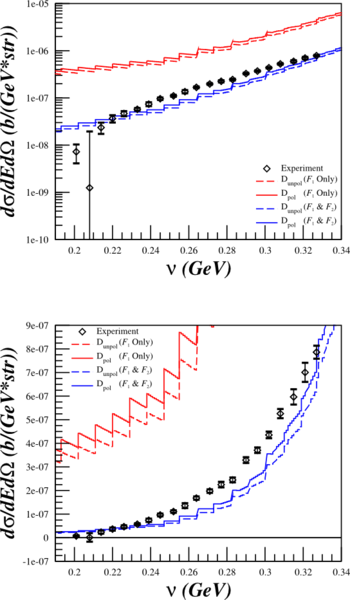 |

|
The top and bottom plots are the same, just that the top are on a log scale and the bottom on a linear scale.
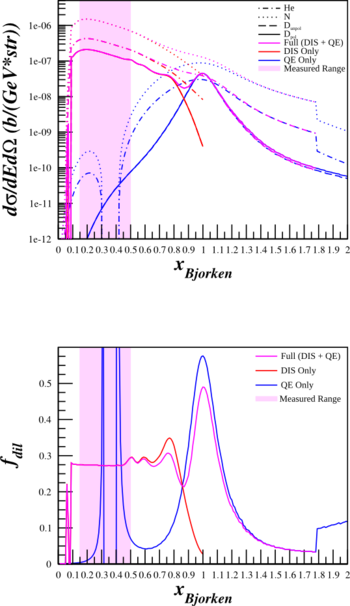
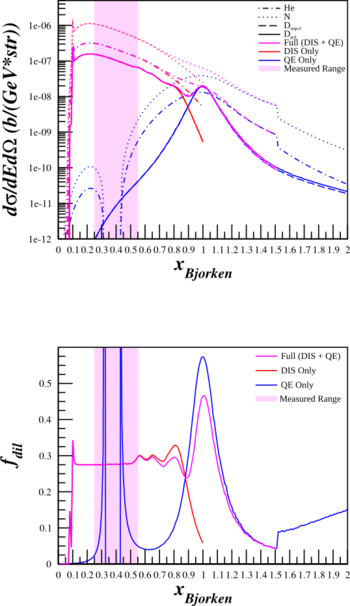
Inelastic and Quasielastic Structure Functions
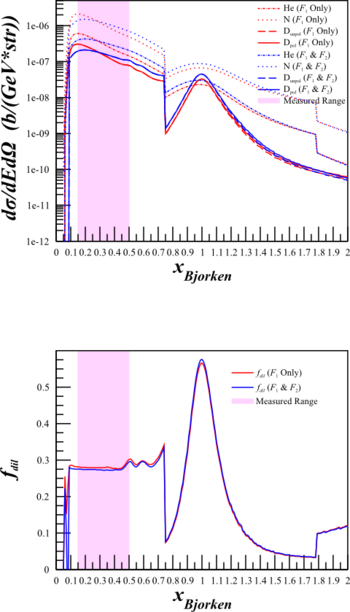
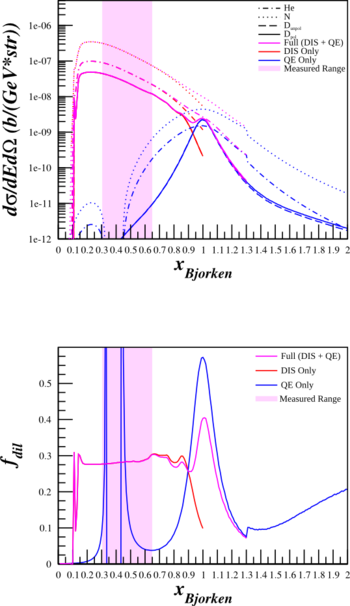
Previously, I've been shutting off the inelastic part of the structure functions and turning on the quasi-elastic when x=0.75. This creates a discontinuity and may cause trouble for estimating the dilution factor for Azz. As such, I've re-done the calculations of the cross sections and the dilution factors above using
$\frac{d^2\sigma^u}{d\Omega dE'} = A_X \left( \frac{d\sigma}{d\Omega} \right) _{\mathrm{Mott}_{\mathrm{p}}} \left[ \frac{2\cdot \left(\frac{F_{1IE}^X + F_{1QE}^X}{A_X} \right)}{m_{p}}\tan^2\left( \frac{\theta_{e'}}{2} \right) + \frac{\left( \frac{F_{2IE}^X+F_{2QE}^X}{A_X}\right) }{\nu} \right]$,
where $F_{1IE}^X$ and $F_{2IE}^X$ are the inelastic form factors, and $F_{1QE}^X$ and $F_{2QE}^X$ are the quasi-elastic form factors. Below are plots with the combined form factors (in purple) along with just the contribution from DIS (in red) and from QE (in blue).
| HMS $\theta_{e'}=12.45^{\circ}$ $E'=5.80\mathrm{~GeV}$ |
SHMS $\theta_{e'}=9.51^{\circ}$ $E'=6.07\mathrm{~GeV}$ |
|---|---|
 |

|
--E. Long 18:57, 2 October 2013 (UTC)