Elong-13-09-18
Optimizing Azz in QE and x>1 Range
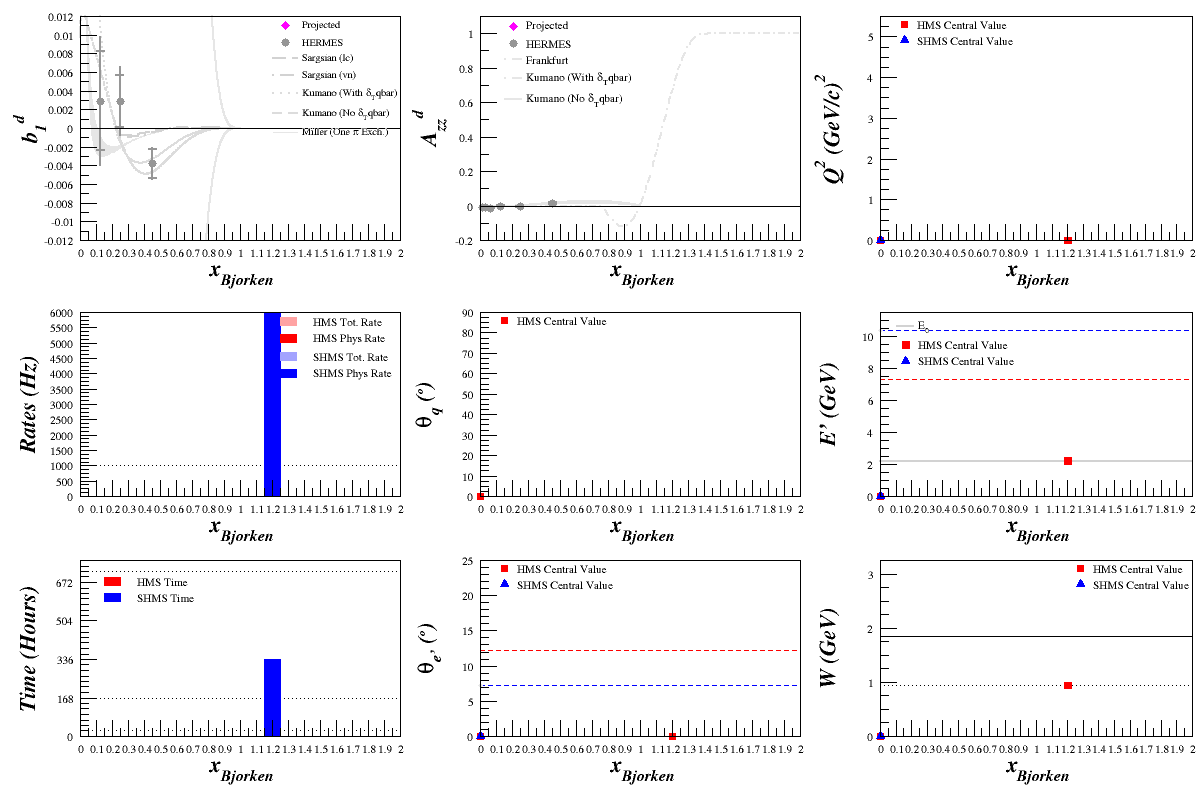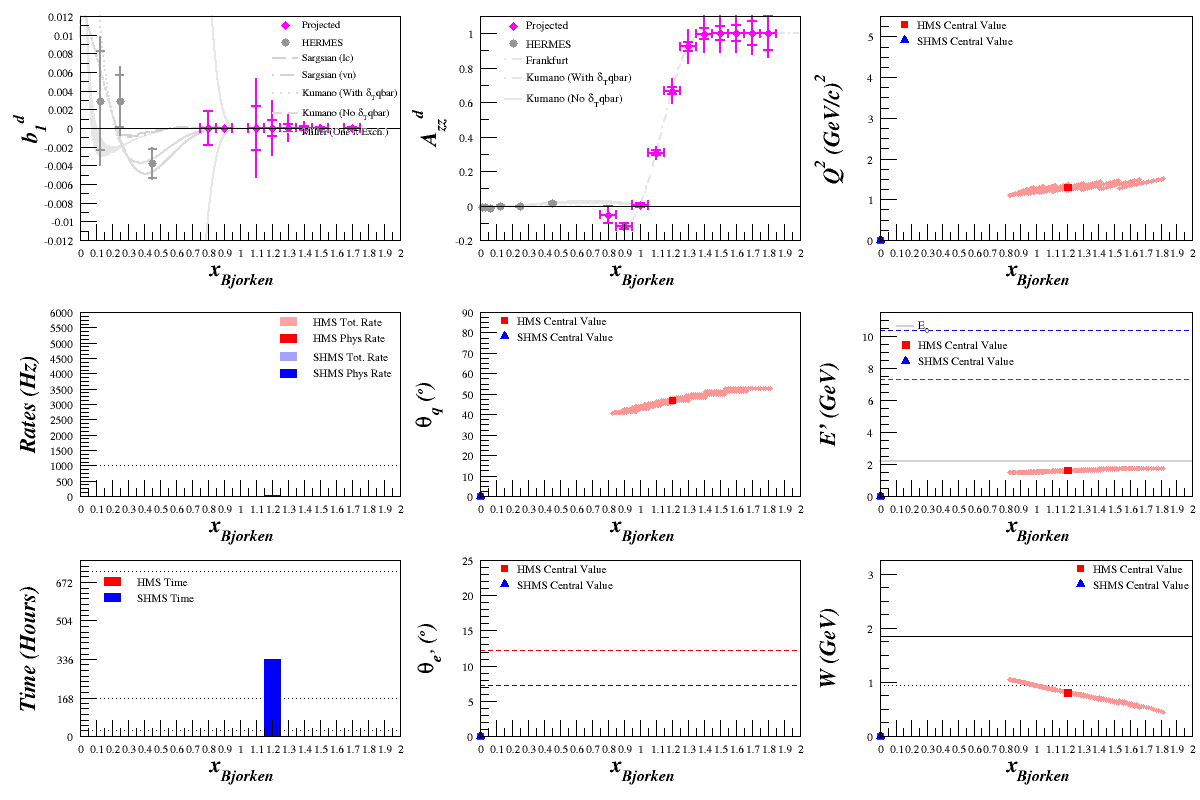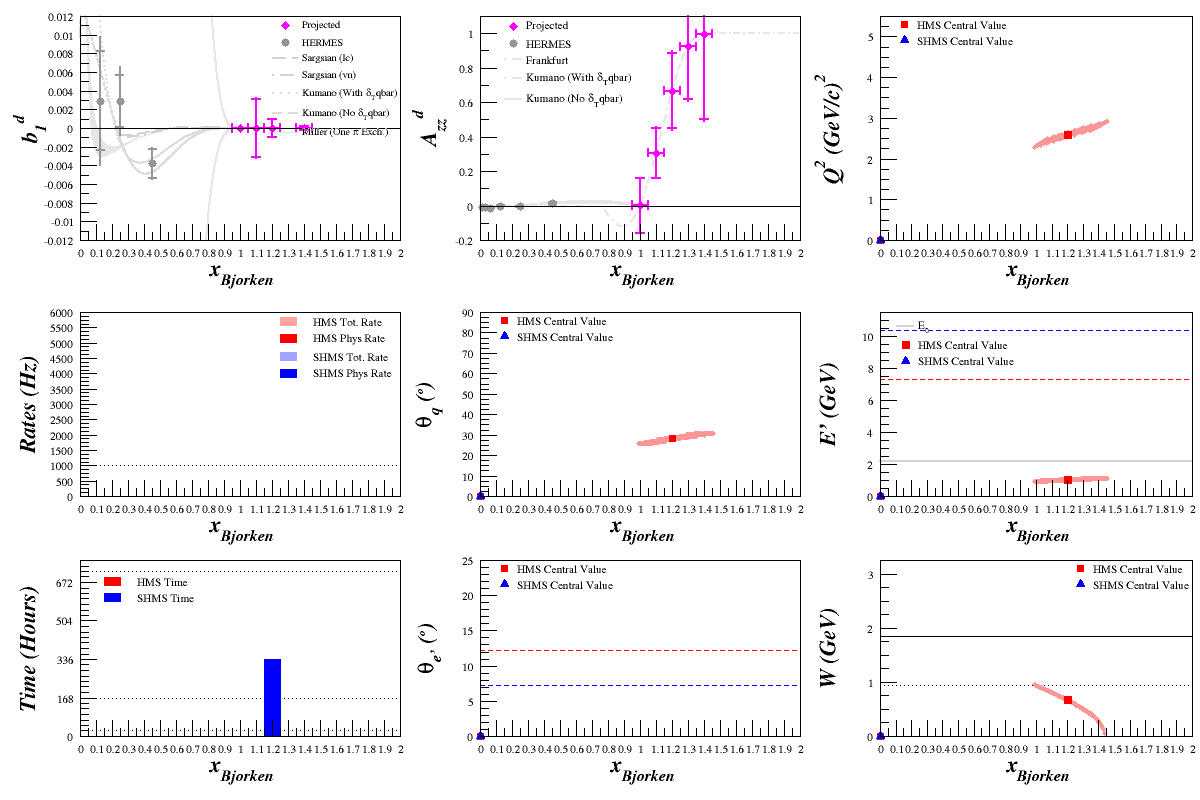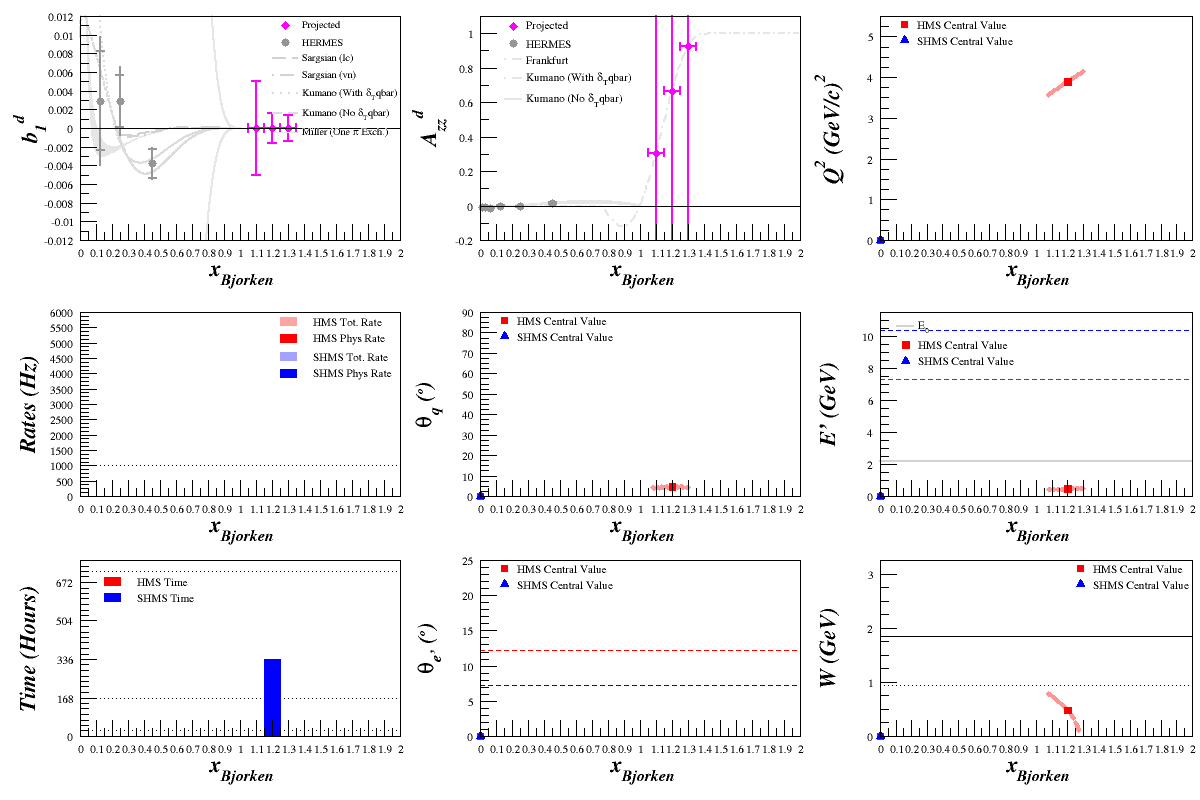
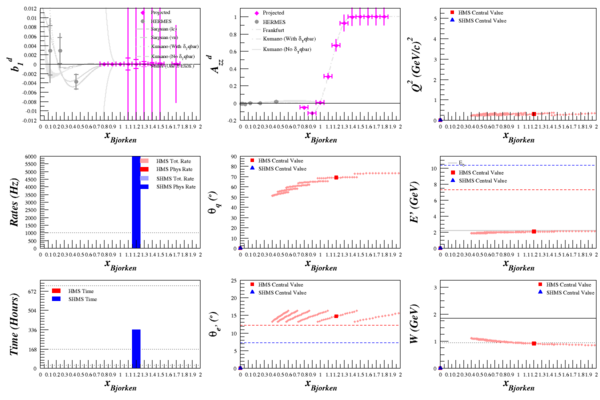
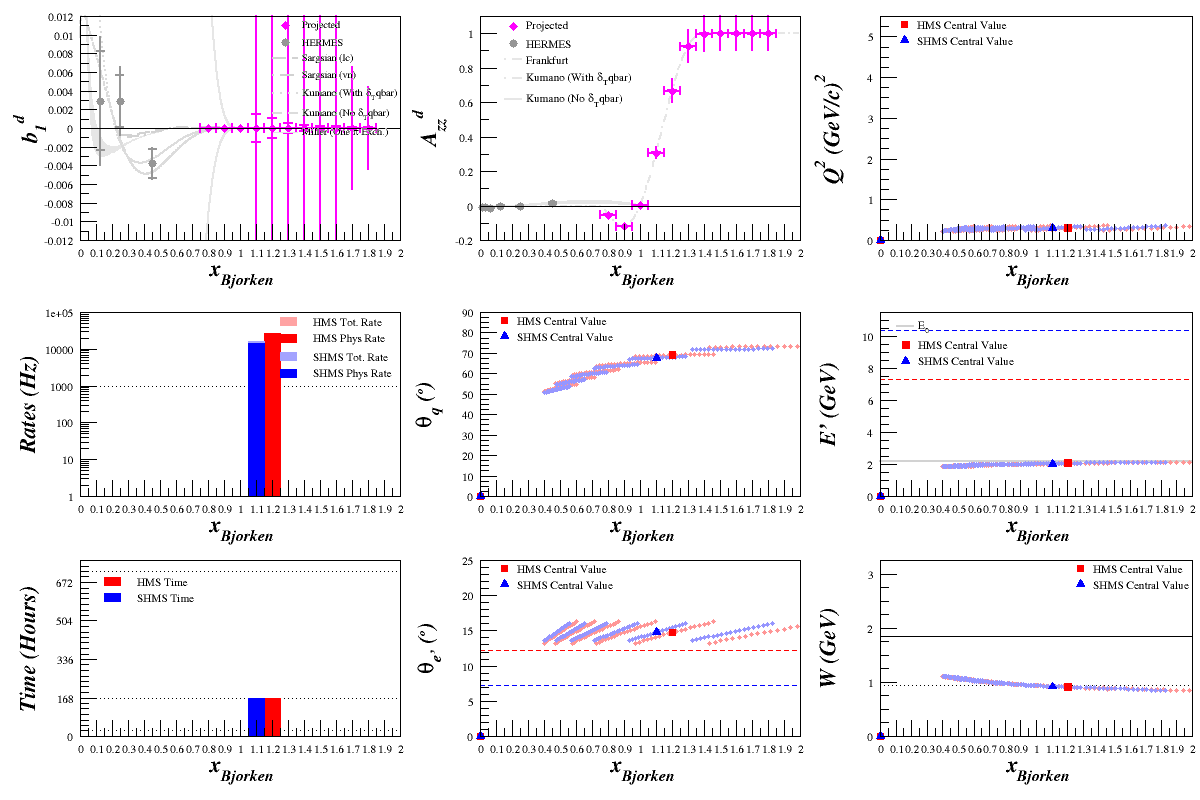
Beam Energy = 2.2 GeV
HMS
SHMS
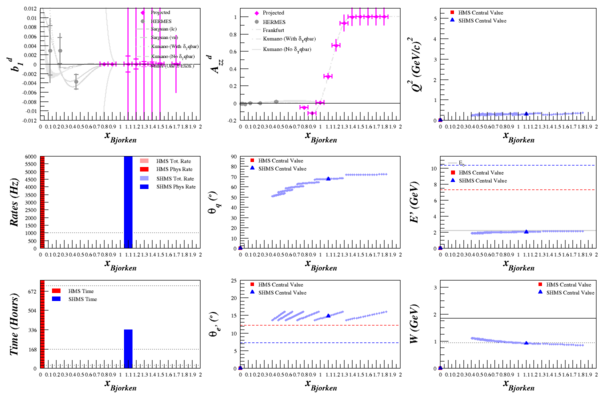
Beam Energy = 4.4 GeV
HMS
SHMS
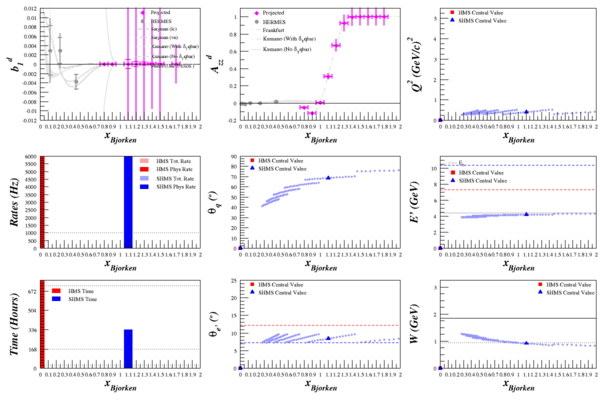
Beam Energy = 6.6 GeV
HMS
SHMS
Beam Energy = 8.8 GeV
HMS
SHMS
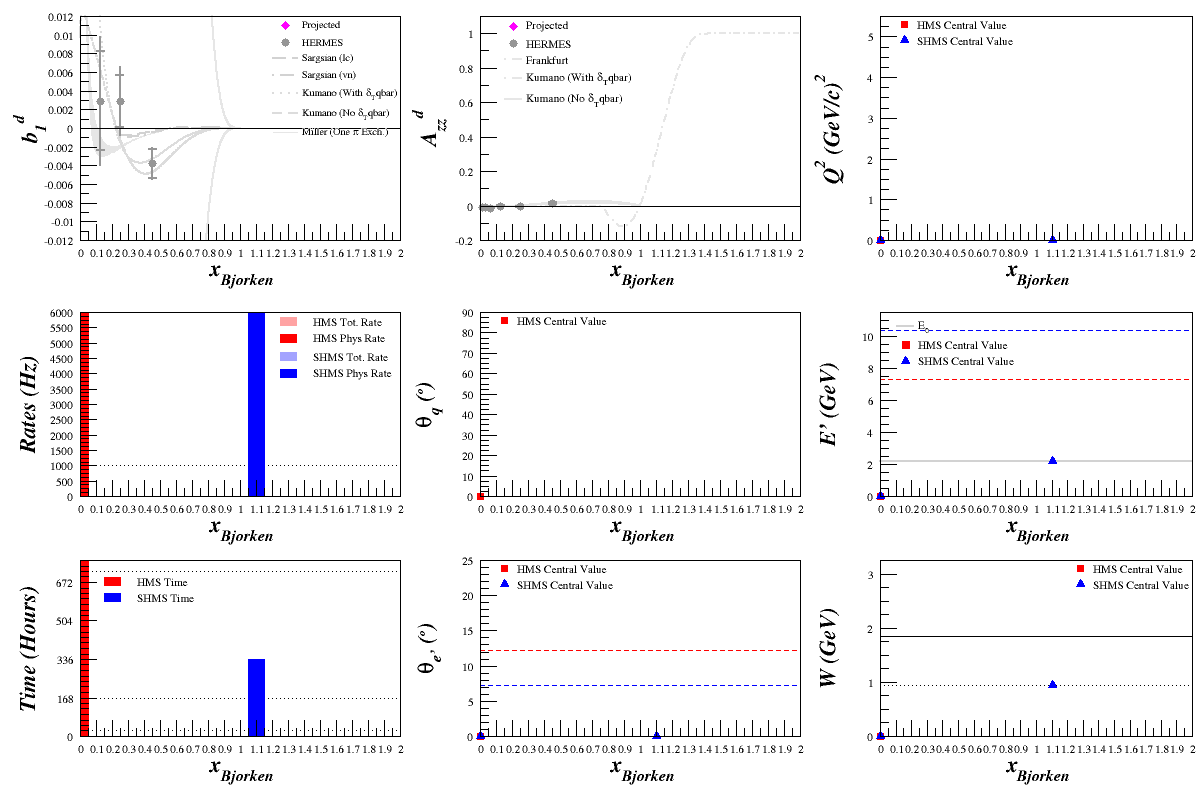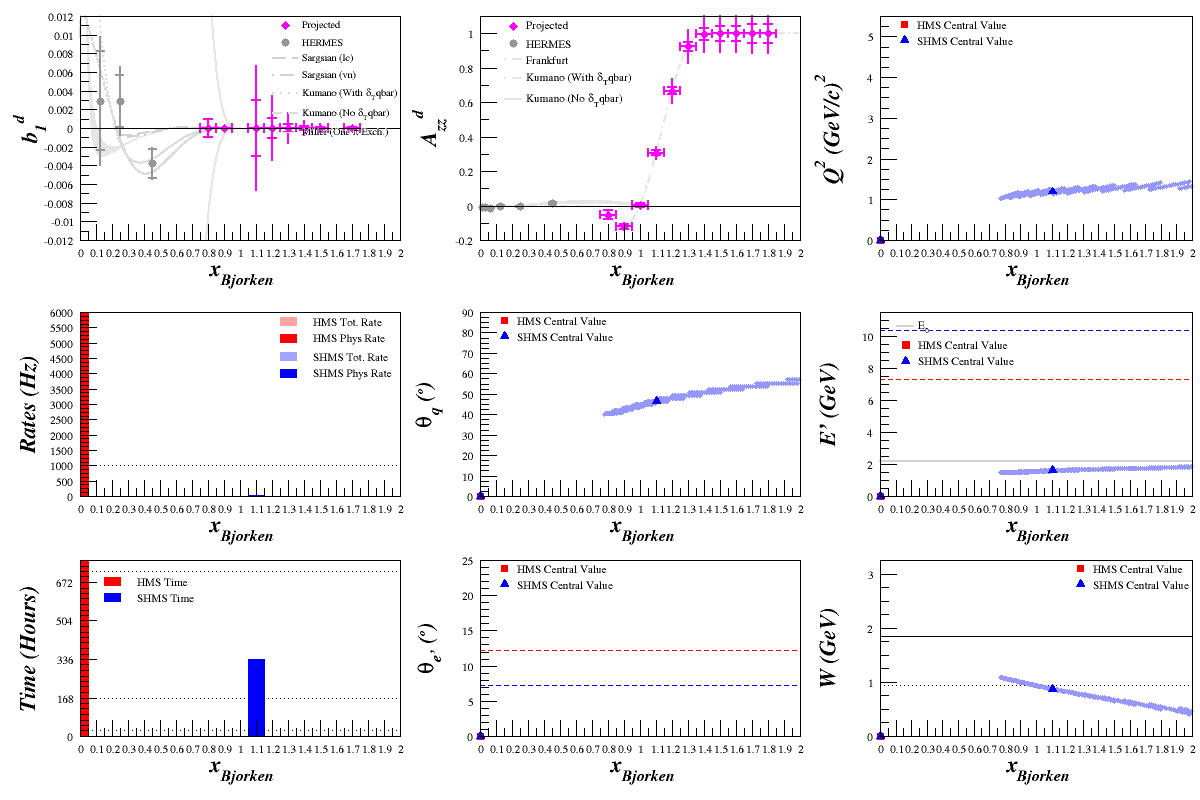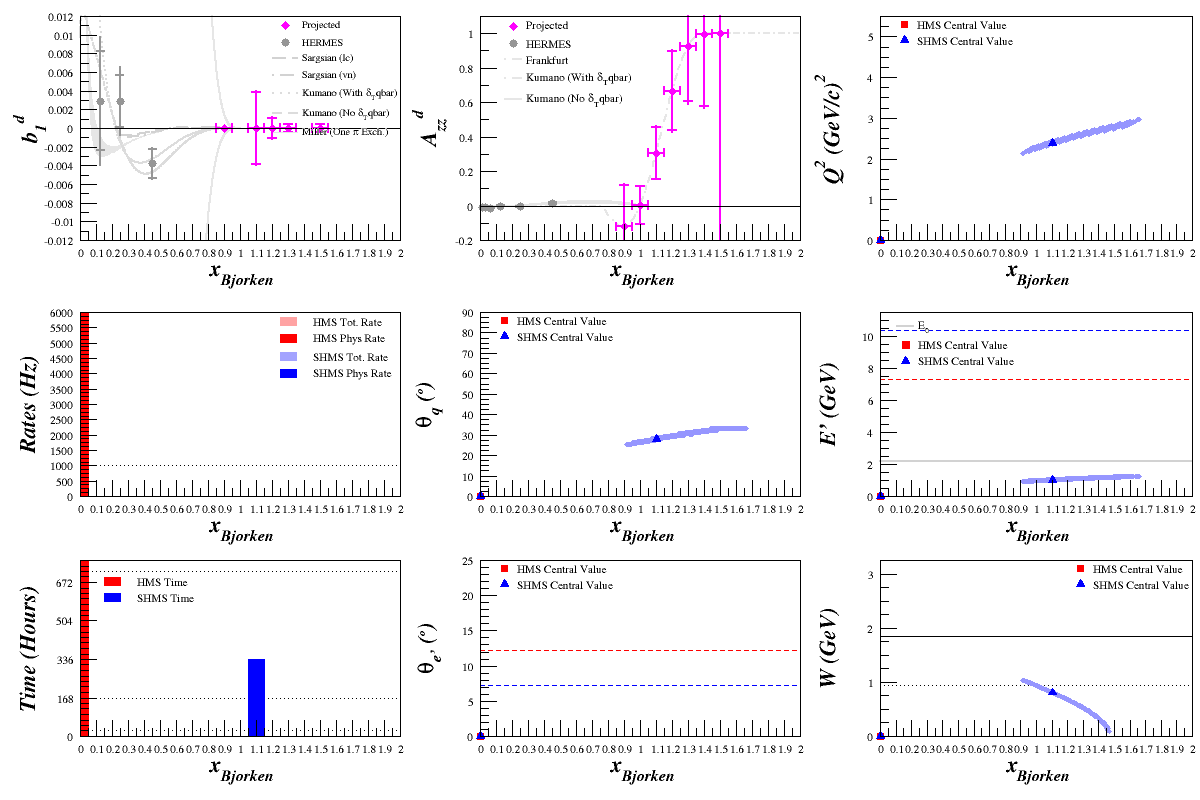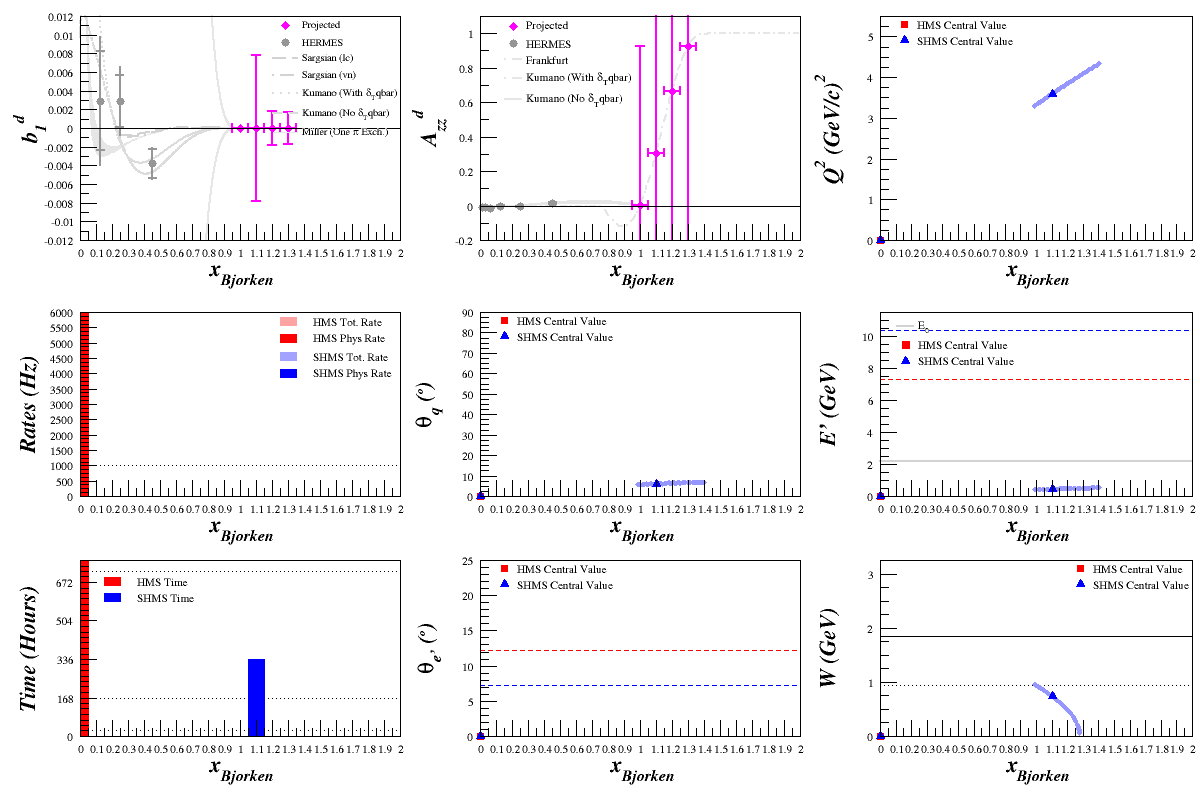
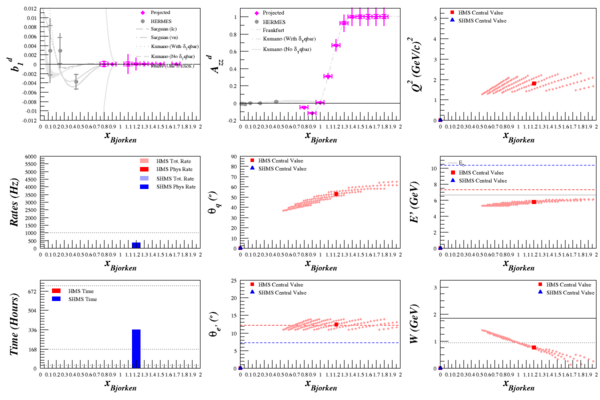
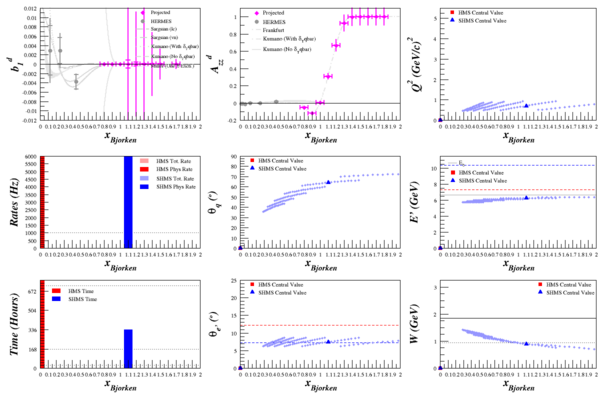
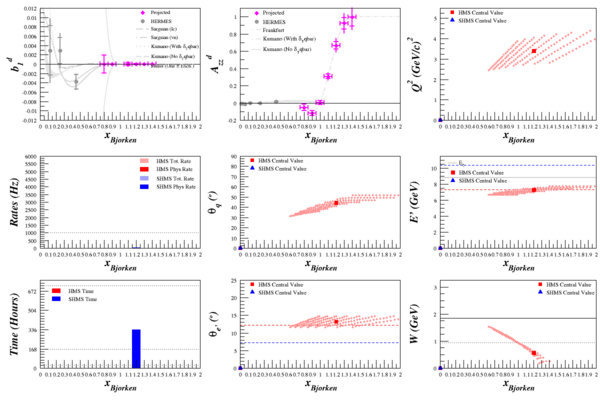
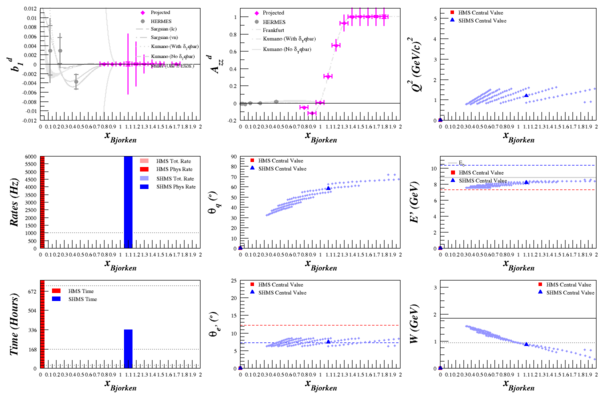
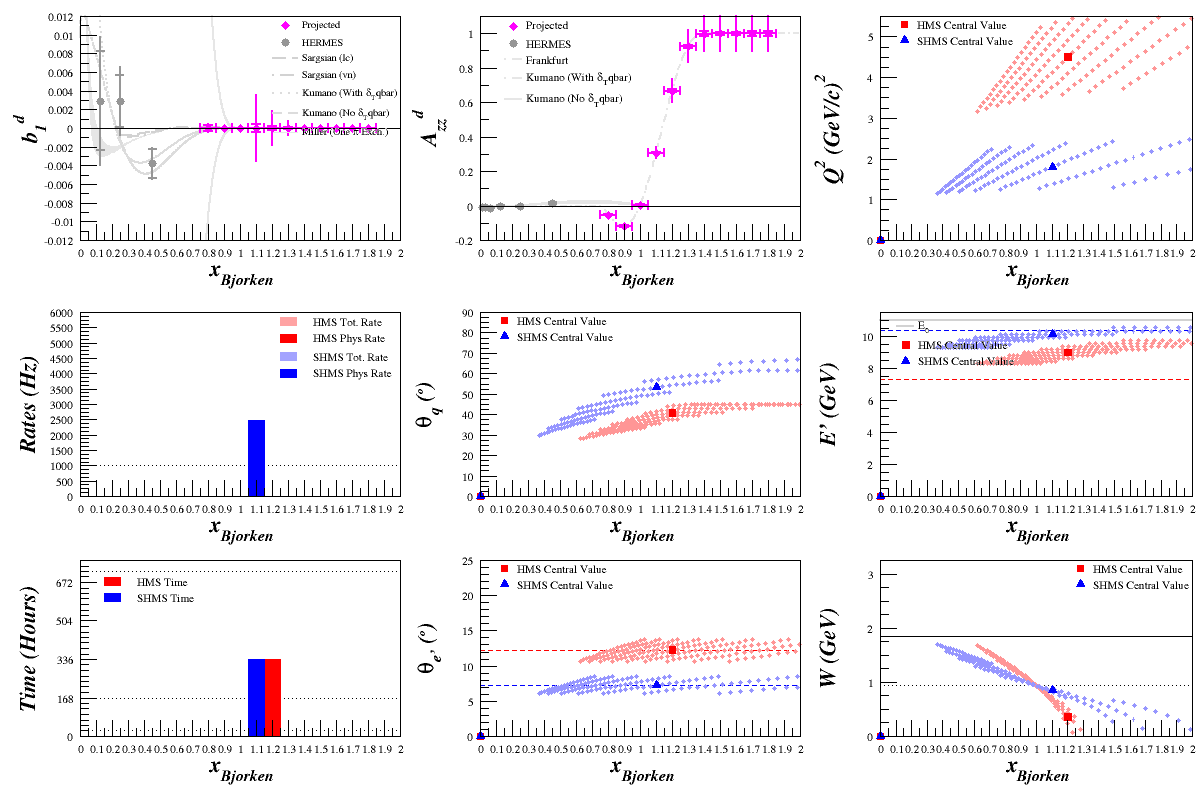
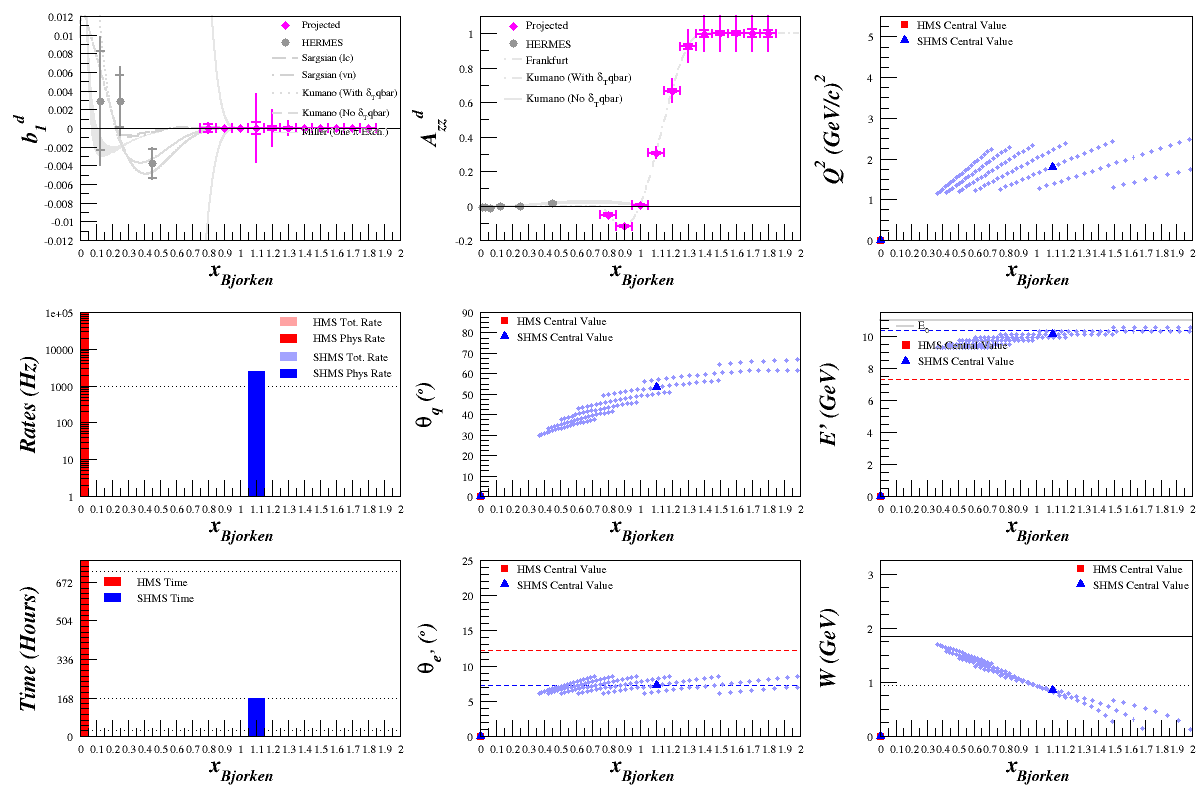
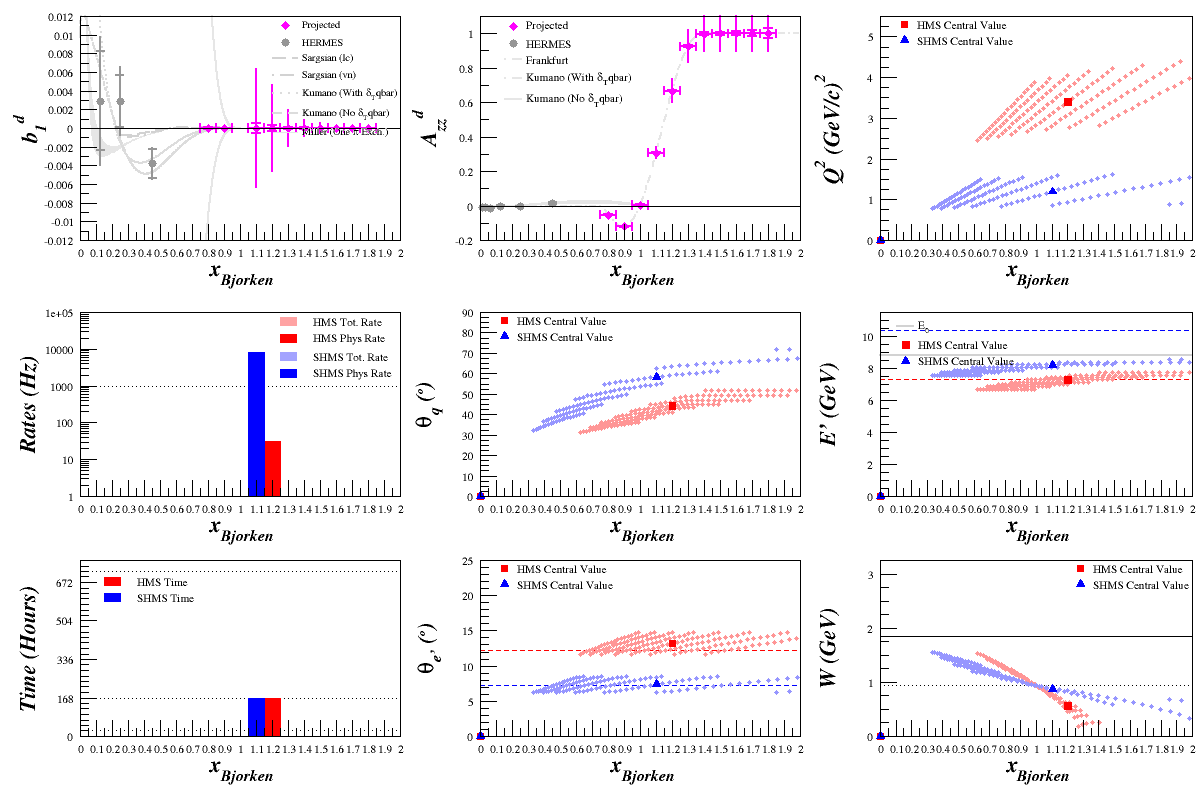
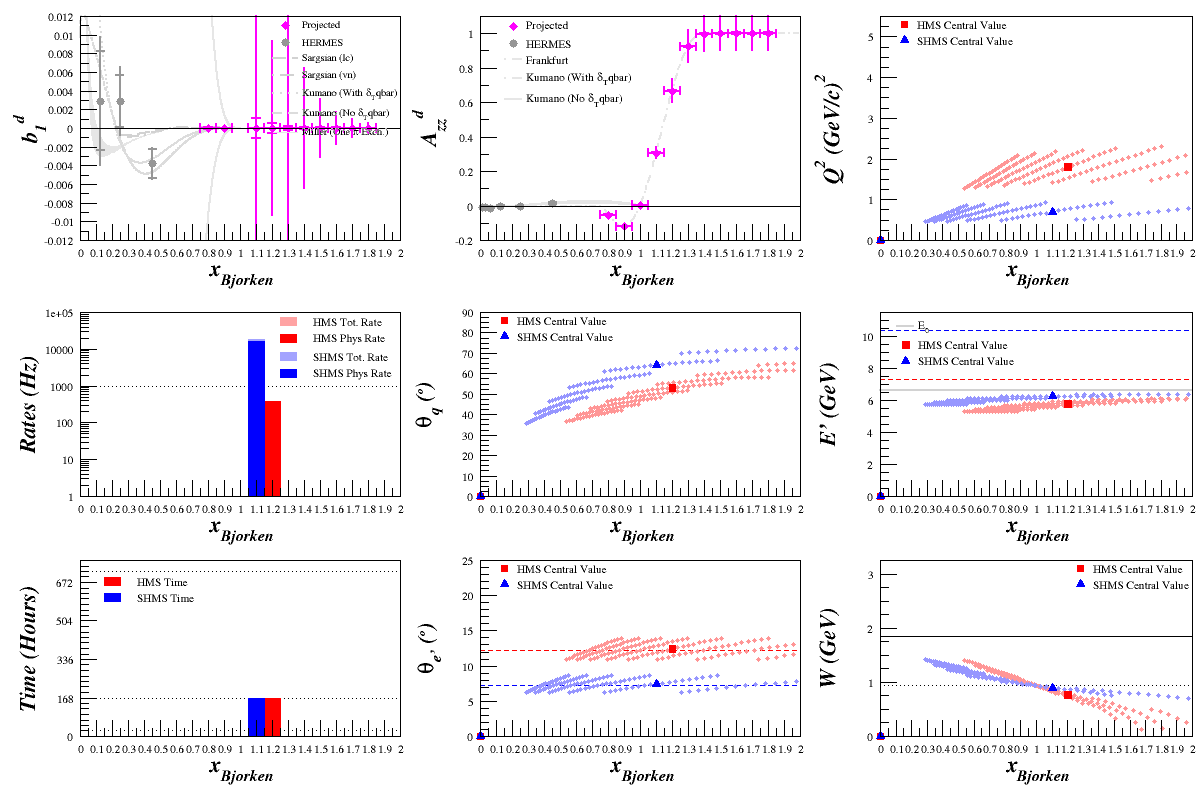
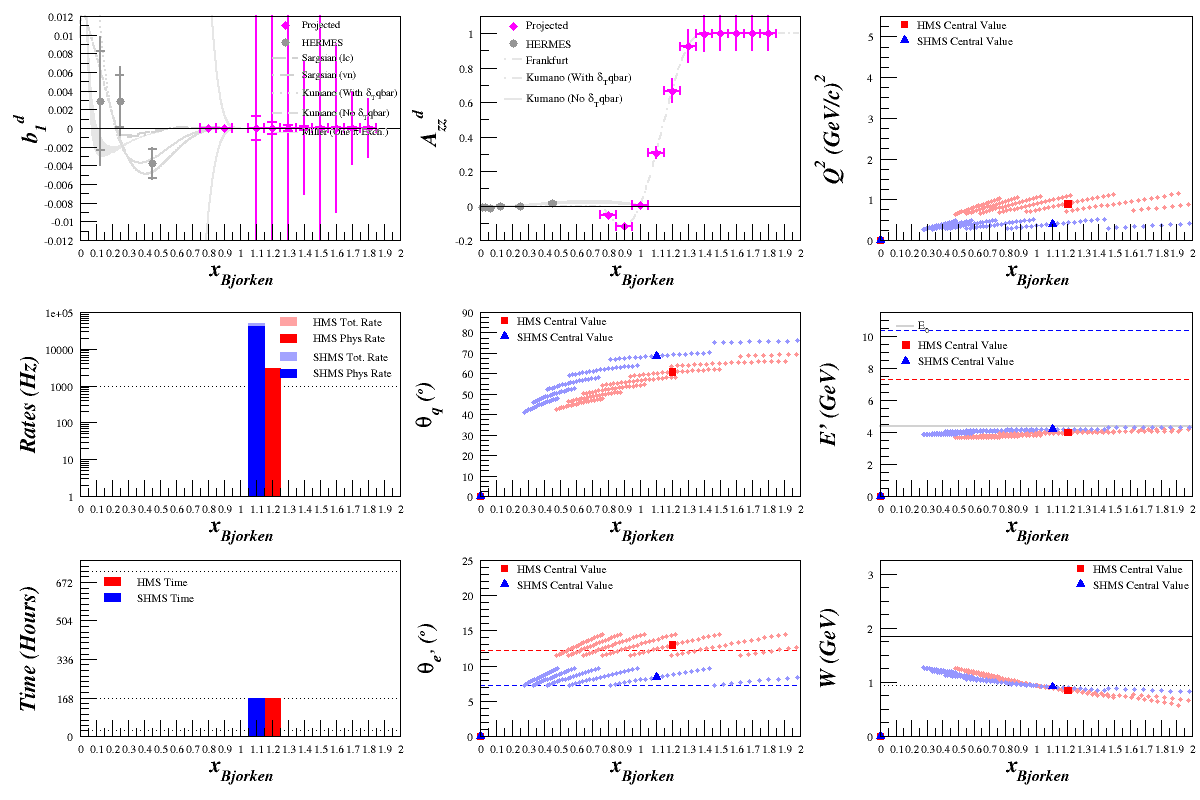
Beam Energy = 11.0 GeV
HMS
SHMS
Optimization Results
Beam Energy = 2.2 GeV
Beam Energy = 4.4 GeV
Beam Energy = 6.6 GeV
Beam Energy = 8.8 GeV
Beam Energy = 11.0 GeV
(None for HMS -- rates drop off dramatically by the time it's in a good kinematics range)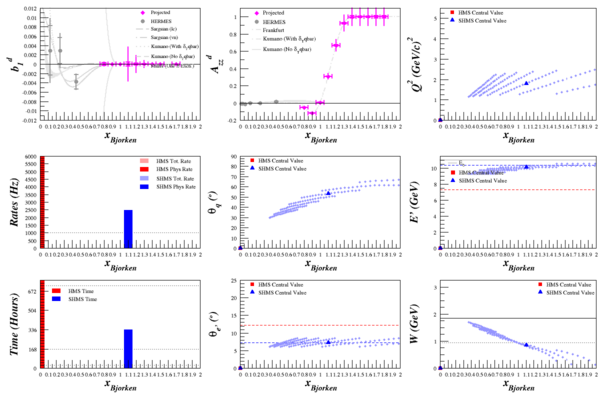
Fixed uncertainty due to large asymmetry
Previously, the code was using a simplified <math>\delta A_{zz} = \frac{4}{f \cdot Pzz \sqrt{N}}</math>. This gave all of the above uncertainties, as well as this one:
Going back through the uncertainty tech note, the assumption of a small asymmetry isn't made until after Eq. 28. Utilizing the full uncertainty (Eq. 28 and 25), <math>\delta A_{zz} = \frac{2}{f \cdot Pzz}\sqrt{\frac{N_{Pol}}{N_u^2}+\frac{N_{Pol}^2}{N_u^3}}</math>, the uncertainties change (very slightly) to:
Time Scan
Scanning over time and increasing it from 1 day to 2 weeks in intervals of one day, we get:
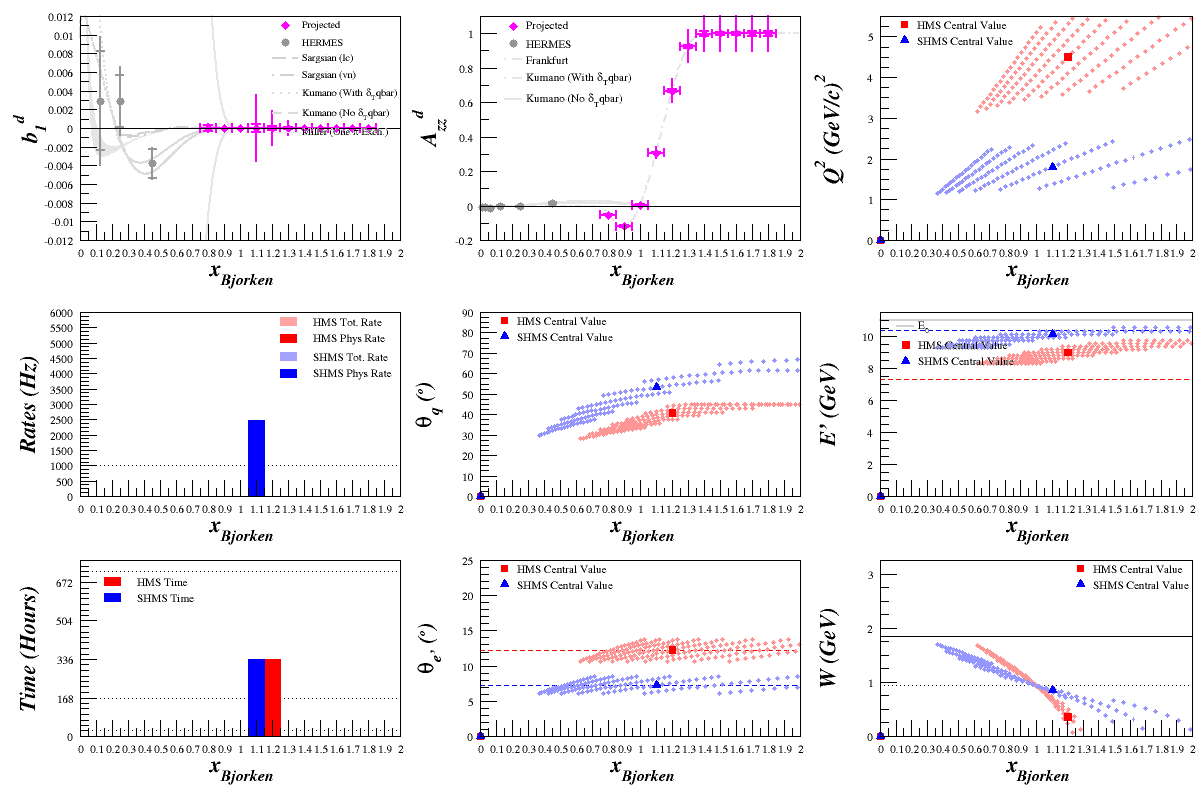
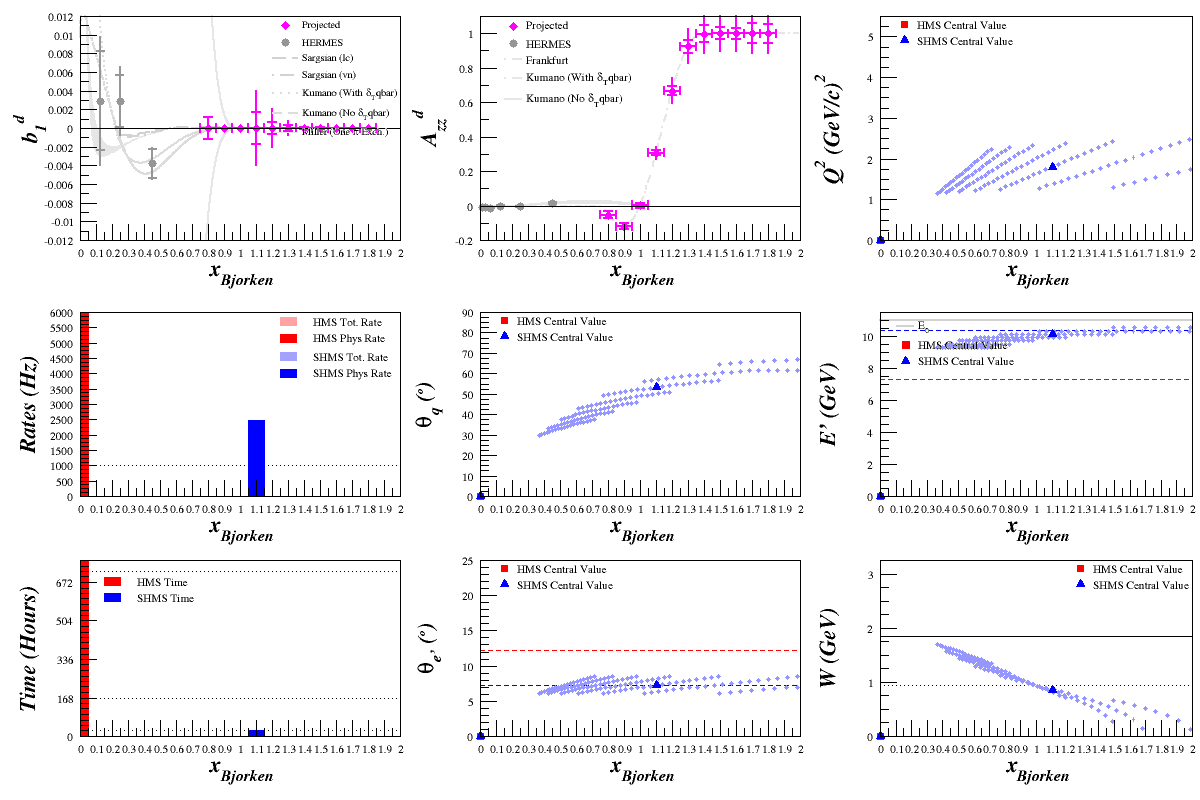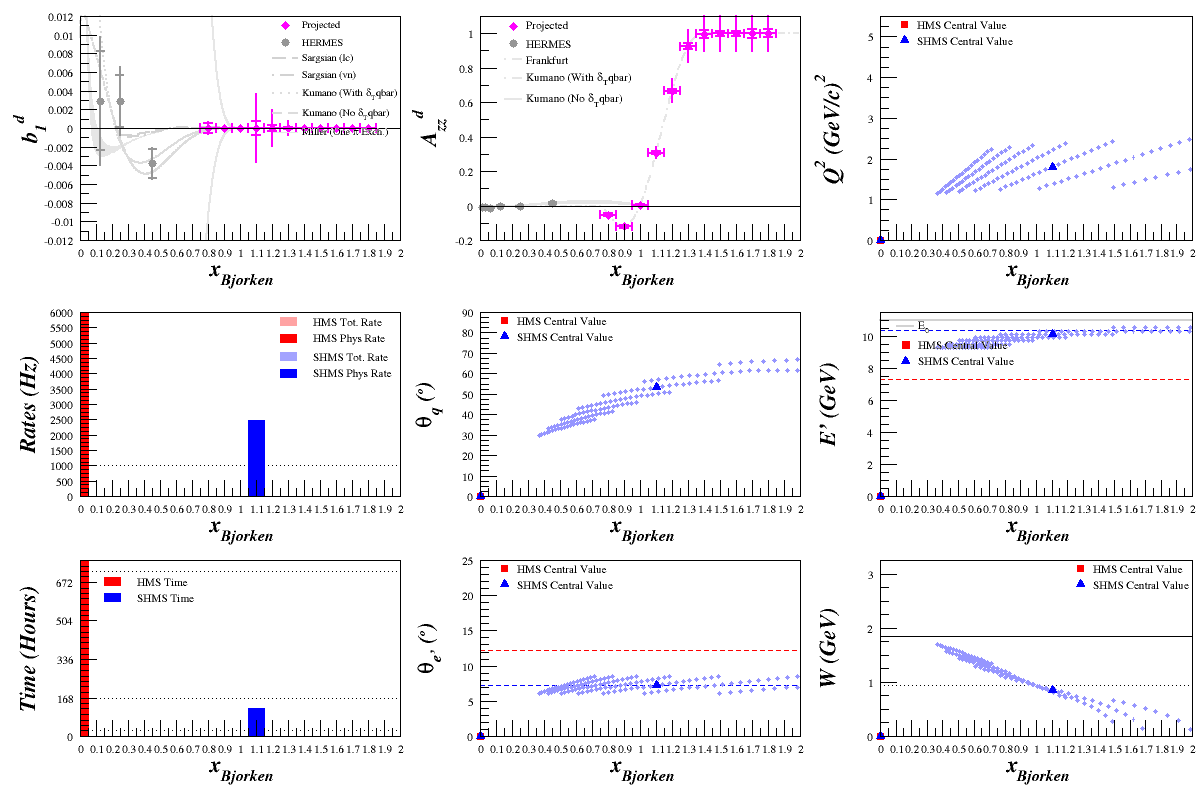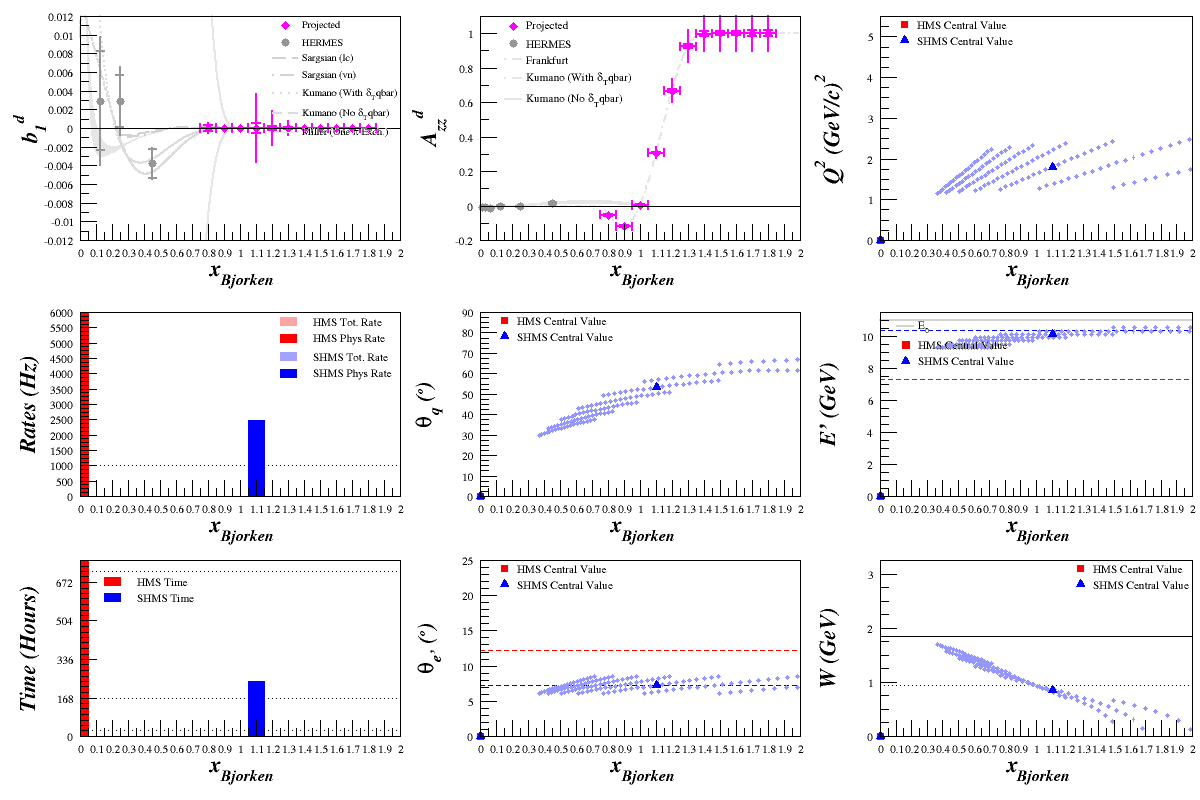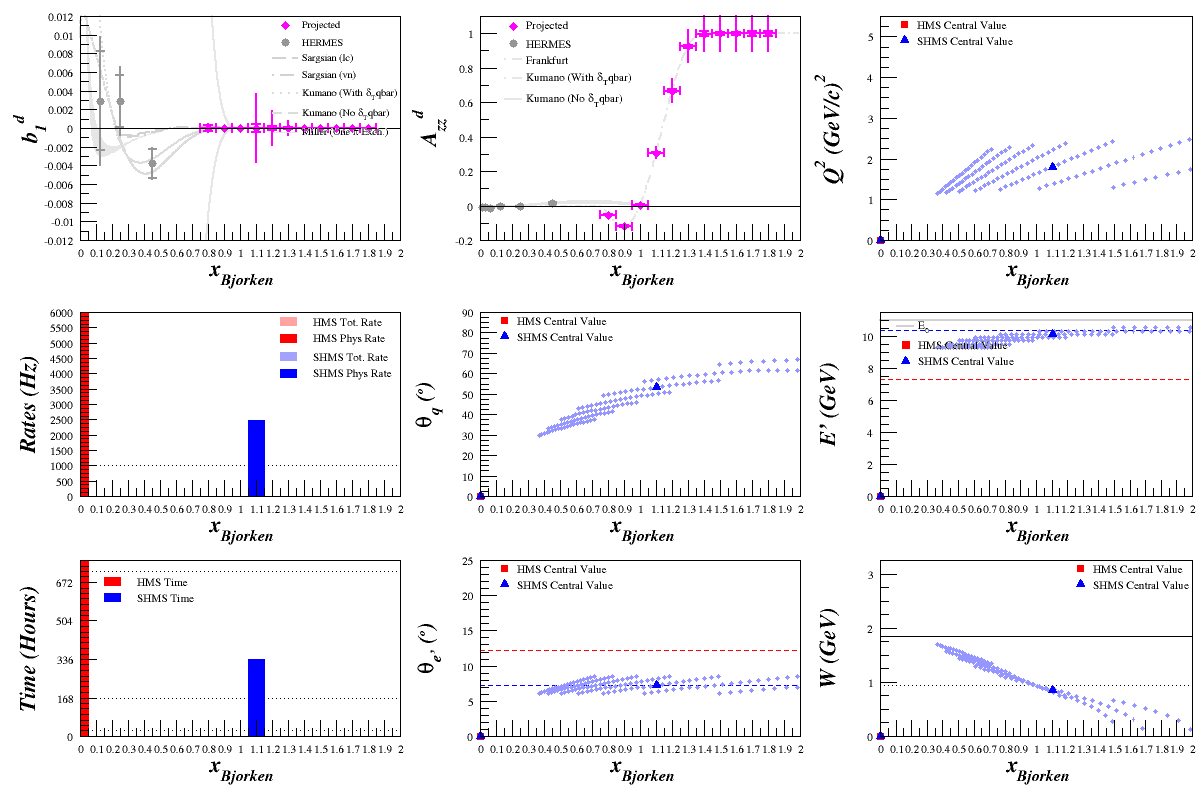
1 Week Measurement
Given one PAC week, using the SHMS and an 11 GeV beam on an 30% tensor polarized target, we can expect to get a good measurement from <math>0.8 > x > 1.8</math>
Beam Energy = 11.0 GeV
Beam Energy = 8.8 GeV
Beam Energy = 6.6 GeV
Beam Energy = 4.4 GeV
Beam Energy = 2.2 GeV
--E. Long 21:13, 19 September 2013 (UTC)