Elong-15-04-07
Relating t20 and Azz
The Boden '91 paper, the only existing t20 measurement taken with a solid ND3 target, does a nice job of describing the relationship between the measured ratio and t20. Eq. 1 describes their ratio,
<math>R_{exp}=\frac{d\sigma_p}{d\sigma_u}=1+P_{zz} \left( \frac{d\sigma_T-d\sigma_u}{d\sigma_u} \right) = 1+P_{zz} \left( R_T-1 \right) </math>
<math>R_T-1 = \frac{1}{P_{zz}} \left( \frac{d\sigma_p}{d\sigma_u} -1 \right).</math>
This matches closely to our Azz,
<math>A_{zz}=\frac{2}{fP_{zz}}\left( \frac{d\sigma_p}{d\sigma_u}-1\right), </math>
where the <math>f=1</math> in the Boden result, since they are tagging deuterons and have negligible contamination.
The two are related by
<math>R_T-1=\frac{1}{2}A_{zz}.</math>
Later on in the paper, <math>(R_T-1)</math> is related to t20 by neglecting the (small) magnetic contributions to get
<math>t_{20}=-\sqrt{8}(R_T-1),</math>
which we can relate to our Azz above by
<math>t_{20}=-\sqrt{2}A_{zz}.</math>
Adjusting the uncertainties calculated last week, which were simply Azz at x=2, by
<math>\delta t_{20} = \sqrt{2}\delta A_{zz},</math>
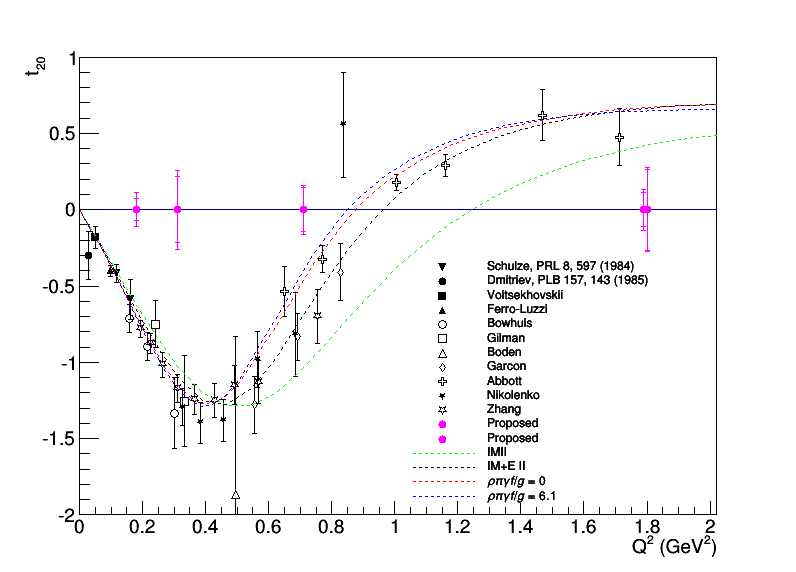
we get the plot below. Note that we can easily decrease the statistical (inner) uncertainty on the lowest Q^2 points, especially if we want to use it as a calibration.
An important caveat related to the first topic above: The Boden measurement tags deuterons with a hadron scattering angle of ~70 deg, which is where each t20 measurement was taken or rotated to on the plot above. We should be able to do the same inclusively by making a kinematic cut on the elastic peak. I'm looking into (but haven't finished) putting the HRS in position to tag deuterons, which would allow us to decrease DAQ rate and thus go to lower Q^2 with higher statistics in less time, at least for the lowest Q^2 point which we can use to calibrate the rest.