Elong-15-05-07

Going back through the literature, the NIKHEF measurements (for instance the Bouwhuis measurement) define the polarized D(e,e'd) cross section as

<math>\sigma = \sigma_0\left[ 1 + \frac{A_d^T P_{zz}}{\sqrt{2}} \right]</math>

where

<math> A^T_d = \sum_{i=0}^{2}d_{2i}T_{2i}</math>

and

<math> d_{20} = \frac{3 \cos^2 \theta^* -1}{2},~~d_{21} = -\sqrt{\frac{3}{2}}\sin2\theta^*\cos\phi^*,~~d_{22}=\sqrt{\frac{3}{2}}\sin^2\theta^*\cos 2\phi^*</math>

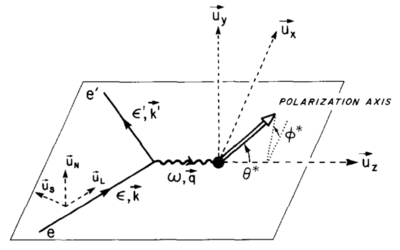
where <math>\theta^*</math> and <math>\phi^*</math> are in the frame where the <math>z</math> axis is along the <math>\vec{q}</math> (which for us is ~70deg from the beamline) and the <math>x</math> axis is perpendicular to <math>z</math> in the scattering plane. They take the same definitions given by Donnely and Raskin:

If I'm understanding that correctly, then for us <math>\theta^* = \theta_q = 70^{\circ}</math> and <math>\phi^* = 0^{\circ}</math> since our magnetic field will be oriented along the beamline.

If that's the case, the <math>d_{21}\approx -0.787,~~d_{22}\approx 1.08~~</math> and <math>d_{20} \approx -0.3245</math>.

Rearranging their top equation to get to what we measure as <math>A_{zz} = \frac{2}{P_{zz}}\left( \frac{\sigma}{\sigma_0} - 1 \right)</math>,

<math>A_{zz} = \sqrt{2}\left[ \frac{\sqrt{2}}{P_{zz}}\left( \frac{\sigma}{\sigma_0}-1\right) \right] = \left[ (-0.3245) T_{20} -0.787 T_{21} + 1.08 T_{22}\right] \sqrt{2}</math>

<math> A_{zz} = -0.458 T_{20} - 1.113T_{21} + 1.53T_{22}</math>.

The error from this would propagate to

<math> \delta T_{20}^{stat} = 2.18\cdot \delta A_{zz}^{stat}</math>

<math> \delta T_{20}^{sys} =\sqrt{ \left(2.18\cdot \delta A_{zz}^{sys}\right)^2 + \left(2.42\cdot\delta T_{21}\right)^2 + \left(3.33\cdot\delta T_{22}\right)^2 }</math>.

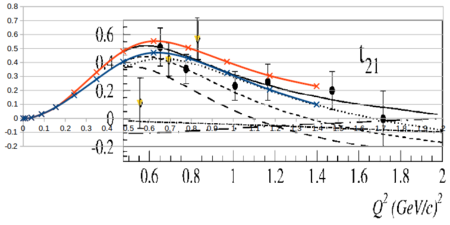
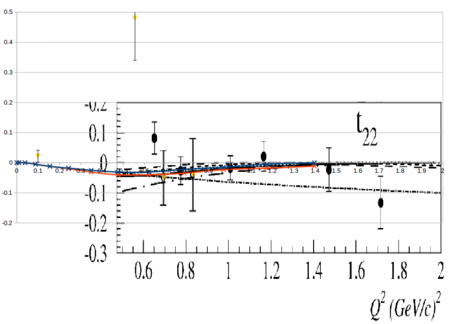
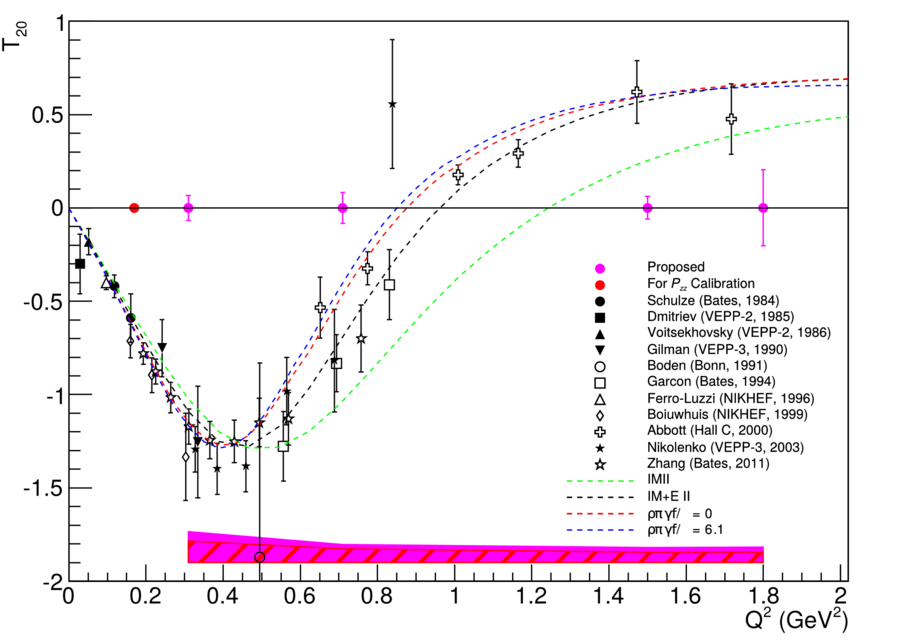
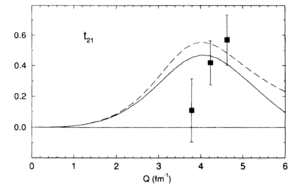
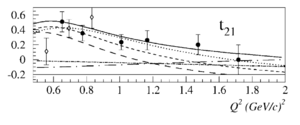
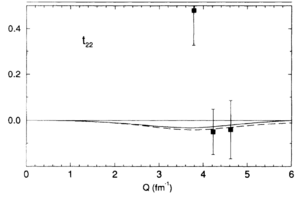
Looking at the world data for <math>T_{21}</math> and <math>T_{22}</math>,

Garcon (1992)	Ferro-Luzzi (1996)	Abbott (2000)

Overlaying the plots on top of each other so they both read in GeV² looks like

In discussions with Doug, a reasonable uncertainty on T21 and T22 would be 10%. This was included in the systematics band, along with systematics from Azz, and is shown below.