One of the major sources of background in the proposed setting that facilitates detection of very forward particles is electrons associated with bremsstrahlung process. During the E89-009 experiment, data was taken with a lead sheet blocking 0 degree bremsstrahlung electrons just at the entrance of the Enge spectrometer. It was learned that blocking 0 degree bremsstrahlung electrons improves considerably signal to noise ratio. The ``Tilt method'' offers greater hypernuclear yield by more than an order of magnitude and better signal to noise ratio by a factor of 10 compared to the E89-009 setup.
Electron rates at the focal plane of the Enge spectrometer were estimated
as given in table 10
for a beam current of 30 ![]() A and a target thickness of 100 mg/cm
A and a target thickness of 100 mg/cm![]() .
When the ``Tilt method'' is employed, the bremsstrahlung electron rate
is estimated to be less than 1 MHz
for a beam intensity of 30
.
When the ``Tilt method'' is employed, the bremsstrahlung electron rate
is estimated to be less than 1 MHz
for a beam intensity of 30 ![]() A.
This rate is much less than
a few times 100 MHz observed during E89-009.
A.
This rate is much less than
a few times 100 MHz observed during E89-009.
We assume the integrated singles rate of the electron arm as 1 MHz for the estimation of signal to accidental background ratio. The kaon singles rate of the HKS spectrometer was estimated to be 380 Hz for the carbon target as shown in table 10. With a coincidence window of 2 ns in the off-line analysis, the accidental coincidence rate in the final spectrum will be:
Assuming that the accidental coincidence events are spread uniformly
over the energy matrix (Enge 190 MeV ![]() HKS 270 MeV),
the accidental background rate per bin (100 keV) projected on the hypernuclear
mass spectrum can be estimated to be:
HKS 270 MeV),
the accidental background rate per bin (100 keV) projected on the hypernuclear
mass spectrum can be estimated to be:
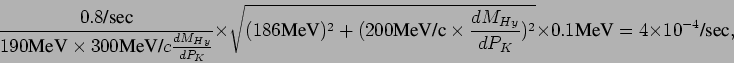
where
![]() is the kaon momentum dependence of the
hypernuclear energy; 186 MeV and 200 MeV/
is the kaon momentum dependence of the
hypernuclear energy; 186 MeV and 200 MeV/![]() are coming from
the
are coming from
the ![]() B(g.s.) position
in energy matrix (see figure 7).
B(g.s.) position
in energy matrix (see figure 7).
A typical hypernuclear (![]() C target) event rate will be
33 / (100 nb/sr) / h = 9.2
C target) event rate will be
33 / (100 nb/sr) / h = 9.2
![]() / (100 nb/sr) / sec
as shown in table 5.
The cross section of
/ (100 nb/sr) / sec
as shown in table 5.
The cross section of ![]() B(g.s.) doublet was measured as
140 nb/sr in E89-009.
Therefore signal to noise ratio can be estimated assuming the ground state
peaks are distributed in 3 bins (300 keV):
B(g.s.) doublet was measured as
140 nb/sr in E89-009.
Therefore signal to noise ratio can be estimated assuming the ground state
peaks are distributed in 3 bins (300 keV):
| Target |
 |
 |
 |
|
|
30 | 33 | 380 |
|
|
30 | 14 | 320 |
|
|
30 | 8 | 290 |