Difference between revisions of "Elong-13-09-12"
| (2 intermediate revisions by the same user not shown) | |||
| Line 16: | Line 16: | ||
| − | Each of these points, with an uncertainty of ±0.01 on account of my estimating from a previous work without direct points, was then put into a graph in ROOT and fit with a 6th-order polynomial, | + | Each of these points, with an uncertainty of ±0.01 on account of my estimating from a previous work without direct points, was then put into a graph in ROOT and fit with a 6th-order polynomial, $\sum_{n=0}^6w_n\cdot x^n$ |
[[Image:2013-09-12-fs-Azz-fit.png|800px]] | [[Image:2013-09-12-fs-Azz-fit.png|800px]] | ||
:::{| class="wikitable" style="text-align:center; border-collapse:collapse;" border="1" | :::{| class="wikitable" style="text-align:center; border-collapse:collapse;" border="1" | ||
| − | | style="width: 20px;" | | + | | style="width: 20px;" | $n$ || style="width: 200px;" | $w_n$ |
|- | |- | ||
| 0 || -5.68296e+01 ± 1.22251e-02 | | 0 || -5.68296e+01 ± 1.22251e-02 | ||
| Line 43: | Line 43: | ||
---- | ---- | ||
| − | Starting with x=0.5, 0.75, 1.0, and 1.25 and including the Frankfurt and Strikman plot for Azz in the Quasi-Elastic range, I scanned over the spectrometers' center Q^2 values, looking for the best rates that fall within the spectrometers' limits. (All plots assume Pzz=35%) | + | Starting with x=0.5, 0.75, 1.0, and 1.25 (using the code described in [http://nuclear.unh.edu/~elong/analysis_files/2013-05-16/Azz_error.pdf the rates technote]) and including the Frankfurt and Strikman plot for Azz in the Quasi-Elastic range, I scanned over the spectrometers' center Q^2 values, looking for the best rates that fall within the spectrometers' limits. (All plots assume Pzz=35%) |
[[Image:2013-09-13-shms_x_050.gif]] | [[Image:2013-09-13-shms_x_050.gif]] | ||
Latest revision as of 13:53, 18 October 2023
Adding QE Range
Frankfurt and Strikman's 1988 Azz
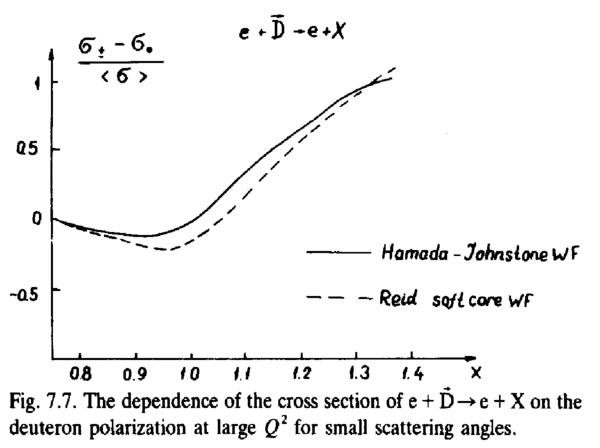
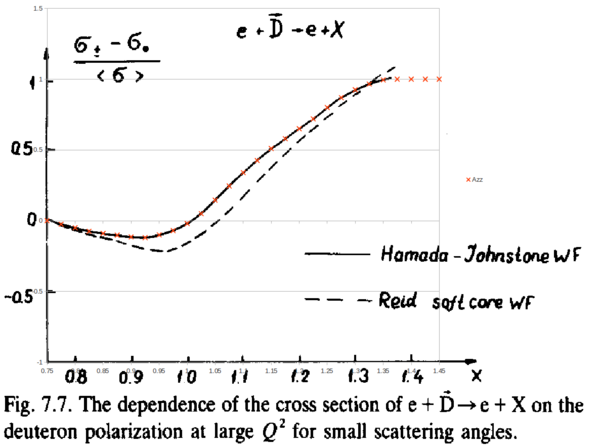
In their 1988 report on Hard Nuclear Processes and Microscopic Structure, Fig. 7.7 plots what appears to be Azz.
I took this plot and super-imposed it onto a plot in a spreadsheet so that I could estimate points along the curve.
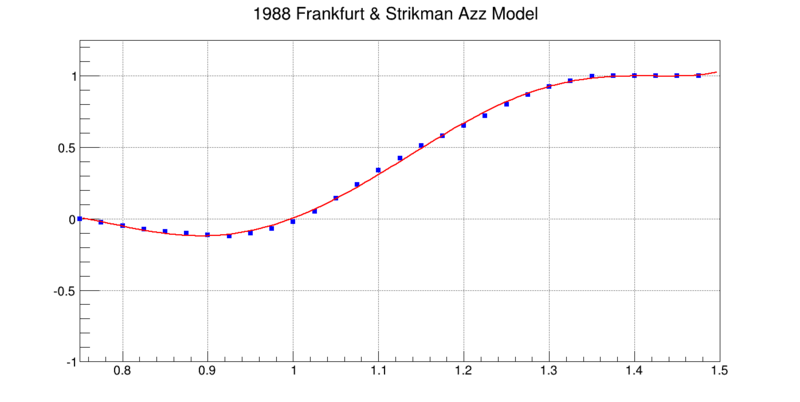
Each of these points, with an uncertainty of ±0.01 on account of my estimating from a previous work without direct points, was then put into a graph in ROOT and fit with a 6th-order polynomial, $\sum_{n=0}^6w_n\cdot x^n$
$n$ $w_n$ 0 -5.68296e+01 ± 1.22251e-02 1 2.46102e+02 ± 1.66137e-02 2 -3.51484e+02 ± 1.39410e-02 3 1.11641e+02 ± 1.11237e-02 4 1.63698e+02 ± 8.63783e-03 5 -1.48174e+02 ± 6.15266e-03 6 3.50491e+01 ± 3.63922e-03
This fit was written up as a subroutine for the b1 rates code. It also assumes that at x>1.425, Azz=1 and that at x<0.75, Azz=0. The b1 rates code was then updated to use the previous Kumano curves for x<0.75 and this new QE curve for x>=0.75.
Q2 Scan
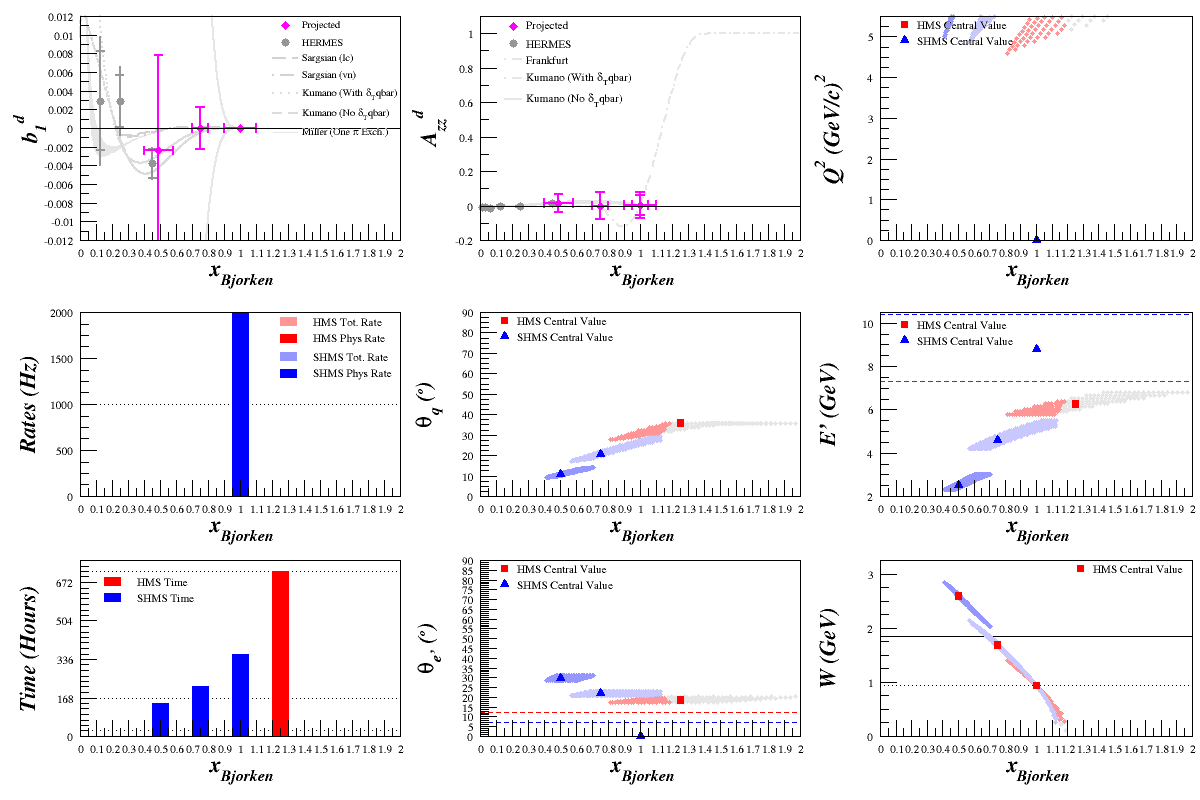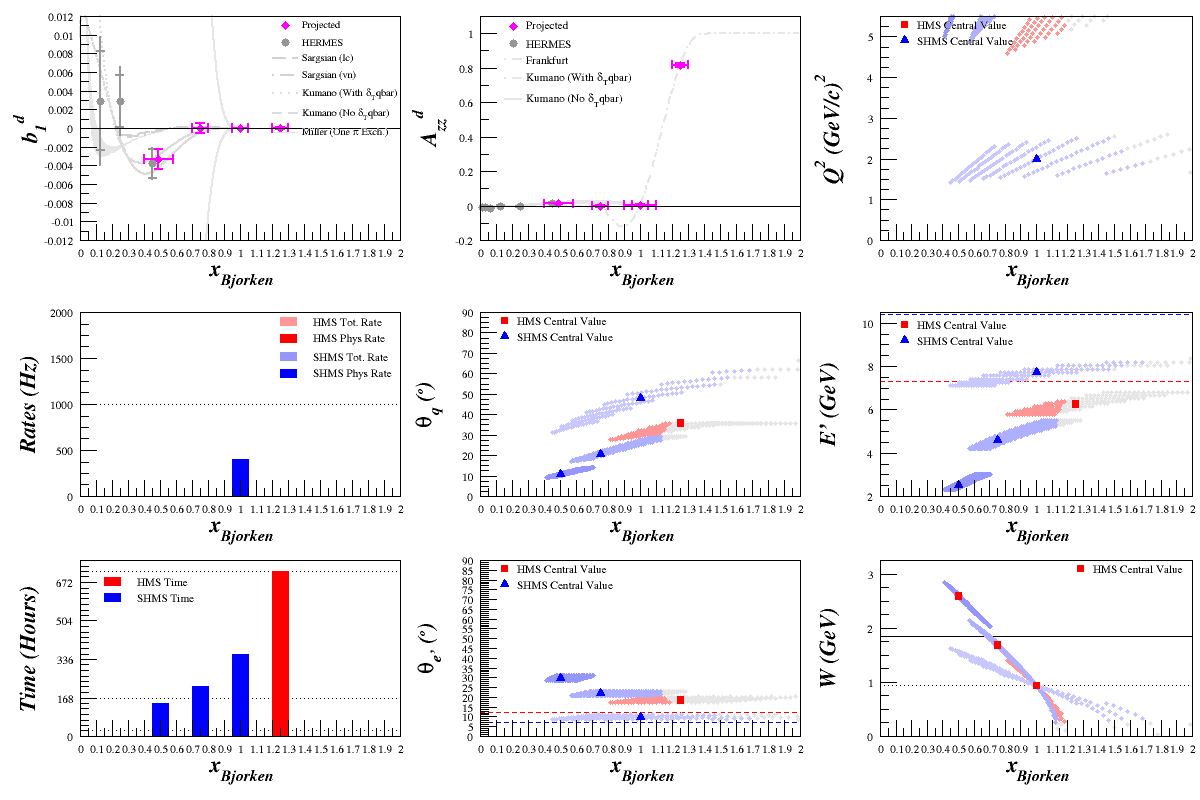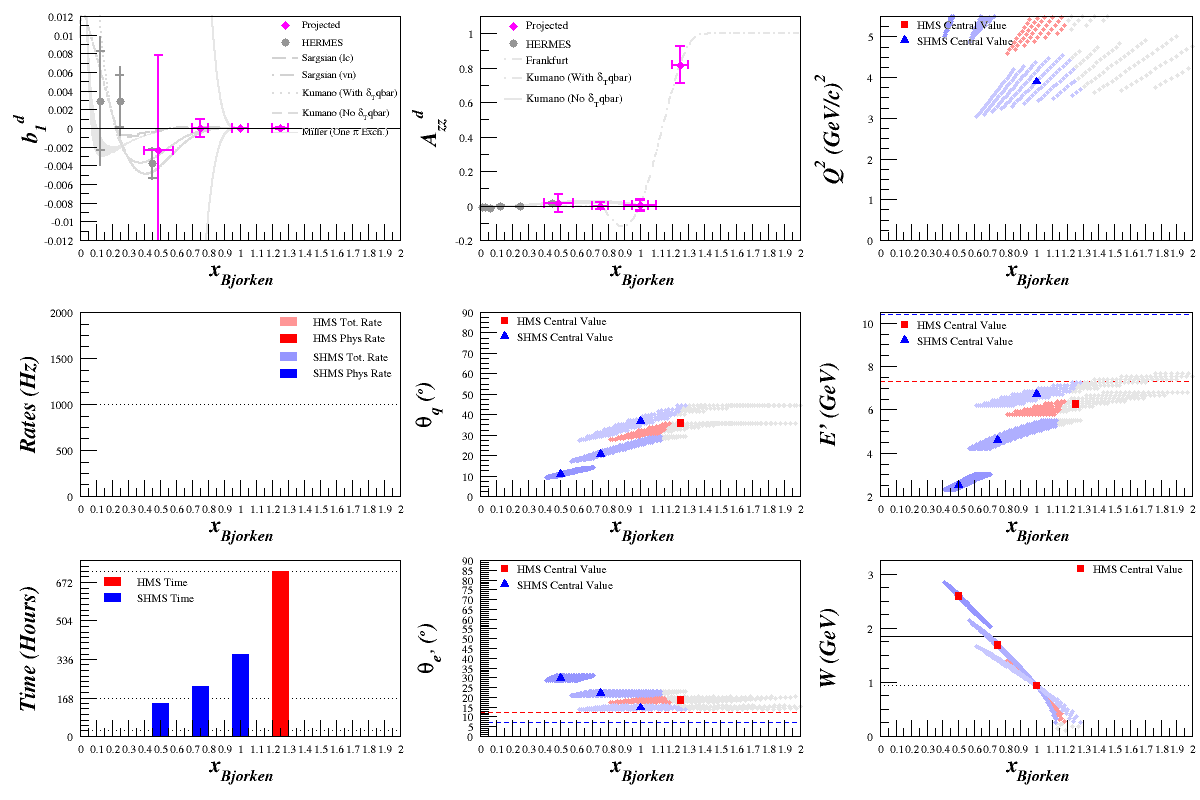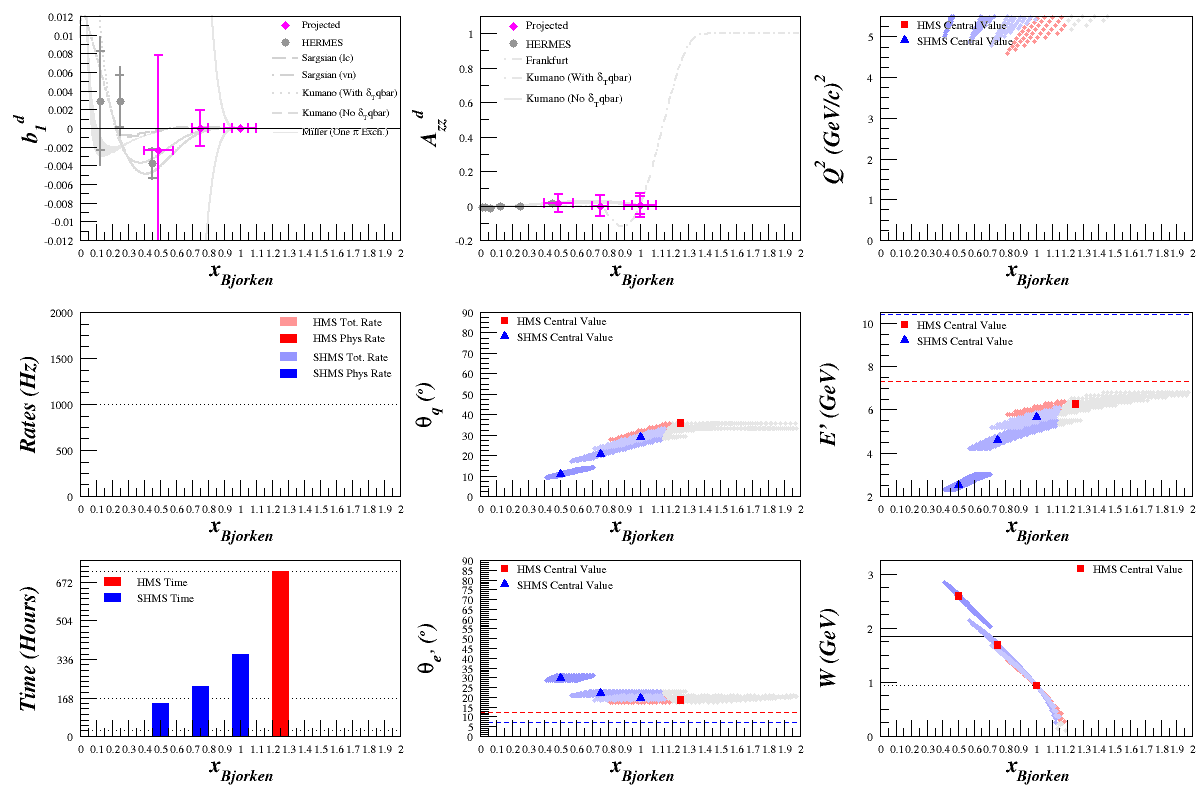
Starting with x=0.5, 0.75, 1.0, and 1.25 (using the code described in the rates technote) and including the Frankfurt and Strikman plot for Azz in the Quasi-Elastic range, I scanned over the spectrometers' center Q^2 values, looking for the best rates that fall within the spectrometers' limits. (All plots assume Pzz=35%)
First Pass Results
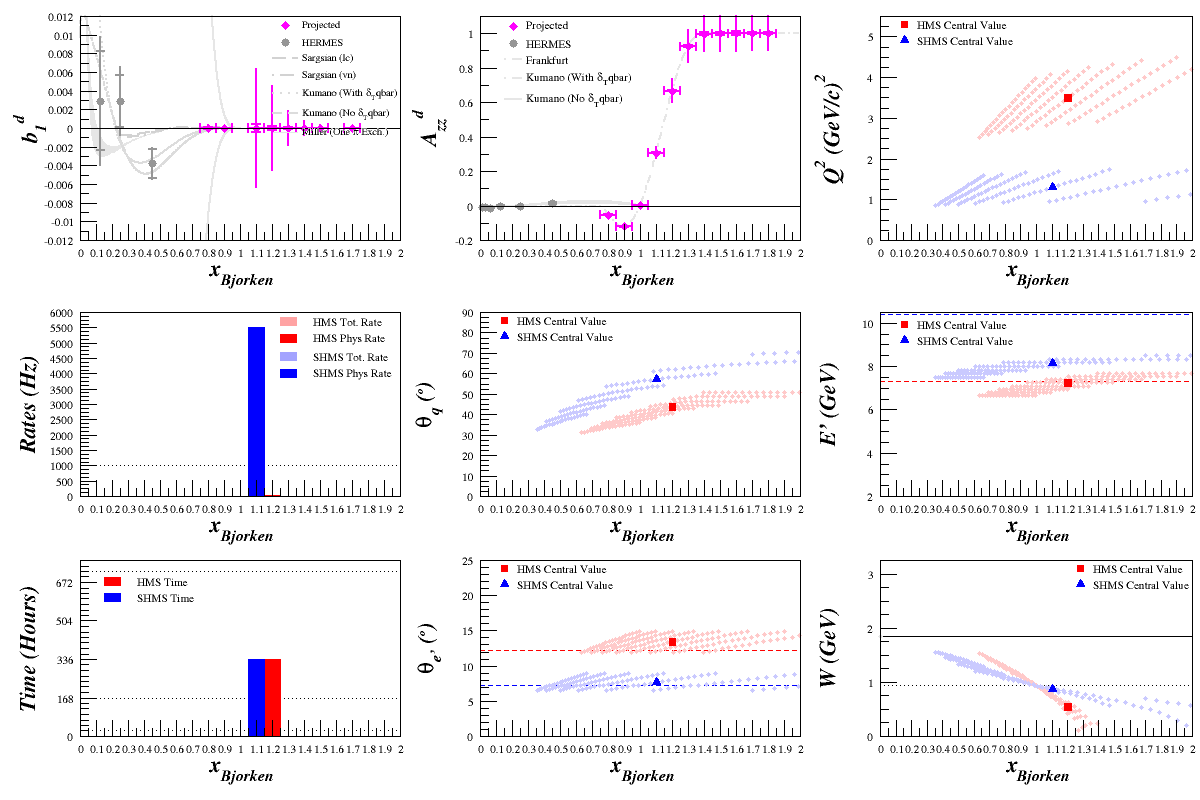
This is still a work in progress (for example, the lowest x point in b1 moves a bit which is caused by fluctuations in F1 moving from inelastic to quasi-elastic scattering in calculating the point) and I'll be continuing to look at different x points to perhaps make a smoother transition, especially where Azz goes from near-zero to very large values. But at the moment, here's a rates estimate for a potential measurement:
HMS Q2 Scan
HMS Q2 Scan
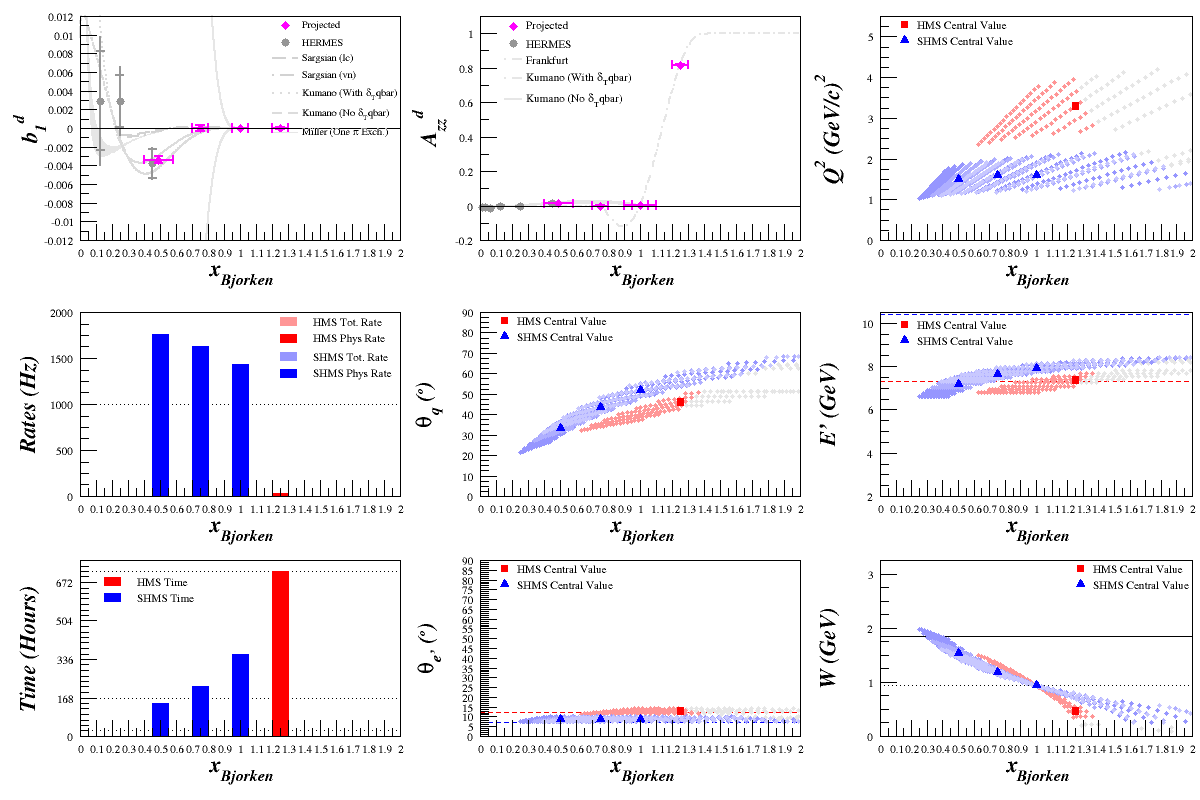
Single Setting, 2 Week Measurement
First attempt at extending the number of rebinned events in x and putting the SHMS and the HMS at a single setting for two weeks. Still need to include the fact that the large asymmetry uncertainty isn't included (currently 1/sqrt(N), not applicable as Azz>>0) and double-check that the cross sections match what I expect in the QE region. The majority of the uncertainty comes from an estimated 10% (relative to Azz) systematic that's now been included, figuring that'll about be what the polarimetry uncertain is.
--E. Long 22:10, 13 September 2013 (UTC)