Difference between revisions of "Elong-15-05-04"
From HallCWiki
Jump to navigationJump to search| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
The deuteron elastic peak was calculated using a [[Elong-15-02-26 | parametrization of the deuteron elastic form factors A and B]] by | The deuteron elastic peak was calculated using a [[Elong-15-02-26 | parametrization of the deuteron elastic form factors A and B]] by | ||
| − | + | $ | |
\frac{d^2 \sigma}{d\Omega dE'} = \sigma_{\mathrm{Mott}}\left(\frac{E'}{E}\right)\left[ A + B \tan ^2 \left( \frac{\theta}{2} \right) \right] \delta (E'-E'_{el}), | \frac{d^2 \sigma}{d\Omega dE'} = \sigma_{\mathrm{Mott}}\left(\frac{E'}{E}\right)\left[ A + B \tan ^2 \left( \frac{\theta}{2} \right) \right] \delta (E'-E'_{el}), | ||
| − | + | $ | |
| − | where | + | where $\delta(E'-E'_{el})$ is approximated by a Gaussian distribution with its width determined by the resolution of the spectrometers, |
| − | + | ||
| + | $ | ||
\delta(E'-E'_{el}) = \frac{1}{2\Delta E\cdot E'_{el}\sqrt{\pi}}e^{-\frac{(E'-E'_{el})^2}{2(\Delta E\cdot E'_{el})^2}}, | \delta(E'-E'_{el}) = \frac{1}{2\Delta E\cdot E'_{el}\sqrt{\pi}}e^{-\frac{(E'-E'_{el})^2}{2(\Delta E\cdot E'_{el})^2}}, | ||
| − | + | $ | |
| − | where | + | where $\Delta E=0.1 ~(0.08)\%$ for the HMS (SHMS) and $E'_{el}=\frac{Q^2}{2m_D}.$ |
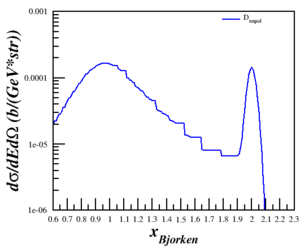
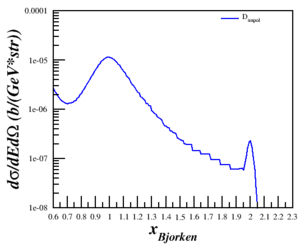
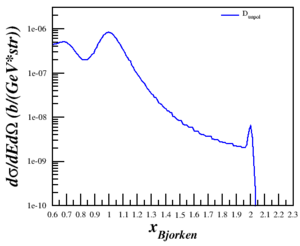
Results of the cross section vs. x are shown below for three Q<sup>2</sup>. | Results of the cross section vs. x are shown below for three Q<sup>2</sup>. | ||
{| border="1" style="text-align:center;" | {| border="1" style="text-align:center;" | ||
| − | ! | + | ! $Q^2 = 0.17$ (GeV<sup>2</sup>) !! $Q^2 = 0.71$ (GeV<sup>2</sup>) !! $Q^2 = 1.50$ (GeV<sup>2</sup>) |
|- | |- | ||
| [[Image:2015-05-06-sig-q2-017.png|300px]] || [[Image:2015-05-06-sig-q2-071.png|300px]] || [[Image:2015-05-06-sig-q2-0150.png|300px]] | | [[Image:2015-05-06-sig-q2-017.png|300px]] || [[Image:2015-05-06-sig-q2-071.png|300px]] || [[Image:2015-05-06-sig-q2-0150.png|300px]] | ||
|- | |- | ||
|} | |} | ||
Latest revision as of 14:31, 18 October 2023
The deuteron elastic peak was calculated using a parametrization of the deuteron elastic form factors A and B by
$ \frac{d^2 \sigma}{d\Omega dE'} = \sigma_{\mathrm{Mott}}\left(\frac{E'}{E}\right)\left[ A + B \tan ^2 \left( \frac{\theta}{2} \right) \right] \delta (E'-E'_{el}), $
where $\delta(E'-E'_{el})$ is approximated by a Gaussian distribution with its width determined by the resolution of the spectrometers,
$ \delta(E'-E'_{el}) = \frac{1}{2\Delta E\cdot E'_{el}\sqrt{\pi}}e^{-\frac{(E'-E'_{el})^2}{2(\Delta E\cdot E'_{el})^2}}, $
where $\Delta E=0.1 ~(0.08)\%$ for the HMS (SHMS) and $E'_{el}=\frac{Q^2}{2m_D}.$
Results of the cross section vs. x are shown below for three Q2.
| $Q^2 = 0.17$ (GeV2) | $Q^2 = 0.71$ (GeV2) | $Q^2 = 1.50$ (GeV2) |
|---|---|---|
 |
 |
|