Elong-15-05-04
From HallCWiki
Jump to navigationJump to searchThe deuteron elastic peak was calculated using a parametrization of the deuteron elastic form factors A and B by
$ \frac{d^2 \sigma}{d\Omega dE'} = \sigma_{\mathrm{Mott}}\left(\frac{E'}{E}\right)\left[ A + B \tan ^2 \left( \frac{\theta}{2} \right) \right] \delta (E'-E'_{el}), $
where $\delta(E'-E'_{el})$ is approximated by a Gaussian distribution with its width determined by the resolution of the spectrometers,
$ \delta(E'-E'_{el}) = \frac{1}{2\Delta E\cdot E'_{el}\sqrt{\pi}}e^{-\frac{(E'-E'_{el})^2}{2(\Delta E\cdot E'_{el})^2}}, $
where $\Delta E=0.1 ~(0.08)\%$ for the HMS (SHMS) and $E'_{el}=\frac{Q^2}{2m_D}.$
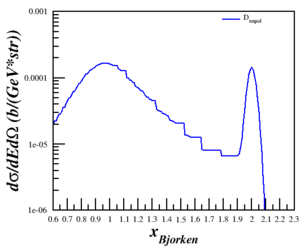
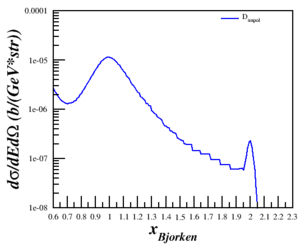
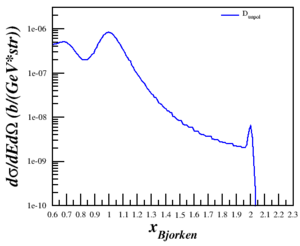
Results of the cross section vs. x are shown below for three Q2.
| $Q^2 = 0.17$ (GeV2) | $Q^2 = 0.71$ (GeV2) | $Q^2 = 1.50$ (GeV2) |
|---|---|---|
 |
 |
|