Elong-15-04-30

Background

As mentioned previously, I was able to calculate the elastic cross section using a parameterization of the deuteron's elastic form factors. With the A and B form factors, the cross section was estimated as

<math>\sigma = \sigma_{Mott} \left[ A + B \tan^2 \left( \frac{\theta}{2} \right) \right]</math>

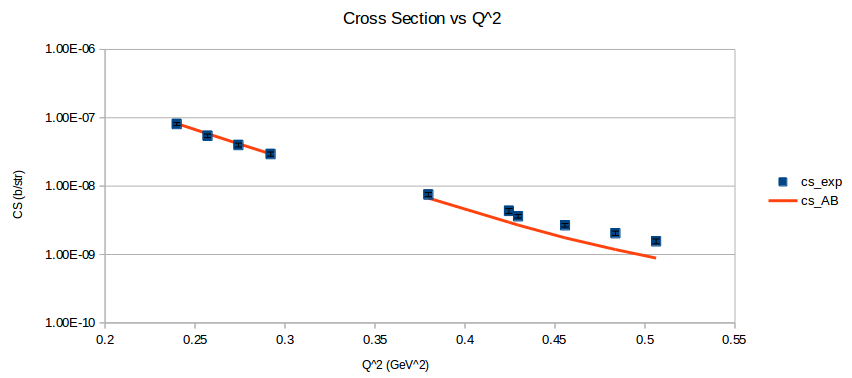
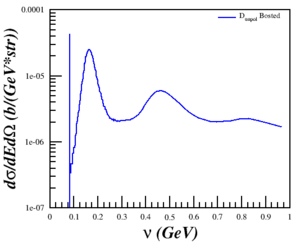
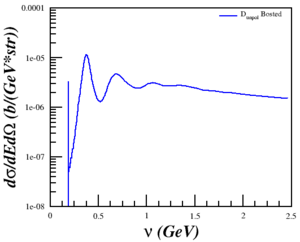
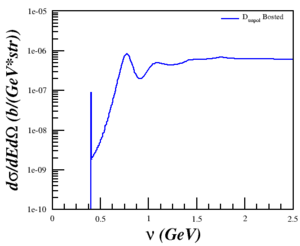
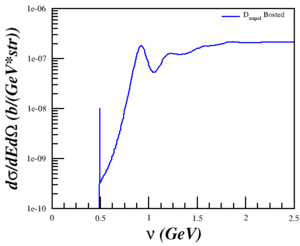
I found a paper from Galster (1971) that included elastic cross sections (and not just A and B), which I was able to reproduce well. (Note: The dip around Q2=0.5 is because of the parameterization underestimating A.)

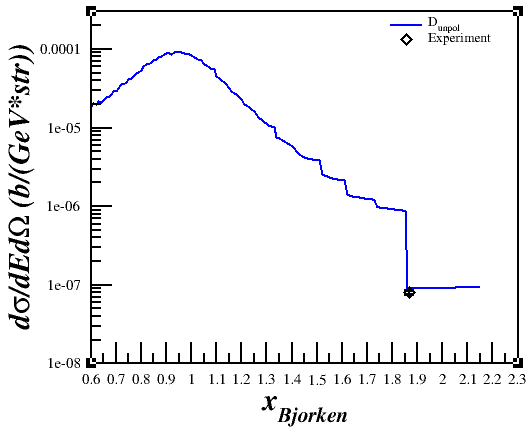
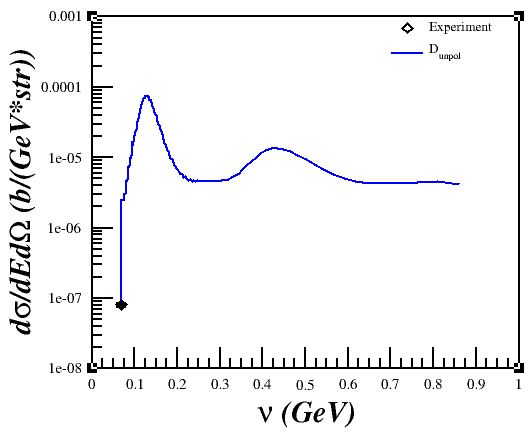
However, when I would plot it versus x or nu,

I wasn't getting what I was expecting in relation to the QE peak.

The Fix

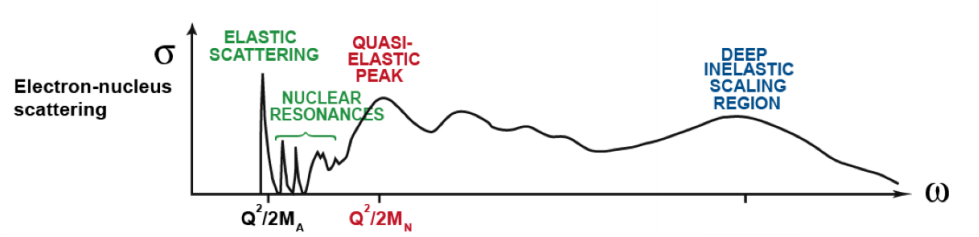
Discussing the issue with Doug and Donal, I realized that the problem was that I was trying to compare a single-derivative elastic cross section with a double-derivative QE cross section, so what I was plotting was the area of the elastic peak and not the peak itself. This was fixed by using a delta function, estimated as <math>\delta(E'-E'_{el}) \approx \frac{n}{\sqrt{\pi}}e^{-n^2 (E'-E'_{el})^2}</math> with <math>n = 5000</math> and <math>E'_{el}=\frac{Q^2}{(2M_D)}</math>, to the cross section. Now, the cross section is calculated by

<math>\sigma = \sigma_{Bosted} + \sigma_{elastic}</math>

where

<math>\sigma_{elastic} = \sigma_{Mott} \left[ A + B \tan^2 \left( \frac{\theta}{2} \right) \right]\delta(E'-E'_{el})</math>

behaves as expected.

<math>Q^2 = 0.18</math> (GeV2)	<math>Q^2 = 0.31</math> (GeV2)	<math>Q^2 = 0.71</math> (GeV2)	<math>Q^2 = 1.50</math> (GeV2)	<math>Q^2 = 1.80</math> (GeV2)