Difference between revisions of "Elong-15-04-30"
| Line 35: | Line 35: | ||
|- | |- | ||
|} | |} | ||
| + | |||
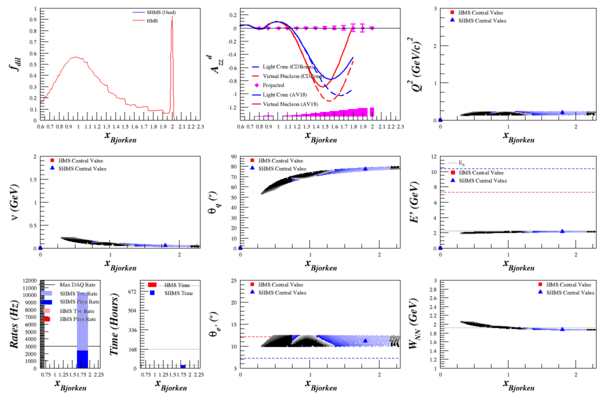
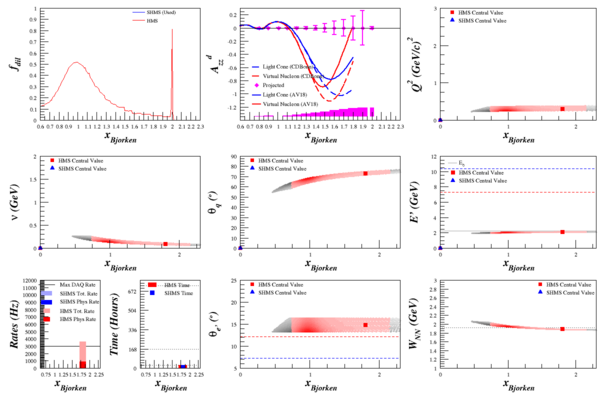
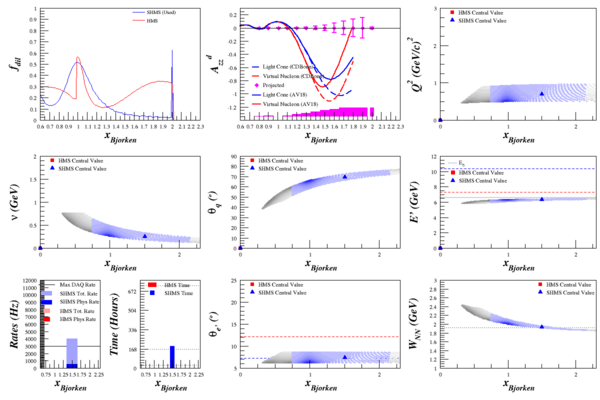
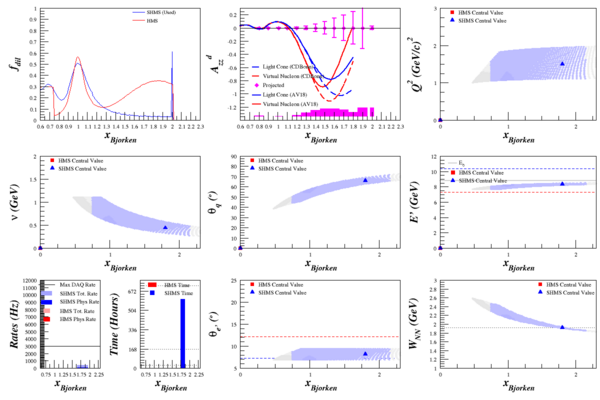
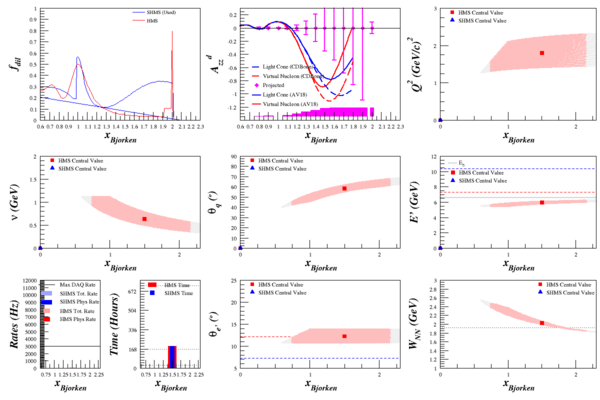
| + | =The Rates= | ||
| + | |||
| + | My rates code requires double-derivative <math>\frac{d^2\sigma}{d\Omega d\E'}</math> to work, as it algebraically integrates over small bins in <math>\Omega</math> and <math>E'</math>. Running this through the rates code allowed me to calculate elastic <math>A_{zz}</math>, which has significantly smaller uncertainty from its QE neighbors due to the spike in the dilution factor. | ||
| + | |||
| + | [[Image:2015-04-30-azz-q2-018.png|600px]] | ||
| + | |||
| + | [[Image:2015-04-30-azz-q2-031.png|600px]] | ||
| + | |||
| + | [[Image:2015-04-30-azz-q2-071.png|600px]] | ||
| + | |||
| + | [[Image:2015-04-30-azz-q2-150.png|600px]] | ||
| + | |||
| + | [[Image:2015-04-30-azz-q2-180.png|600px]] | ||
Revision as of 12:56, 30 April 2015
Background
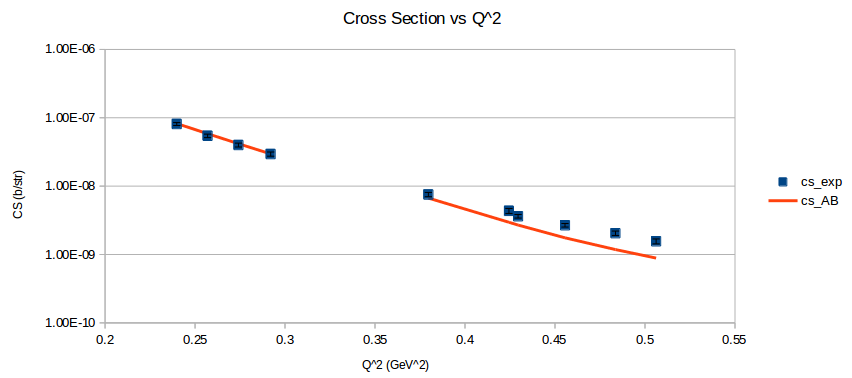
As mentioned previously, I was able to calculate the elastic cross section using a parameterization of the deuteron's elastic form factors. With the A and B form factors, the cross section was estimated as
<math>\sigma = \sigma_{Mott} \left[ A + B \tan^2 \left( \frac{\theta}{2} \right) \right]</math>
I found a paper from Galster (1971) that included elastic cross sections (and not just A and B), which I was able to reproduce well. (Note: The dip around Q2=0.5 is because of the parameterization underestimating A.)
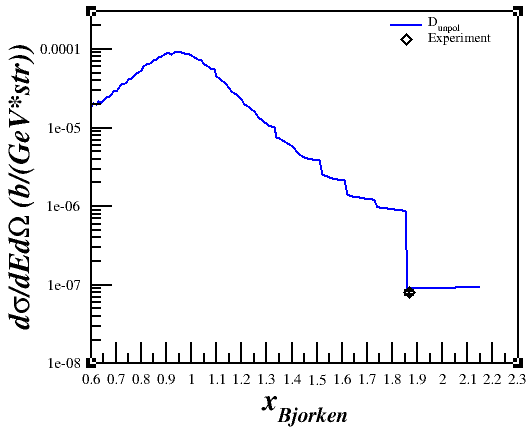
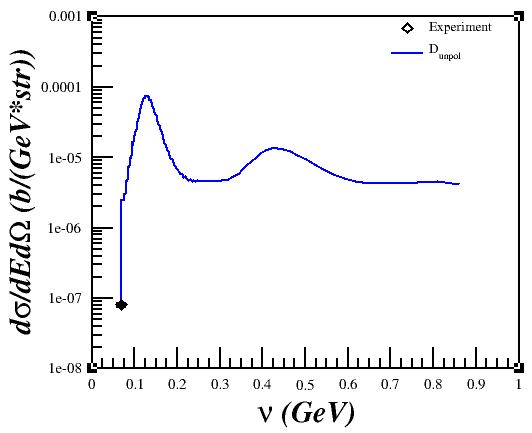
However, when I would plot it versus x or nu,
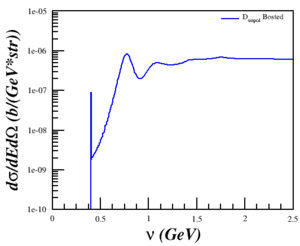
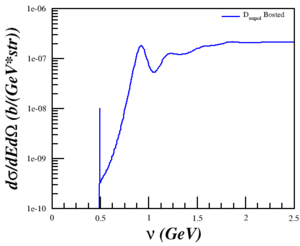
I wasn't getting what I was expecting in relation to the QE peak.
The Fix
Discussing the issue with Doug and Donal, I realized that the problem was that I was trying to compare a single-derivative elastic cross section with a double-derivative QE cross section, so what I was plotting was the area of the elastic peak and not the peak itself. This was fixed by using a delta function, estimated as <math>\delta(E'-E'_{el}) \approx \frac{n}{\sqrt{\pi}}e^{-n^2 (E'-E'_{el})^2}</math> with <math>n = 5000</math> and <math>E'_{el}=\frac{Q^2}{(2M_D)}</math>, to the cross section. Now, the cross section is calculated by
<math>\sigma = \sigma_{Bosted} + \sigma_{elastic}</math>
where
<math>\sigma_{elastic} = \sigma_{Mott} \left[ A + B \tan^2 \left( \frac{\theta}{2} \right) \right]\delta(E'-E'_{el})</math>
behaves as expected.
| <math>Q^2 = 0.18</math> (GeV2) | <math>Q^2 = 0.31</math> (GeV2) | <math>Q^2 = 0.71</math> (GeV2) | <math>Q^2 = 1.50</math> (GeV2) | <math>Q^2 = 1.80</math> (GeV2) |
|---|---|---|---|---|
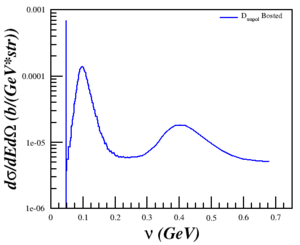 |
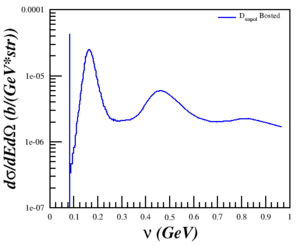 |
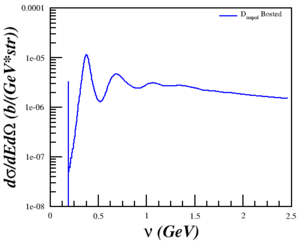 |
 |
|
The Rates
My rates code requires double-derivative <math>\frac{d^2\sigma}{d\Omega d\E'}</math> to work, as it algebraically integrates over small bins in <math>\Omega</math> and <math>E'</math>. Running this through the rates code allowed me to calculate elastic <math>A_{zz}</math>, which has significantly smaller uncertainty from its QE neighbors due to the spike in the dilution factor.