Lower HMS Angle
In going back through some of the Azz work done recently, it occurred to me that since we'll be operating in a longitudinal field for the target, that we might be able to go to a lower angle with the HMS and those bring in more statistics. In particular, the minimum angle between the spectrometers is 17.5 degrees, and the absolute lowest the HMS can go is 10.5 degrees. I played around a bit pushing the kinematics to balance that against the maximum E' of 7.30 GeV (Pzz=30 for all plots):

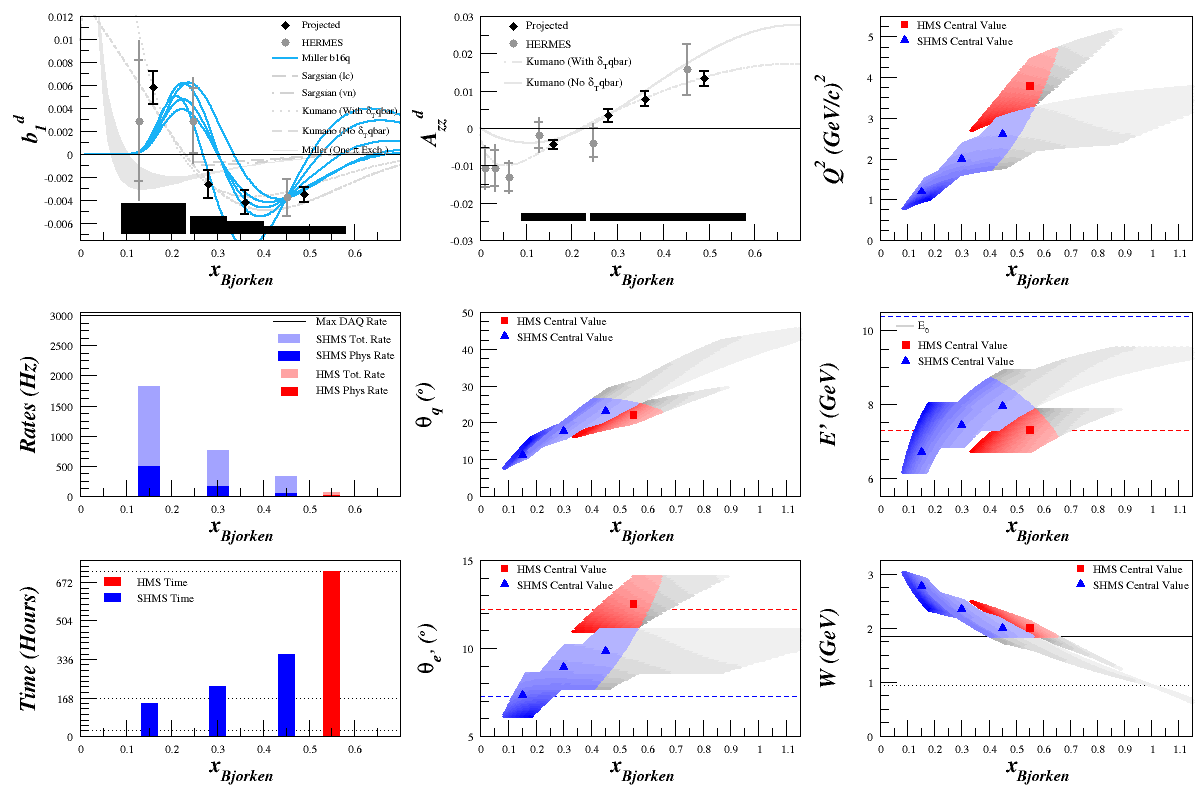
If we can push the HMS, we can improve our uncertainties (both statistical and systematic, since systematic depends on statistical):
Proposal HMS Settings
$\theta_{e'}=12.52^{\circ}$
$E'=7.30\mathrm{~GeV}$ |
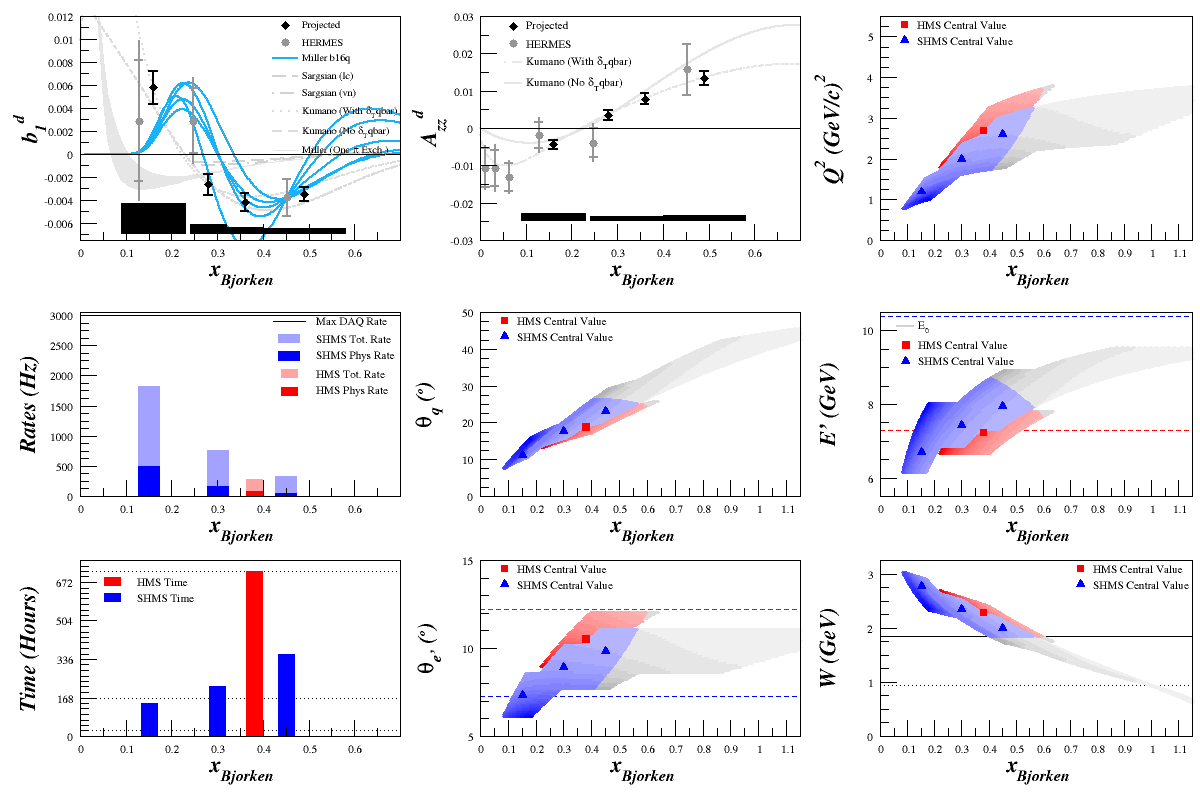
Updated HMS Settings
$\theta_{e'}=10.52^{\circ}$
$E'=7.24\mathrm{~GeV}$
|
| $\delta b_1^{stat} (x=0.16) = 0.144\times 10^{-2}$ |
$\delta b_1^{sys} (x=0.16) = 0.272\times 10^{-2}$ |
$\delta b_1^{stat} (x=0.16) = 0.143\times 10^{-2}$ |
$\delta b_1^{sys} (x=0.16) = 0.270\times 10^{-2}$
|
| $\delta b_1^{stat} (x=0.28) = 0.123\times 10^{-2}$ |
$\delta b_1^{sys} (x=0.28) = 0.156\times 10^{-2}$ |
$\delta b_1^{stat} (x=0.28) = 0.924\times 10^{-3}$ |
$\delta b_1^{sys} (x=0.28) = 0.899\times 10^{-3}$
|
| $\delta b_1^{stat} (x=0.36) = 0.102\times 10^{-2}$ |
$\delta b_1^{sys} (x=0.36) = 0.116\times 10^{-2}$ |
$\delta b_1^{stat} (x=0.36) = 0.756\times 10^{-3}$ |
$\delta b_1^{sys} (x=0.36) = 0.674\times 10^{-3}$
|
| $\delta b_1^{stat} (x=0.49) = 0.637\times 10^{-3}$ |
$\delta b_1^{sys} (x=0.49) = 0.711\times 10^{-3}$ |
$\delta b_1^{stat} (x=0.49) = 0.613\times 10^{-3}$ |
$\delta b_1^{sys} (x=0.49) = 0.556\times 10^{-3}$
|
 |
|


