Difference between revisions of "Elong-15-05-06"
| Line 3: | Line 3: | ||
The [http://link.springer.com/article/10.1007%2FBF01555492 Boden '91 paper], the only existing t20 measurement taken with a solid ND3 target, does a nice job of describing the relationship between the measured ratio and t20. Eq. 1 describes their ratio, | The [http://link.springer.com/article/10.1007%2FBF01555492 Boden '91 paper], the only existing t20 measurement taken with a solid ND3 target, does a nice job of describing the relationship between the measured ratio and t20. Eq. 1 describes their ratio, | ||
| − | + | $R_{exp}=\frac{d\sigma_p}{d\sigma_u}=1+P_{zz} \left( \frac{d\sigma_T-d\sigma_u}{d\sigma_u} \right) = 1+P_{zz} \left( R_T-1 \right) $ | |
| − | + | $R_T-1 = \frac{1}{P_{zz}} \left( \frac{d\sigma_p}{d\sigma_u} -1 \right).$ | |
This matches closely to our Azz, | This matches closely to our Azz, | ||
| − | + | $A_{zz}=\frac{2}{fP_{zz}}\left( \frac{d\sigma_p}{d\sigma_u}-1\right), $ | |
| − | where the | + | where the $f=1$ in the Boden result, since they are tagging deuterons and have negligible contamination. |
The two are related by | The two are related by | ||
| − | + | $R_T-1=\frac{1}{2}A_{zz}.$ | |
| − | Later on in the paper, | + | Later on in the paper, $(R_T-1)$ is related to t20 by neglecting the (small) magnetic contributions to get |
| − | + | $t_{20}=-\sqrt{8}(R_T-1),$ | |
which we can relate to our Azz above by | which we can relate to our Azz above by | ||
| − | + | $t_{20}=-\sqrt{2}A_{zz}.$ | |
[[Elong-15-04-30 | Calculating the elastic Azz at x=2]] and [[Elong-15-05-04 | smearing the elastic peak using the spectrometers' momentum resolution]] to use in the dilution factor calculation, we can relate the uncertainty in t20 to Azz by | [[Elong-15-04-30 | Calculating the elastic Azz at x=2]] and [[Elong-15-05-04 | smearing the elastic peak using the spectrometers' momentum resolution]] to use in the dilution factor calculation, we can relate the uncertainty in t20 to Azz by | ||
| − | + | $\delta t_{20} = \sqrt{2}\delta A_{zz},$ | |
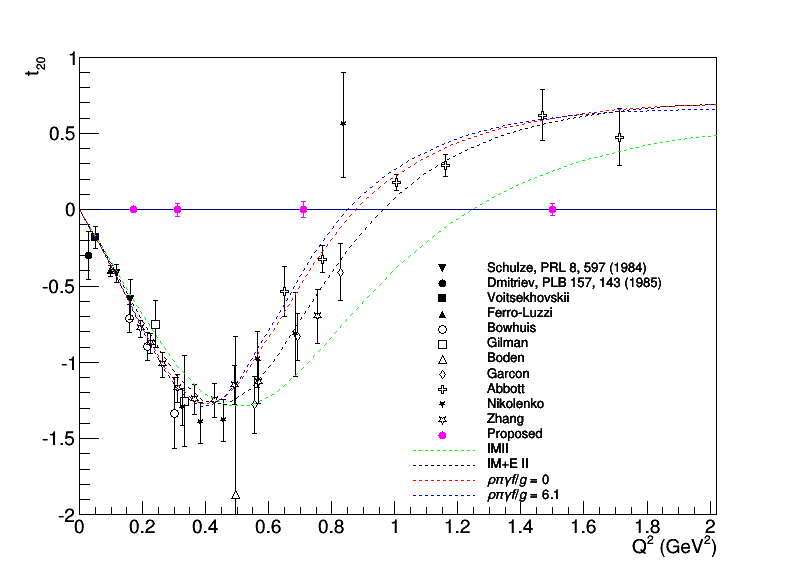
which yields the plot below of statistical uncertainty we would expect for longitudinally-tensor-polarized electron-deuteron scattering. | which yields the plot below of statistical uncertainty we would expect for longitudinally-tensor-polarized electron-deuteron scattering. | ||
[[Image:2015-05-06-t20-update.png]] | [[Image:2015-05-06-t20-update.png]] | ||
Latest revision as of 13:44, 18 October 2023
Relating t20 and Azz
The Boden '91 paper, the only existing t20 measurement taken with a solid ND3 target, does a nice job of describing the relationship between the measured ratio and t20. Eq. 1 describes their ratio,
$R_{exp}=\frac{d\sigma_p}{d\sigma_u}=1+P_{zz} \left( \frac{d\sigma_T-d\sigma_u}{d\sigma_u} \right) = 1+P_{zz} \left( R_T-1 \right) $
$R_T-1 = \frac{1}{P_{zz}} \left( \frac{d\sigma_p}{d\sigma_u} -1 \right).$
This matches closely to our Azz,
$A_{zz}=\frac{2}{fP_{zz}}\left( \frac{d\sigma_p}{d\sigma_u}-1\right), $
where the $f=1$ in the Boden result, since they are tagging deuterons and have negligible contamination.
The two are related by
$R_T-1=\frac{1}{2}A_{zz}.$
Later on in the paper, $(R_T-1)$ is related to t20 by neglecting the (small) magnetic contributions to get
$t_{20}=-\sqrt{8}(R_T-1),$
which we can relate to our Azz above by
$t_{20}=-\sqrt{2}A_{zz}.$
Calculating the elastic Azz at x=2 and smearing the elastic peak using the spectrometers' momentum resolution to use in the dilution factor calculation, we can relate the uncertainty in t20 to Azz by
$\delta t_{20} = \sqrt{2}\delta A_{zz},$
which yields the plot below of statistical uncertainty we would expect for longitudinally-tensor-polarized electron-deuteron scattering.