Elong-15-05-06
Relating t20 and Azz
The Boden '91 paper, the only existing t20 measurement taken with a solid ND3 target, does a nice job of describing the relationship between the measured ratio and t20. Eq. 1 describes their ratio,
$R_{exp}=\frac{d\sigma_p}{d\sigma_u}=1+P_{zz} \left( \frac{d\sigma_T-d\sigma_u}{d\sigma_u} \right) = 1+P_{zz} \left( R_T-1 \right) $
$R_T-1 = \frac{1}{P_{zz}} \left( \frac{d\sigma_p}{d\sigma_u} -1 \right).$
This matches closely to our Azz,
$A_{zz}=\frac{2}{fP_{zz}}\left( \frac{d\sigma_p}{d\sigma_u}-1\right), $
where the $f=1$ in the Boden result, since they are tagging deuterons and have negligible contamination.
The two are related by
$R_T-1=\frac{1}{2}A_{zz}.$
Later on in the paper, $(R_T-1)$ is related to t20 by neglecting the (small) magnetic contributions to get
$t_{20}=-\sqrt{8}(R_T-1),$
which we can relate to our Azz above by
$t_{20}=-\sqrt{2}A_{zz}.$
Calculating the elastic Azz at x=2 and smearing the elastic peak using the spectrometers' momentum resolution to use in the dilution factor calculation, we can relate the uncertainty in t20 to Azz by
$\delta t_{20} = \sqrt{2}\delta A_{zz},$
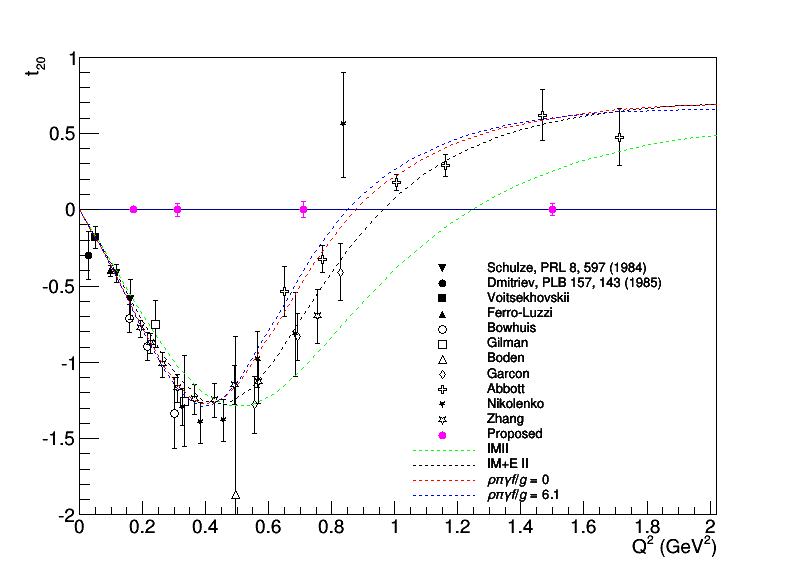
which yields the plot below of statistical uncertainty we would expect for longitudinally-tensor-polarized electron-deuteron scattering.